Engage NY Eureka Math Algebra 2 Module 3 Lesson 33 Answer Key
Eureka Math Algebra 2 Module 3 Lesson 33 Opening Exercise Answer Key
Opening Exercise:
In Problem 1 of the Problem Set of Lesson 32, you calculated the monthly payment for a 15-year mortgage at a 5% annual interest rate for the house you chose. You need that monthly payment to answer these questions.
a. About how much do you expect your home to be worth in 15 years?
Answer:
Answers will vary but should follow similar steps. For example:
Step 1: F = 190000(1.0295)15
Step 2: F ≈ 293866
My home will be worth about $294,000 if it continues to appreciate at an average rate of 2.95% every year.
b. For 0 ≤ x ≤ 15, plot the graph of the function f(x) = P(1 + r)x where r is the appreciation rate and P is the initial value of your home.
Answer:
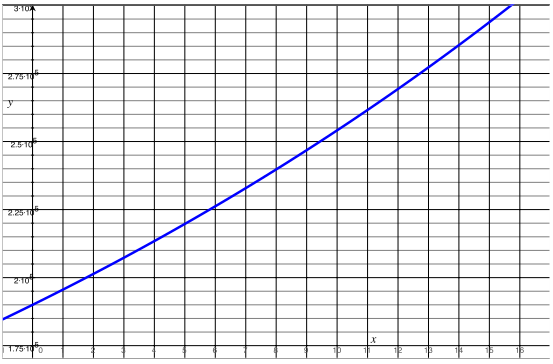
c. Compare the image of the graph you plotted in part (b) with a partner, and write your observations of the differences and similarities. What do you think is causing the differences that you see in the graphs? Share your observations with another group to see if your conclusions are correct.
Answer:
Answers will vary. Although the growth rate is the same for all students in the class, depending on the initial value of the home, different homes will appreciate more quickly than others. For instance, a house that is valued at $100,000 will increase to $154,666.15 in 15 years. This increase is about $49,000 less than the increase for a home with a $190,000 initial value.
The differences are caused by the differences in initial value. Since the rare of increase is a percentage and the home’s value increases exponentially, the increase is markedly different for more expensive homes and will be even more significant as years increase.
Your friend Julia bought a home at the same time as you but chose to finance the loan over 30 years. Julia also was able to avoid a down payment and financed the entire value of her home. This allowed her to purchase a more expensive home, but 15 years later she still has not paid off the loan. Consider the following amortization table representing Julia’s mortgage, and answer the following questions by comparing the table with your graph.
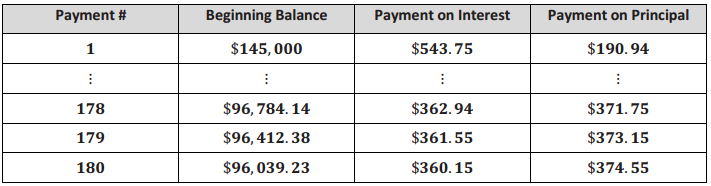
d. In Julia’s neighborhood, her home has grown in value at around 2.95% per year. Considering how much she still owes the bank, how much of her home does she own after 15 years (the equity in her home)? Express your answer in dollars to the nearest thousand and as a percent of the value of her home.
Answer:
Julia’s home is worth 145000(1.0295)15 ≈ 224265.91, which is about $224, 000. She owes $96,039.23, which still leaves $224,000 – $96,000 = $128,000. This means she owns about $128,000 of her home or \(\frac{128}{224}\) = \(\frac{4}{7}\) ≈ 57% of her home.
e. Reasoning from your graph in part (b) and the table above, If both you and Julia sell your homes in 15 years at the homes’ appreciated values, who would have more equity?
Answer:
Answers will vary. Any student whose home is worth more than $83,000 initially will have more equity than Julia after 15 years, which should be clear from the graph.
f. How much more do you need to save over 15 years to have assets over $1,000,000?
Answer:
Answers will vary. For example:
$1,000,000 – $294,000 = $706,000
I will need to save $706,000 in the next 15 years.
Eureka Math Algebra 2 Module 3 Lesson 33 Mathematical Modeling Exercise Answer Key
Mathematical Modeling Exercises:
Assume you can earn 7% interest annually, compounded monthly, in an investment account. Develop a savings plan so that you will have $1 million in assets in 15 years (including the equity in your paid-off house).
Exercise 1.
Use your answer to Opening Exercise, part (g) as the future value of your savings plan.
a. How much will you have to save every month to save up $1 million in assets?
Answer:
Answers will vary. For example, since i = \(\frac{0.07}{12}\) ≈ 0.00583, Af = 706000, and n = 180,
706000 = R\(\left(\frac{(1+0.00583)^{180}-1}{0.00583}\right)\)
R = 706000 . \(\frac{0.00583}{(1.00583)^{180}-1}\)
R ≈ 2228.17
The monthly payment to save $706,000 in 15 years at 7% interest compounded quarterly would be $2,228.17.
b. Recall the monthly payment to pay off your home in 15 years (from Problem 1 of the Problem Set of Lesson 32). How much are the two together? What percentage of your monthly Income is this for the profession you chose?
Answer:
The monthly payment on a 15-year loan was about $1,352 (a 5% annual interest loan on $171,000 for a $190,000 house with $19,000 down for 15 years). The savings payment coupled with the monthly mortgage comes to about $3,579. Answers will vary on the percentage of monthly income.
Exercise 2.
Write a report supported by the calculations you did above on how to save $1 million (or more) in your lifetime.
Answer:
Answers will vary.
You may wish to assign this as homework so students can type up their plan, make a slide presentation, blog about it, write it in their journal, etc.
Eureka Math Algebra 2 Module 3 Lesson 33 Problem Set Answer Key
Question 1.
Consider the following scenario: You would like to save up $50, 000 after 10 years and plan to set up structured savings plan to make monthly payments at 4. 125% interest annually, compounded monthly.
a. What lump sum amount would you need to invest at this interest rate in order to have $50, 000 after 10 years?
Answer:
50000 = P\(\left(1+\frac{0.04125}{12}\right)^{120}\)
P = 50000 ÷ \(\left(1+\frac{0.04125}{12}\right)^{120}\)
P ≈ 33123.08
You would need to deposit $33,123.08 now to save up to $50,000.
b. Use an online amortization calculator to find the monthly payment necessary to take a loan for the amount in part (a) at this interest rate and for this time period.
Answer:
$337.33
c. Use Af = R\(\left(\frac{(1+i)^{n}-1}{i}\right)\) to solve for R.
Answer:
50000 = R\(\left(\frac{\left(1+\frac{0.04125}{12}\right)^{120}-1}{\frac{0.04125}{12}}\right)\)
R ≈ 337.33
The monthly payment would be $337.33.
d. Compare your answers to part (b) and part (c). What do you notice? Why did this happen?
Answer:
The answers are the same. The present value of an annuity is the cost of a loan and can be found by setting the loan equal to the compound interest formula, which is what we did originally. Once we had the cost of a loan, the amortization calculator was able to find the monthly payment. In port (c) we used the future value of an annuity to find the same quantity.
Question 2.
For structured savings plans, the future value of the savings plan as a function of the number of payments made at that point is an interesting function to examine. Consider a structured savings plan with a recurring payment of $450 made monthly and an annual interest rate of 5.875% compounded monthly.
a. State the formula for the future value of this structured savings plan as a function of the number of payments made. Use f for the function name.
Answer:
f(x) = 450\(\left(\frac{\left(1+\frac{0.05875}{12}\right)^{x}-1}{\left(\frac{0.05875}{12}\right)}\right)\)
b. Graph the function you wrote in part (a) for 0 ≤ x ≤ 216.
Answer:
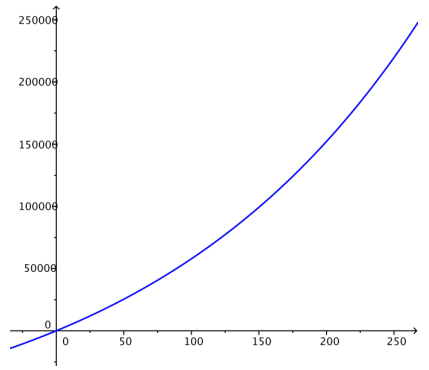
c. State any trends that you notice for this function.
Answer:
The function appears to be exponential in nature, it is increasing at an increasing rate.
d. What is the approximate value of the function f for x = 216?
Answer:
f(216) =450 \(\left(\frac{\left(1+\frac{0.05875}{12}\right)^{216}-1}{\left(\frac{0.05875}{12}\right)}\right)\)
≈ 172041.21
e. What is the domain of f? Explain.
Answer:
Since the compounding is monthly, the domain off is normally considered to be a positive integer (i.e., the number of periods).
f. If the domain of the function is restricted to natural numbers, is the function a geometric sequence? Why or why not?
Answer:
No, the function is not a geometric sequence, since it does not have a common ratio. For instance, from x = 1 to x = 2, the value of the ratio is approximately 2.004896, but from x = 2 to x = 3, the value of the ratio is 1.50367.
g. Recall that the nth partial sums of a geometric sequence can be represented with Sn It is true that f(x) = Sx for positive integers x, since it is a geometric sequence; that is, Sx = \(\sum_{i=1}^{x} a r^{i}\). State the geometric sequence whose sums of the first x terms are represented by this function.
Answer:
The geometric sequence has first term 450 and common ratio (1 + \(\frac{0.05875}{12}\)). It can be written as
an = \(\left(1+\frac{0.05875}{12}\right)^{n-1}\)
h. April has been following this structured savings plan for 18 years. April says that taking out the money and starting over should not affect the total money earned because the interest rate does not change. Explain why April is incorrect in her reasoning.
Answer:
The function is increasing exponentially, so the larger the balance, the more it grows. If the money is taken out, then the growth would be reset back to the beginning, although you would have that money.
Question 3.
Henry plans to have $195,000 in property in 14 years and would like to save up to $1 million by depositing $3,068.95 each month at 6% interest per year, compounded monthly. Tina’s structured savings plan over the same time span is described in the following table:
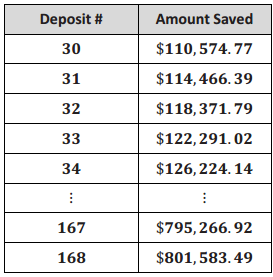
a. Who has the higher interest rate? Who pays more every month?
Answer:
From the table it looks like Tina pays more every month but Henry has the higher interest rate. Henry would have about $99, 000 after 30 payments, but Tina has more at that point. After 168 payments, Henry will save up $805,000, while Tina has only saved $801, 583. Over long periods of time, a higher interest rate will eventually beat larger payments.
b. At the end of 14 years, who has more money from their structured savings plan? Does this agree with what you expected? Why or why not?
Answer:
Henry has more, but just barely. The larger payment Tina was making was not enough to stay ahead of Henry for 14 years, but he looks to have just passed her recently.
c. At the end of 40 years, who has more money from their structured savings plan?
Answer:
Henry has extended his lead significantly by this point. Once he overtakes Tina, his savings continues to grow at a faster rate than Tina’s savings.
Question 4.
Edgar and Paul are two brothers that each get an inheritance of $150,000. Both plan to save up over $1,000,000 in 25 years. Edgar takes his inheritance and deposits the money into an investment account earning 8% interest annually, compounded monthly, payable at the end of 25 years. Paul spends his inheritance but uses a structured savings plan that is represented by the sequence bn = 1275 + bn – 1 . (1 + \(\frac{0.0775}{12}\)) with b0 = 1275 in order to save up more than $1,000,000.
a. Which of the two has more money at the end of 25 years?
Answer:
Let E(x) represent Edgar’s savings and P(x) represent Paul’s savings.
Then E(x) = 150000(1 + \(\frac{0.08}{12}\))300 ≈ 1101026.40.
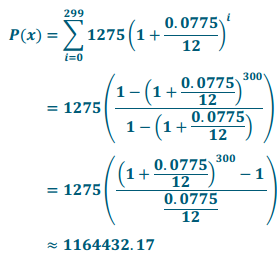
Paul has $63,405.78 more than Edgar at the end of 25 years.
b. What are the pros and cons of both brothers’ plans? Which would you rather do? Why?
Answer:
Answers will vary between the two plans and may include a combination of both.
Edgar only has to make a single payment, and he inherited the money, so it does not come out of his normal budget. He does not have to worry about the account again, but he makes less money than Paul overall and cannot access the money until the end of the 25 years. Edgar also pays much less than Paul does.
Paul ends up paying $382,500 in order to save up his million, but he does this slowly over the 25 years, so he does not have a huge pinch at any point in time. Paul ends up saving more money in the long run.
Eureka Math Algebra 2 Module 3 Lesson 33 Exit Ticket Answer Key
Question 1.
At age 25, you begin planning for retirement at 65. Knowing that you have 40 years to save up for retirement and expecting an Interest rate of 4% per year, compounded monthly, throughout the 40 years, how much do you need to deposit every month to save up $2 million for retirement?
Answer:
Af = R\(\left(\frac{(1+i)^{n}-1}{i}\right)\)
2 × 106 = R\(\left(\frac{\left(1+\frac{0.04}{12}\right)^{12 \cdot 40}-1}{\frac{0.04}{12}}\right)\)
R = 2 2 × 106 . \(\left(\frac{0.04}{12}\right) \div\left(\left(1+\frac{0.04}{12}\right)^{480}-1\right)\)
R ≈ 1692.10
You need to deposit $1,692.10 every month for 40 years to save $2 million at 4% interest.
Question 2.
Currently, your savings for each month is capped at $400. If you start investing all of this into a savings plan earning 1% interest annually, compounded monthly, then how long should it take to save $160,000? (Hint: Use logarithms.)
Answer:
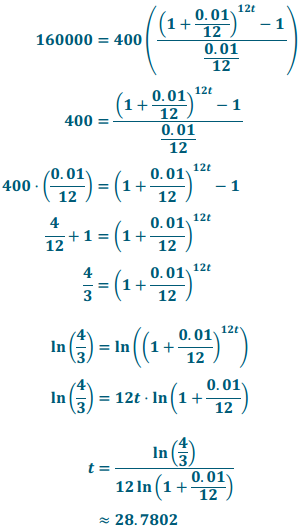
It would take 28 years and 10 months to save up $160,000 with only $400 deposited every month.