Engage NY Eureka Math Algebra 2 Module 2 Lesson 9 Answer Key
Eureka Math Algebra 2 Module 2 Lesson 9 Example Answer Key
Example 1.
Convert from degrees to radians: 45°
Answer:
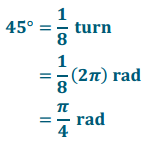
Example 2.
Convert from degrees to radians: 33°
Answer:
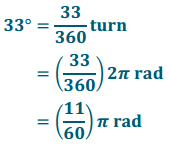
Example 3.
Convert from radians to degrees: –\(\frac{\pi}{3}\) rad
Answer:
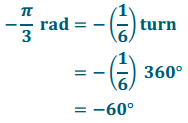
Example 4.
Convert from radians to degrees: \(\frac{19 \pi}{17}\) rad
Answer:
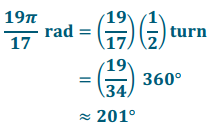
Eureka Math Algebra 2 Module 2 Lesson 9 Opening Exercise Answer Key
Let’s construct the graph of the function y = sin(x°), where x is the measure of degrees of rotation. In Lesson 5, we decided that the domain of the sine function is all real numbers and the range is [- 1, 1]. Use your calculator to complete the table below with values rounded to one decimal place, and then graph the function on the axes below. Be sure that your calculator is in degree mode.
| X, in degrees | y = sin(x°) |
| 0 | |
| 30 | |
| 45 | |
| 60 | |
| 90 | |
| 120 |
Answer:
| X, in degrees | y = sin(x°) |
| 0 | 0.0 |
| 30 | 0.5 |
| 45 | 0.7 |
| 60 | 0.9 |
| 90 | 1.0 |
| 120 | 0.9 |
| X, in degrees | y = sin(x°) |
| 135 | |
| 150 | |
| 180 | |
| 210 | |
| 225 | |
| 240 |
Answer:
| X, in degrees | y = sin(x°) |
| 135 | 0.7 |
| 150 | 0.5 |
| 180 | 0.0 |
| 210 | -0.5 |
| 225 | -0.7 |
| 240 | -0.9 |
| X, in degrees | y = sin(x°) |
| 270 | |
| 300 | |
| 315 | |
| 330 | |
| 360 |
Answer:
| X, in degrees | y = sin(x°) |
| 270 | -1.0 |
| 300 | -0.9 |
| 315 | -0.7 |
| 330 | -0.5 |
| 360 | 0.0 |
Eureka Math Algebra 2 Module 2 Lesson 9 Exercise Answer Key
Set your calculator’s viewing window to 0 ≤ x ≤ 10 and – 2.4 ≤ y ≤ 2.4, and be sure that your calculator is in degree mode. Plot the following functions in the same window:
y = sin(x°)
y = sin(2x°)
y = sin(10x°)
y = sin(50x°)
y = sin(100x°)
Exercise 1.
This viewing window was chosen because it has close to the same scale in the horizontal and vertical directions. In this viewing window, which of the five transformed sine functions most clearly shows the behavior of the sine function?
Answer:
Students may answer y = sin(50x°) or y = sin(100x°). (Either answer is reasonable.)
Exercise 2.
Describe the relationship between the steepness of the graph y = sin(kx°) near the origin and the value of k.
Answer:
As we increase k, the steepness of the graph y = sin(kx°) near the origin increases.
Exercise 3.
Since we can control the steepness of the graph y = sin(kx°) near the origin by changing the value of k, how steep might we want this graph to be? What is your favorite positive slope for a line through the origin?
Answer:
It would make sense to try to get the steepness at the origin to be the same as the diagonal line y = x, which has slope 1.
Exercise 4.
In the same viewing window on your calculator, plot y = x and y = sin(kx°) for some value of k. Experiment with your calculator to find a value of k so that the steepness of y = sin(kx°) matches the slope of the line y = x near
the origin. You may need to change your viewing window to 0 ≤ x ≤ 2 and 0 ≤ y ≤ 1 to determine the best value of k.
Answer:
The graph of y = sin(57x°) has nearly the same steepness as the diagonal line with equation y = x.
Exercise 5.
Use a protractor that measures angles in degrees to find an approximate degree measure for an angle with measure 1 rad. Use one of the figures from the previous discussion.
Answer:
We find that the degree measure of an angle that has measure 1 rad is approximately 57°.
Exercise 6.
Complete the table below, converting from degrees to radians or from radians to degrees as necessary. Leave your answers in exact form, involving π.
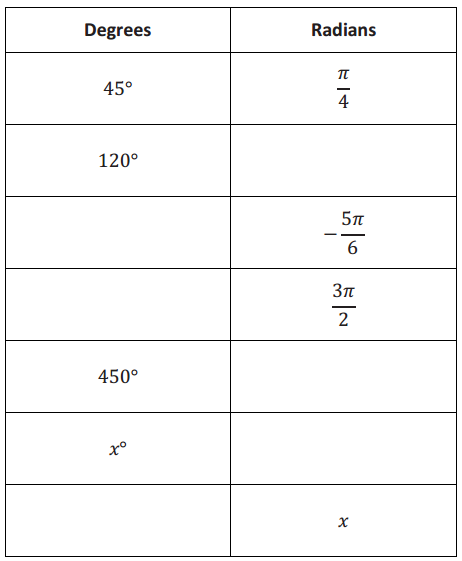
Answer:
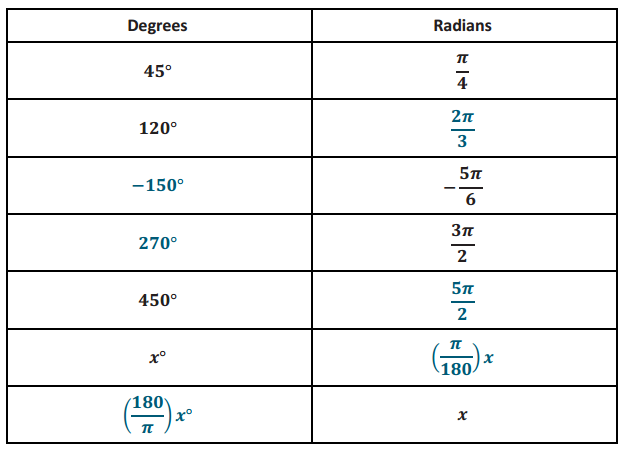
Exercise 7.
On your calculator, graph the functions y = x and y = sin\(\left(\frac{180}{\pi} x^{\circ}\right)\) What do you notice near the origin? What is the decimal approximation to the constant \(\frac{180}{\pi}\) to one decimal place? Explain how this relates to what we’ve done in Exercise 4.
Answer:
The graph of y = sin \(\left(\frac{180}{\pi} x^{\circ}\right)\) is nearly identical to the graph of y = x near the origin. On the calculator, we see that \(\frac{180}{\pi}\) ≈ 57.3 so that sin \(\left(\frac{180}{\pi} x^{\circ}\right)\) ≈ sin(57x°). This is the function we were looking for in Exercise 4.
Eureka Math Algebra 2 Module 2 Lesson 9 Problem Set Answer Key
Question 1.
Use a radian protractor to measure the amount of rotation In radians of ray BA to ray BC in the indicated direction. Measure to the nearest 0. 1 radian. Use negative measures to indicate clockwise rotation.
a.
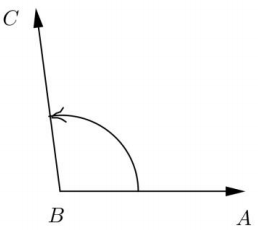
Answer:
1.7 rad
b.
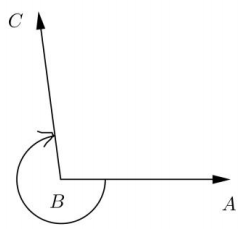
Answer:
– 4.6 rad
c.
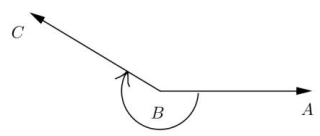
Answer:
– 3.4 rad
d.
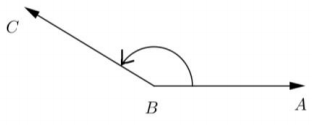
Answer:
2.6 rad
e.
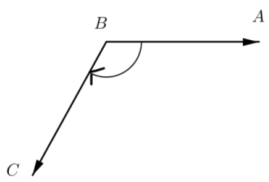
Answer:
– 2.1 rad
f.
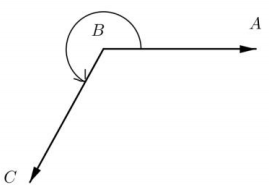
Answer:
4.2 rad
g.
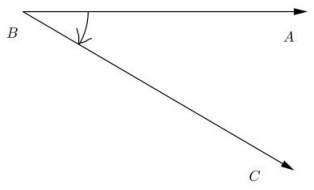
Answer:
– 0.4 rad
h.
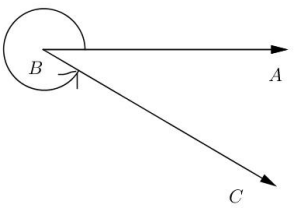
Answer:
5.8 rad
Question 2.
Complete the table below, converting from degrees to radians. Where appropriate, give your answers in the form of a fraction of π.
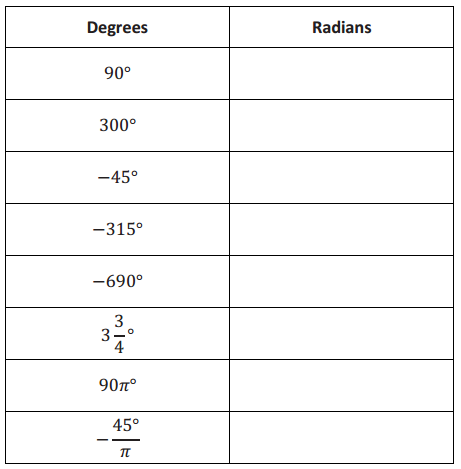
Answer:
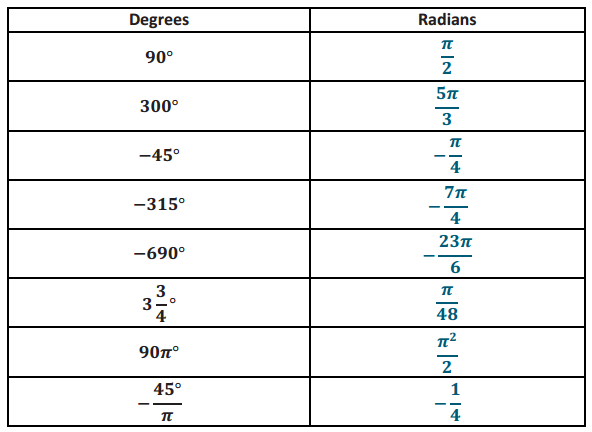
Question 3.
Complete the table below, converting from radians to degrees.
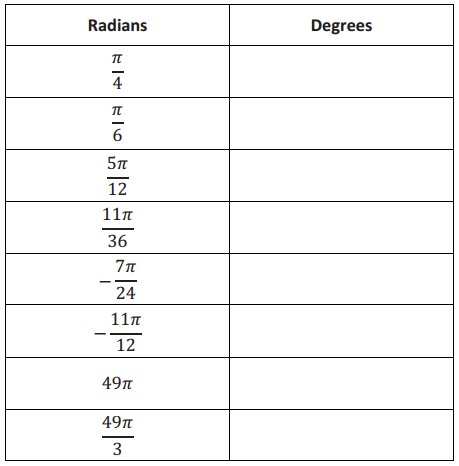
Answer:
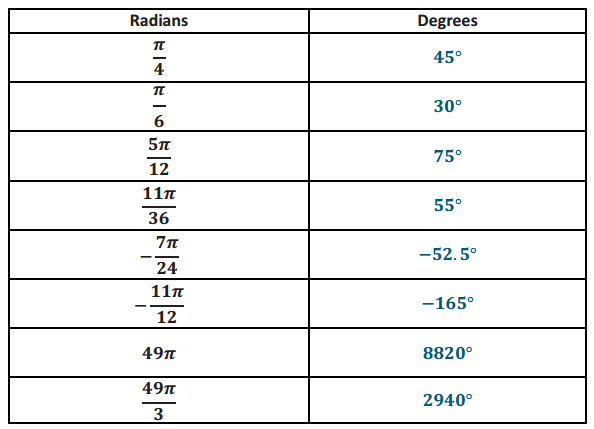
Question 4.
Use the unit circle diagram from the end of the lesson and your knowledge of the six trigonometric functions to complete the table below. Give your answers in exact form, as either rational numbers or radical expressions.
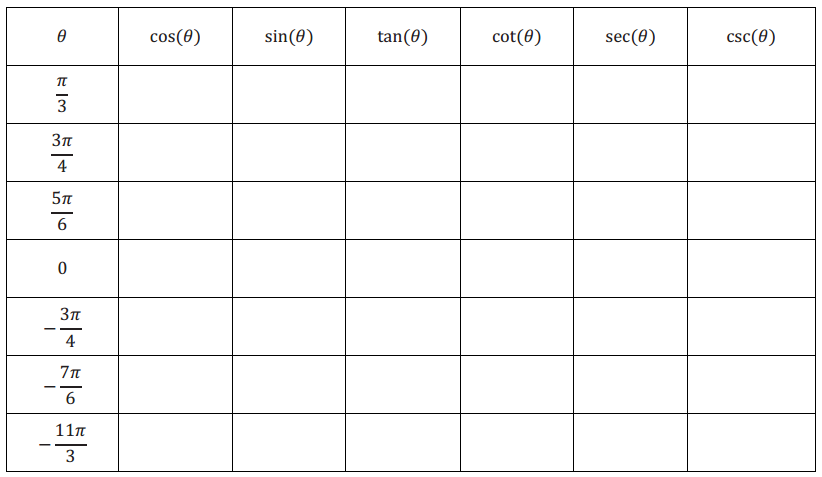
Answer:
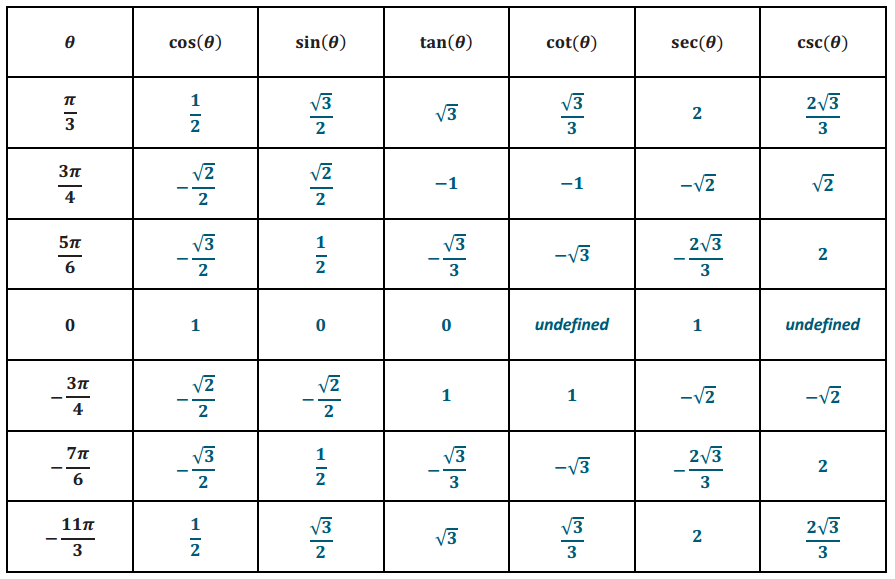
Question 5.
Use the unit circle diagram from the end of the lesson and your knowledge of the sine, cosine, and tangent functions to complete the table below. Select values of θ so that 0 ≤ θ ≤ 2π.
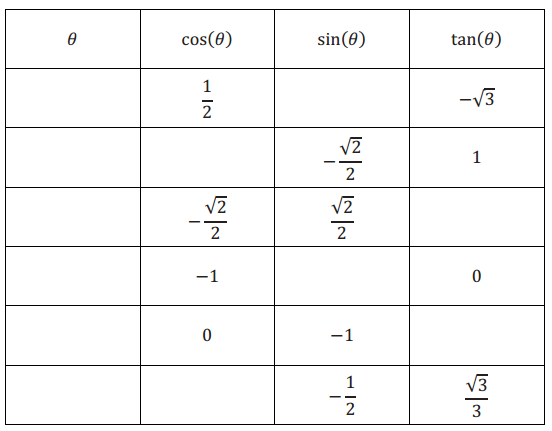
Answer:
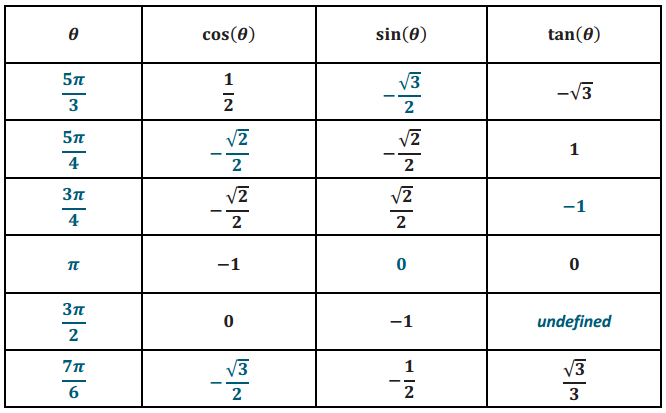
Question 6.
How many radians does the minute hand of a clock rotate through over 10 minutes? How many degrees?
Answer:
In 10 minutes, the minute hand makes \(\frac{1}{6}\) of a rotation, so it rotates through \(\frac{1}{6}\)(2π) = \(\frac{\pi}{3}\)radians. This is equivalent to 60°.
Question 7.
How many radians does the minute hand of a clock rotate through over half an hour? How many degrees?
Answer:
In 30 minutes, the minute hand makes \(\frac{1}{2}\) of a rotation, so it rotates through \(\frac{1}{2}\)(2π) = π radians. This is equivalent to 180°.
Question 8.
What is the radian measure of an angle subtended by an arc of a circle with radius 4 cm if the intercepted arc has length 14 cm? How many degrees?
Answer:
The intercepted arc is the length of 3.5 radii, so the angle subtended by that arc measures 3.5 radians. This is equivalent to 3.5 \(\left(\frac{180^{\circ}}{\pi}\right)\) = \(\frac{630^{\circ}}{\pi}\) ≈ 200.5 .
Question 9.
What is the radian measure of an angle formed by the minute and hour hands of a clock when the clock reads 1:30? How many degrees? (Hint: You must take into account that the hour hand is not directly on the 1.)
Answer:
At 1:30, the hour hand is halfway between the 1 and the 2, and the minute hand is on the 6. A hand on the clock rotates through \(\frac{1}{12}\) of a rotation as it moves from one number to the next. Since there are 4\(\frac{1}{2}\) of these increments between the two hands of the clock at 1:30, the angle formed by the two clock hands is \(\frac{9}{2}\left(\frac{1}{12}\right)\)(2π) = \(\frac{3 \pi}{4}\)radians. In degrees, this is 135°.
Question 10.
What is the radian measure of an angle formed by the minute and hour hands of a clock when the clock reads 5:45? How many degrees?
Answer:
At 5:45, the hour hand is \(\frac{3}{4}\) of the way between the 5 and 6 on the clock face, and the minute hand is on the 9. Then there are 3\(\frac{1}{4}\) increments of \(\frac{1}{12}\) of a rotation between the two hands of the clock at 5:45, so the angle formed by the two clock hands is \(\left(\frac{13}{4}\right)\left(\frac{1}{12}\right)\) (2π) = \(\frac{13}{24}\)π radians. This is equivalent to \(\frac{13 \pi}{24}\left(\frac{180^{\circ}}{\pi}\right)\) = 97.50°.
Question 11.
How many degrees does the earth revolve on its axis each hour? How many radians?
Answer:
The earth revolves through 360° in 24 hours, so it revolves \(\frac{360^{\circ}}{24}\) = 15° each hour.
Question 12.
The distance from the equator to the North Pole is almost exactly 10,000 km.
a. Roughly how many kilometers is 1 degree of latitude?
Answer:
There are 90 degrees of latitude between the equator and the North Pole, so each degree of latitude is \(\frac{1}{90}\) (1oooo) ≈ 111.1km.
b. Roughly how many kilometers is 1 radian of latitude?
Answer:
There are \(\frac{\pi}{2}\) radians of latitude between the equator and the North Pole, so each radian of latitude is \(\frac{2}{\pi}\)(1o,ooo) ≈ 6,366.2km.
Eureka Math Algebra 2 Module 2 Lesson 9 Exit Ticket Answer Key
Question 1.
Convert 60° to radians.
Answer:
60° = \(\frac{\pi}{3}\) rad
Question 2.
Convert –\(\frac{\pi}{2}\) rad to degrees.
Answer:
–\(\frac{\pi}{2}\) rad = – 90°
Question 3.
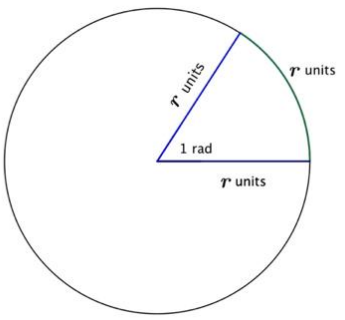
Explain how radian measure is related to the radius of a circle. Draw and label an appropriate diagram to support your response.
Answer:
If we take one radius from the circle and wrap it part of the way around the circle, the central angle with the arc length of one radius has measure one radian.