Engage NY Eureka Math Algebra 2 Module 2 Lesson 6 Answer Key
Eureka Math Algebra 2 Module 2 Lesson 6 Example Answer Key
Example 1.
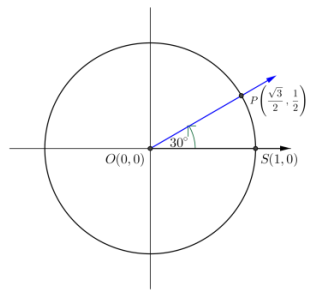
Suppose that point P is the point on the unit circle obtained by rotating the initial ray through 30°. Find tan(30°).
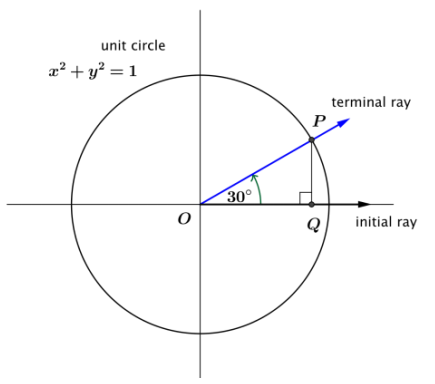
Answer:
→ What is the length QQ of the horizontal leg of ∆ OPQ?
By remembering the special triangles from Geometry, we have OQ = \(\frac{\sqrt{3}}{2}\).
→ What is the length QP of the vertical leg of ∆ OPQ?
Either by the Pythagorean theorem, or by remembering the special triangles from Geometry, we have QP = \(\frac{1}{2}\).
→ What are the coordinates of point P?
\(\left(\frac{\sqrt{3}}{2}, \frac{1}{2}\right)\)
→ What are cos(30°) and sin(30°)?
cos(30°) = \(\frac{\sqrt{3}}{2}\), and sin(30°) = \(\frac{1}{2}\).
→ What is tan(30°)?
tan(30°) = \(\frac{1}{\sqrt{3}}\) With no radicals in the denominator, this is tan(30°) = \(\frac{\sqrt{3}}{3}\).
Eureka Math Algebra 2 Module 2 Lesson 6 Opening Exercise Answer Key
Let P(xθ, yθ) be the point where the terminal ray intersects the unit circle after rotation by θ degrees, as shown in the diagram below.
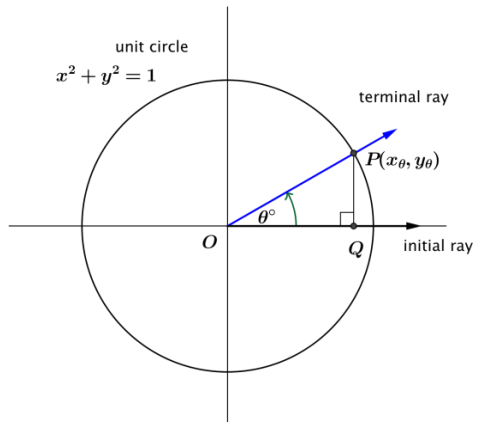
a. Using triangle trigonometry, what are the values of xθ and yθ in terms of θ?
Answer:
xθ = cos(θ°), and yθ = sin(θ°)
b. Using triangle trigonometry, what is the value of tan(θ°) in terms of xθ and yθ?
Answer:
tan(θ°) = \(\frac{y_{\theta}}{x_{\theta}}\)
c. What is the value of tan(θ°) in terms of θ?
Answer:
tan(θ°) = \(\frac{\sin \left(\theta^{\circ}\right)}{\cos \left(\theta^{\circ}\right)}\)
Eureka Math Algebra 2 Module 2 Lesson 6 Exercise Answer Key
Exercise 1.
For each value of θ in the table below, use the given values of sin(θ°) and cos(θ°) to approximate tan(θ°) to two decimal places.
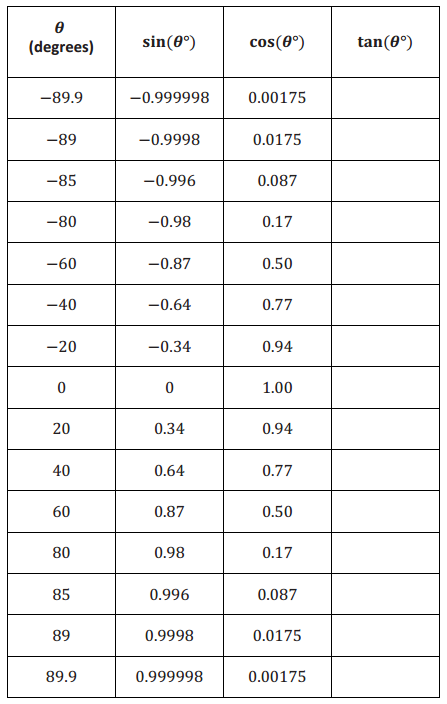
Answer:
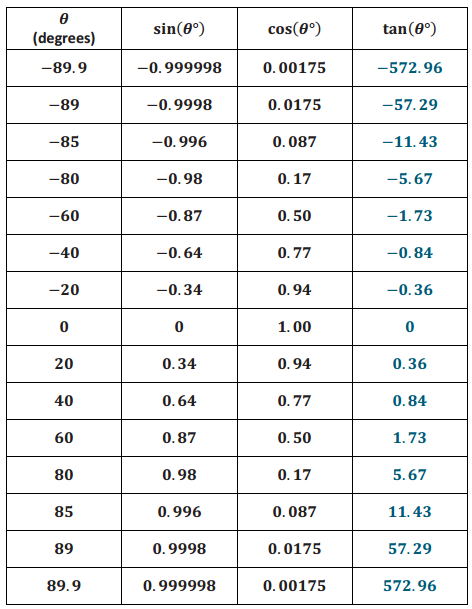
a. As θ → -90° and θ > -90°, what value does sin(θ°) approach?
Answer:
– 1
b. As θ →‚ -90° and θ > -90°, what value does cos(θ°) approach?
Answer:
0
c. As θ →‚ -90° and θ > -90°, how would you describe the value of tan(θ°) = \(\frac{\sin \left(\theta^{\circ}\right)}{\cos \left(\theta^{\circ}\right)}\)
Answer:
tan(θ°) → -∞
d. As θ → 90° and θ < 90°, what value does sin(θ°) approach?
Answer:
1
e. As θ → 90° and θ < 90°, what value does cos(θ°) approach?
Answer:
0
f. As θ → 90° and θ < 90°, how would you describe the behavior of tan(θ°) = \(\frac{\sin \left(\theta^{\circ}\right)}{\cos \left(\theta^{\circ}\right)}\)
Answer:
tan(θ°) → ∞
g. How can we describe the range of the tangent function?
Answer:
The range of the tangent function is (- ∞, ∞), which is the set of all real numbers.
Exercise 2.
Let P be the point on the unit circle with center O that is the intersection of the terminal ray after rotation by θ degrees as shown in the diagram. Let Q be the foot of the perpendicular line from P to the x-axis, and let the line l be the line perpendicular to the x-axis at S(1, 0). Let R be the point where the secant line OP intersects the line f. Let m be the length of \(\overline{\boldsymbol{R} S}\).
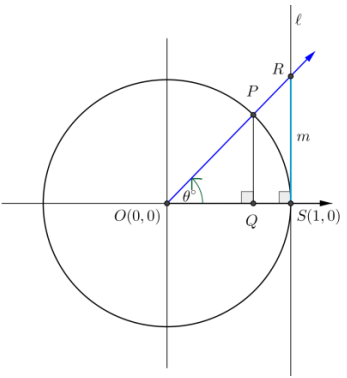
a. Show that m = tan(θ°).
Answer:
Segment RS has length m, and side \(\overline{O S}\) adjacent to ∠ROS has length 1, so we use tangent:
tan(θ°) = \(\frac{m}{1}\) = m
Thus, m = tan(θ°).
b. Using a segment in the figure, make a conjecture why mathematicians named the function f(θ°) = \(\frac{\sin \left(\theta^{\circ}\right)}{\cos \left(\theta^{\circ}\right)}\) the tangent function.
Answer:
Mathematicians named the function tangent because the value of the function is the length of the segment RS that is tangent to the circle.
c. Why can you use either triangle, ∆ POQ or ∆ ROS, to calculate the length m? Answer:
These triangles are similar by AA similarity (both are right triangles that share a common acute angle); hence, their sides are proportional.
d. Imagine that you are the mathematician who gets to name the function. (How cool would that be?) Based upon what you know about the equations of lines, what might you have named the function instead?
Answer:
I would have called it the slope function instead because the slope of the secant line OR is also m.
Exercise 3.
Draw four pictures similar to the diagram in Exercise 2 to illustrate what happens to the value of tan(θ°) as the rotation of the secant line through the terminal ray increases towards 90°. How does your diagram relate to the work done in Exercise 1?
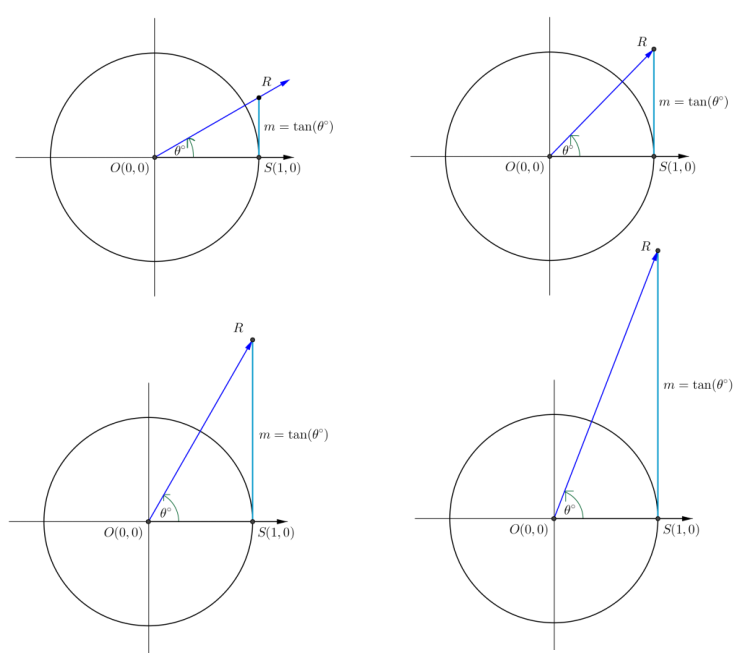
Answer:
As the rotation increases to 90 degrees, the value of m increases to positive infinity. Since m = tan(θ°), the value of tan (θ°) also increases to positive infinity. This is what was observed numerically in Exercise 1.
Exercise 4.
When the terminal ray is vertical, what is the relationship between the secant line OR and the tangent line RS? Explain why you cannot determine the measure of m in this instance. What is the value of tan(90°)?
Answer:
The secant line and tangent line are parallel when the terminal ray is vertical. The value of m cannot be determined because parallel lines do not intersect. Therefore, no triangle is formed, and triangle trigonometry does not apply. The tangent function is undefined at θ = 90.
Exercise 5.
When the terminal ray is horizontal, what Is the relationship between the secant line OR and the x-axis? Explain what happens to the value of m in this instance. What is the value of tan(0°)?
Answer:
When the secant line OR is horizontal, then it coincides with the x-axis. The value of m is zero since the points R and S are the same. Then, m = 0, and thus tan(0°) = 0.
Exercise 6.
When the terminal ray is rotated counterclockwise about the origin by 45°, what is the relationship between the value of m and the length of \(\overline{O S}\)? What Is the value of tan(45°)?
Answer:
In this case, m = OS. Since \(\overline{O S}\) is a radius of the unit circle, m = 1. Thus, tan(45°) = 1.
Exercise 7.
Rotate the initial ray about the origin the stated number of degrees. Draw a sketch and label the coordinates of point P where the terminal ray intersects the unit circle. What is the slope of the line containing this ray?
a. 30°
Answer:
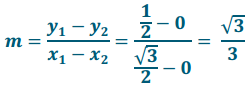
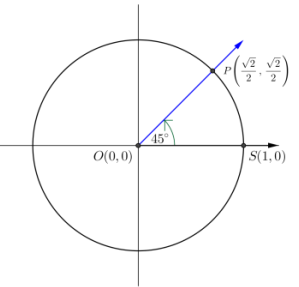
b. 45°
Answer:
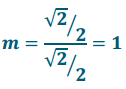
c. 60°
Answer:
m = \(\frac{\sqrt{3} / 2}{1 / 2}\) = \(\sqrt{3}\)
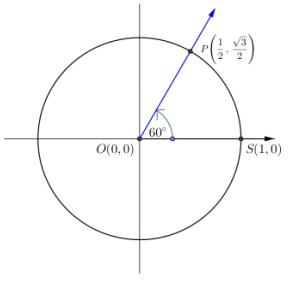
d. Use the definition of tangent to find tan(30°), tan(45°), and tan(60°). How do your answers compare to your work in parts (a) – (c)?
Answer:
The slopes and the values of the tangent functions at each rotation were the same. That is, tan (30°) = \(\frac{\sqrt{3}}{3}\), tan(45°) = 1, and tan(60°) = √3
e. If the initial ray is rotated θ degrees about the origin, show that the slope of the line containing the terminal ray is equal to tan(θ°). Explain your reasoning.
Answer:
The terminal ray will always intersect the unit circle at (xθ, yθ) = (cos(θ°), sin(θ°)) and will always pass through the origin, (0, 0). Thus, the slope of the line containing the terminal ray will always be given by
m = \(\frac{\sin \left(\theta^{\circ}\right)-0}{\cos \left(\theta^{\circ}\right)-0}=\frac{\sin \left(\theta^{\circ}\right)}{\cos \left(\theta^{\circ}\right)}\) = tan (θ°)
f. Now that you have shown that the value of the tangent function is equal to the slope of the terminal ray, would you prefer using the name tangent function or slope function? Why do you think we use tangent instead of slope as the name of the tangent function?
Answer:
Answers may vary for the first question. Possible reasons include familiarity or comfort with one of the concepts. Tangent is probably used instead of slope due to the historical ideas of trigonometry and geometry.
Exercise 8.
Rotate the initial ray about the origin the stated number of degrees. Draw a sketch and label the coordinates of point P where the terminal ray intersects the unit circle. How does your diagram in this exercise relate to the diagram in the corresponding part of Exercise 7? What is tan(θ°) for these values of θ?
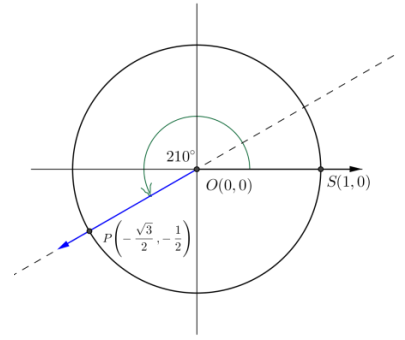
a. 210°
Answer:
From the picture, we can see that the secant is the same line produced by a rotation by 30°, so tan(210°) = tan(30°) = \(\frac{\sqrt{3}}{3}\).
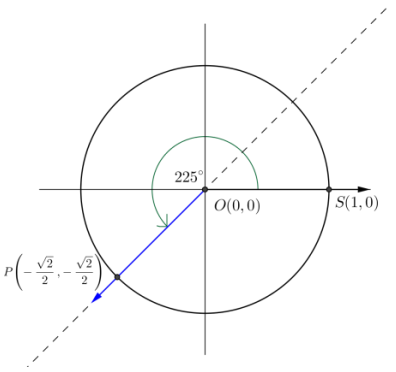
b. 225°
Answer:
From the picture, we can see that the secant is the same line produced by a rotation by 45°, so tan(225°) = tan(45°) = 1.
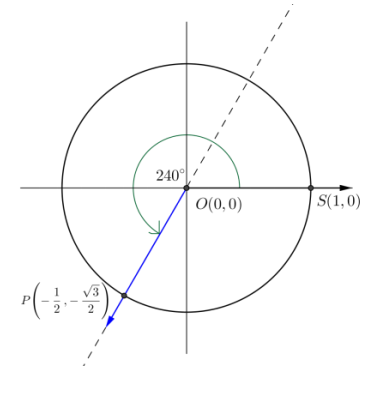
c. 240°
Answer:
From the picture, we can see that the secant is the same line produced by a rotation by 60°, so tan(240°) = tan(60°) = √3.
d. What do the results of parts (a) – (c) suggest about the value of the tangent function after rotating an additional 180 degrees?
Answer:
If the initial ray is rotated by 180 + θ degrees, then the terminal ray is on the same line as the terminal ray when the initial ray is rotated by θ degrees. Since the slope of the line containing the two terminal rays is the same, the value of the tangent function for both θ and 180 + θ is the same.
e. What is the period of the tangent function? Discuss with a classmate and write your conclusions.
Answer:
The period is 180 since rotation by 180 degrees rotates a line to itself.
f. Use the results of Exercise 7(e) to explain why tan(0°) = 0.
Answer:
The slope of any horizontal line is zero.
g. Use the results of Exercise 7(e) to explain why tan(90°) is undefined.
Answer:
The slope of any vertical line is undefined.
Eureka Math Algebra 2 Module 2 Lesson 6 Problem Set Answer Key
Question 1.
Label the missing side lengths, and find the value of tan(θ°) in the following right triangles.
a. θ = 30
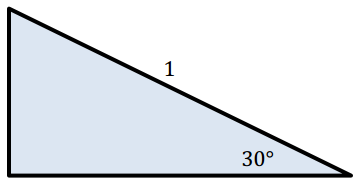
Answer:
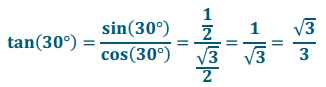
b. θ = 45
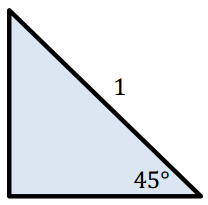
Answer:
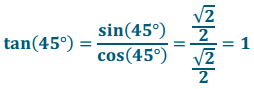
c. θ = 60
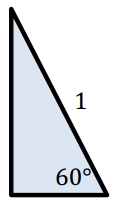
Answer:
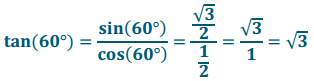
Question 2.
Let θ be any real number. In the Cartesian plane, rotate the initial ray by θ degrees about the origin. Intersect the resulting terminal ray with the unit circle to get point P(xθ, yθ).
a. Complete the table by finding the slope of the line through the origin and the point P.
Answer:
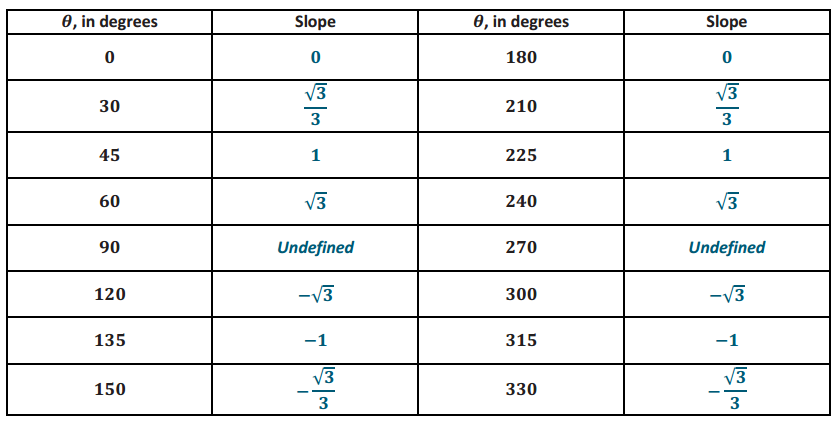
b. Explain how these slopes are related to the tangent function.
Answer:
The slope of the line through the origin and P(xθ, yθ) is equal to tan(θ°).
Question 3.
Consider the following diagram of a circle of radius r centered at the origin. The line l’ is tangent to the circle at S(r, 0), so l is perpendicular to the x-axis.
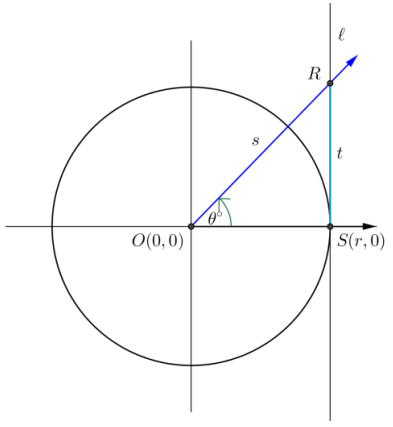
a. If r = 1, then state the value of t in terms of one of the trigonometric functions.
Answer:
t = tan(θ°)
b. If r is any positive value, then state the value of t in terms of one of the trigonometric functions.
Answer:
t = r tan(θ°)
For the given values of r and 8, find t.
c. θ = 30, r = 2
Answer:
t = 2 ∙ tan(30°) = \(\frac{2 \sqrt{3}}{3}\)
d. θ = 45, r = 2
Answer:
t = 2 ∙ tan(45°) = 2 ∙ 1 = 2
e. θ = 45, r = 2
Answer:
t = 2 ∙ tan(60°) = 2 ∙ √3 = 2√3
f. θ = 45, r = 4
Answer:
t = 4 ∙ tan(45°) = 4 ∙ 1 = 4
g. θ = 30, r = 3.5
Answer:
t= 3.5 ∙ tan(30°) = \(\frac{3.5 \sqrt{3}}{3}=\frac{7 \sqrt{3}}{6}\)
h. θ = 0, r = 9
Answer:
t = 9 ∙ tan(θ°) = 9 ∙ 0 = 0
I. θ = 90, r = 5
Answer:
Lines OR and l are distinct parallel lines when θ = 90. Thus, they will never intersect, and the line segment defined by their intersection does not exist.
j. θ = 60, r = √3
Answer:
t = √3 ∙ tan(60°) = √3 ∙ √3 = 3
k. θ = 30, r = 2.1
Answer:
t = 2.1 ∙ tan(30°) = \(\frac{2.1}{\sqrt{3}}=\frac{21}{10 \sqrt{3}}=\frac{7 \sqrt{3}}{10}\)
I. θ = A, r = 3
Answer:
t = 3 ∙ tan(A°) = 3 tan(A°), for A ≠ 90 + 180k,for all integers k.
m. θ = 30, r = b
Answer:
t = b ∙ tan(30°) = \(\frac{b \sqrt{3}}{3}\)
n. Knowing that tan(θ°) = \(\frac{\sin \left(\theta^{\circ}\right)}{\cos \left(\theta^{\circ}\right)}\) for r = 1, find the value of s in terms of one of the trigonometric functions.
Answer:
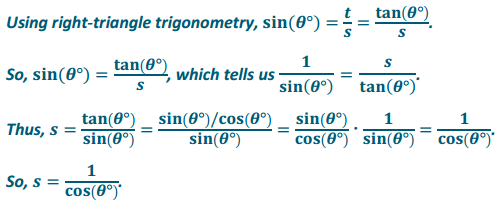
Question 4.
Using what you know of the tangent function, show that – tan(θ°) = tan(-θ°) for θ ≠ 90 + 180k, for all integers
Answer:
The tangent function could also be called the slope function due to the fact that tan (θ°) is the slope of the secant line passing through the origin and intersecting the tangent line perpendicular to the x-axis. If rotation of the secant line by θ° is a counterclockwise rotation, then rotation of the secant line by -θ° is a clockwise rotation. The resulting secant lines will have opposite slopes, so the tangent values will also be opposites. Thus, -tan(θ°) = tan(-θ°).
Eureka Math Algebra 2 Module 2 Lesson 6 Exit Ticket Answer Key
Draw and label a figure on the circle that illustrates the relationship of the trigonometric tangent function tan(θ°) = \(\frac{\sin \left(\theta^{\circ}\right)}{\cos \left(\theta^{\circ}\right)}\) and the geometric tangent line to a circle through the point (1, 0) when θ = 60°. Explain the relationship, labeling the figure as needed.
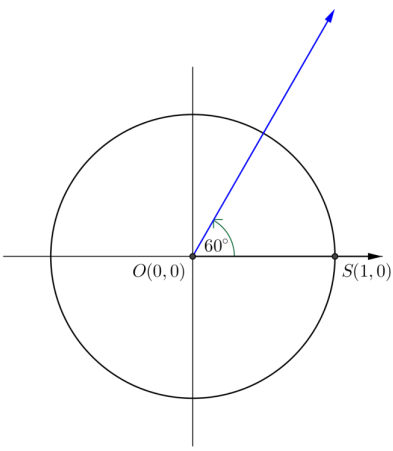
Answer:
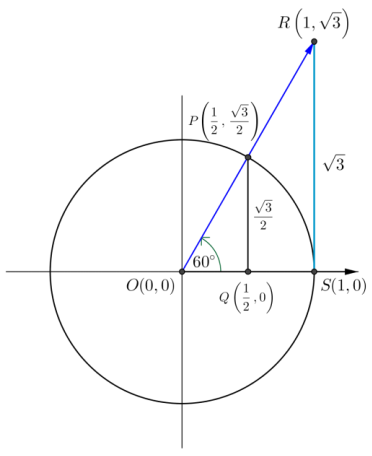
Labeling as shown, lengths are OS = 1, QP = sin(60°) = \(\frac{\sqrt{3}}{2}\), and OQ = cos(60°) = \(\frac{1}{2}\)
Then by similar triangles, we have \(\frac{Q P}{O Q}=\frac{S R}{O S}\) thus, SR = tan(60°) = \(\frac{\sqrt{3} / 2}{1 / 2}=\sqrt{3}\)
Eureka Math Algebra 2 Module 2 Lesson 6 Discussion Answer Key
A description of the tangent function is provided below. Be prepared to answer questions based on your understanding of this function and to discuss your responses with others in your class.
Let θ be any real number. In the Cartesian plane, rotate the nonnegative x-axis by θ degrees about the origin. Intersect the resulting terminal ray with the unit circle to get a point (xθ, yθ). If xθ ≠ 0, then the value of tan(θ°) is \(\frac{y_{\theta}}{x_{\theta}}\). in terms of the sine and cosine functions, tan(θ°) = \(\frac{\sin \left(\theta^{\circ}\right)}{\cos \left(\theta^{\circ}\right)}\) for cos(θ°) ≠ 0.
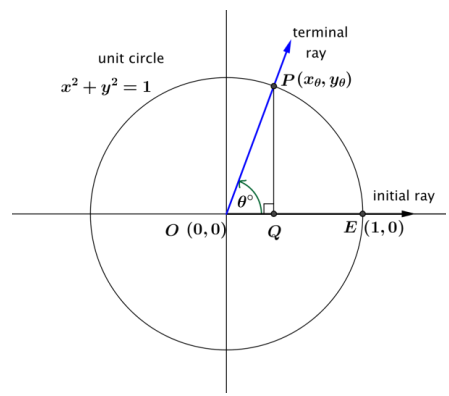
Answer:
→ We have defined the tangent function to be the quotient tan(θ°) = \(\frac{\sin \left(\theta^{\circ}\right)}{\cos \left(\theta^{\circ}\right)}\) for cos(θ°) ≠ 0. Why do we specify that cos(θ°) ≠ 0?
We cannot divide by zero, so the tangent function cannot be defined where the denominator is zero.
→ Looking at the unit circle in the figure, which segment has a measure equal to sin(θ°), and which segment has a measure equal to cos(θ°)?
PQ = sin(θ°), and OQ = cos(θ°).
→ Looking at the unit circle, identify several values of θ that cause tan(θ°) to be undefined. (Scaffolding: When is the x-coordinate of point P zero?)
When cos(θ°) = 0, then tan(θ°) is undefined, which happens when the terminal ray is vertical so that point P lies along the y-axis. The following numbers of degrees of rotation locate the terminal ray along the y-axis: 90, 270, – 90, 450.
→ Describe all numbers θ for which cos(θ°) = 0.
90 + 180k, for any integer k
→ How can we describe the domain of the tangent function, other than all real numbers θ with cos(θ°) ≠ 0?
The domain of the tangent function is all real numbers θ such that θ ≠ 90 + 180k, for all integers k.