Eureka Math Algebra 2 Module 2 Lesson 10 Answer Key

Engage NY Eureka Math Algebra 2 Module 2 Lesson 10 Answer Key

Eureka Math Algebra 2 Module 2 Lesson 10 Problem Set Answer Key

Question 1.
Describe the values of x for which each of the following Is true.
a. The cosine function has a relative maximum.
Answer:
The cosine function has a relative maximum at all x = 2nπ, where n is an integer.

b. The sine function has a relative maximum.
Answer:
The sine function has a relative maximum at all x = \(\frac{\pi}{2}\) + 2πn, where n is an integer.

Question 2.
Without using a calculator, rewrite each of the following in order from least to greatest. Use the graph to explain your reasoning.
sin\(\left(\frac{\pi}{2}\right)\) sin\(\left(-\frac{2 \pi}{3}\right)\) sin\(\left(\frac{\pi}{4}\right)\) sin\(\left(-\frac{\pi}{2}\right)\)

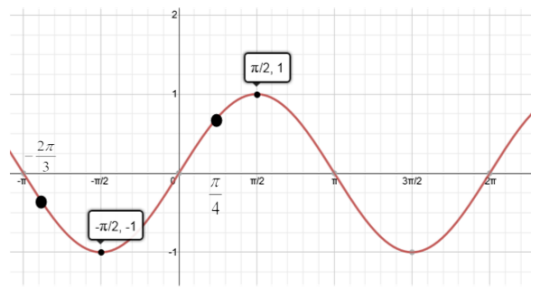
Answer:
At –\(\frac{\pi}{2}\), the sine function takes on its smallest value, and at \(\frac{\pi}{2}\) the sine function takes on its largest value. Additionally, sin\(\) is negative, and sin\(\frac{\pi}{4}\) is positive. Then, these four values in increasing order are
sin\(\left(-\frac{\pi}{2}\right)\), sin\(\left(-\frac{2 \pi}{3}\right)\), sin\(\left(\frac{\pi}{4}\right)\), sin\(\left(\frac{\pi}{2}\right)\).

Question 3.
Without using a calculator, rewrite each of the following in order from least to greatest. Use the graph to explain your reasoning.
cos\(\left(\frac{\pi}{2}\right)\) cos\(\left(\frac{5 \pi}{4}\right)\) cos\(\left(\frac{\pi}{4}\right)\) cos(5π)

Answer:
At 5π, the cosine function takes on its smallest value because 5π = 2π + 2π + π, so cos(5π) = cos(π) = – 1. We can see that cos \(\left(\frac{5 \pi}{4}\right)\) is negative, cos \(\left(\frac{\pi}{2}\right)\) = 0, and cos \(\left(\frac{\pi}{4}\right)\) is positive. Then, these four values in increasing order are
cos(5π), cos \(\left(\frac{5 \pi}{4}\right)\), cos \(\left(\frac{\pi}{2}\right)\), cos \(\left(\frac{\pi}{4}\right)\).

Question 4.
Evaluate each of the following without a calculator using a trigonometric identity when needed.
cos\(\left(\frac{\pi}{6}\right)\)
Answer:
\(\frac{\sqrt{3}}{2}\)

cos\(\left(-\frac{\pi}{6}\right)\)
Answer:
\(\frac{\sqrt{3}}{2}\)

cos\(\left(\frac{7 \pi}{6}\right)\)
Answer:
–\(\frac{\sqrt{3}}{2}\)

cos\(\left(\frac{13 \pi}{6}\right)\)
Answer:
\(\frac{\sqrt{3}}{2}\)

Question 5.
Evaluate each of the following without a calculator using a trigonometric identity when needed.
sin\(\left(\frac{3 \pi}{4}\right)\)
Answer:
\(\frac{\sqrt{2}}{2}\)

sin\(\left(\frac{11 \pi}{4}\right)\)
Answer:
\(\frac{\sqrt{2}}{2}\)

sin\(\left(\frac{7 \pi}{4}\right)\)
Answer:
–\(\frac{\sqrt{2}}{2}\)

sin\(\left(\frac{-5 \pi}{4}\right)\)
Answer:
\(\frac{\sqrt{2}}{2}\)

Question 6.
Use the rotation through θ radians shown to answer each of the following questions.

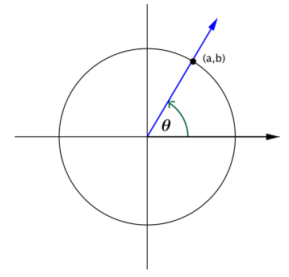
a. Explain why sin(-θ) = -sin(θ) for all real numbers θ.
Answer:
If the initial ray is rotated through -θ radians, It is rotated B radians in the clockwise direction, If the terminal ray of a rotation through θ radians intersects the unit circle at the point (a, b), then the terminal ray of rotation through -θ radians will intersect the unit circle at the point (a, -b). Then, sin(θ) = b and sin(-θ) = -b, so sin(-θ) = -sin(θ).

b. What symmetry does this identity demonstrate about the graph of y = sin(x)?
Answer:
It demonstrates that the graph of y = sin(x) is symmetric with respect to the origin because if the point (x, y) is on the graph, then the point (-x, -y) is also on the graph.

Question 7.
Use the same rotation shown in Problem 6 to answer each of the following questions.
a. Explain why cos(-θ) = cos(θ).
Answer:
If the initial ray is rotated through -θ radians, -t is rotated θ radians in the clockwise direction. If the terminal ray of a rotation through θ radians intersects the unit circle at the point (a, b), then the terminal ray of rotation through -θ radians will intersect the unit circle at the point (a, -b). Then, cos(θ) = a and cos(-θ) = a, so cos(-θ) = cos(θ).

b. What symmetry does this identity demonstrate about the graph of y = cos(θ)?
Answer:
It demonstrates that the graph of y = cos(x) is symmetric with respect to the y-axis because if the point (x, y) is on the graph, then the point (-x, y) is also on the graph.

Question 8.
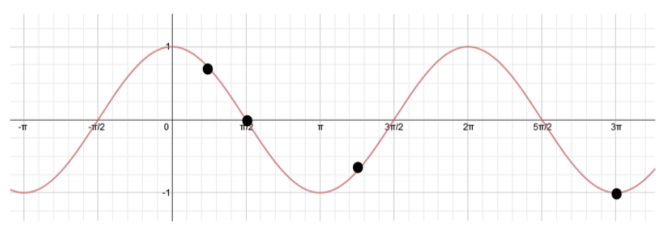
Find equations of two different functions that can be represented by the graph shown below-one sine and one cosine-using different horizontal transformations.

Answer:
y = sin(x – \(\frac{\pi}{2}\)) y = cos(x – π) (other correct answers are possible.)

Question 9.
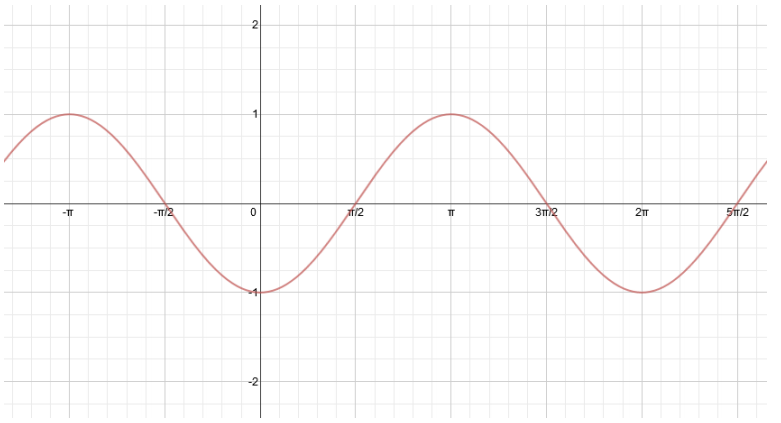
Find equations of two different functions that can be represented by the graph shown below-one sine and one cosine-using different horizontal translations.

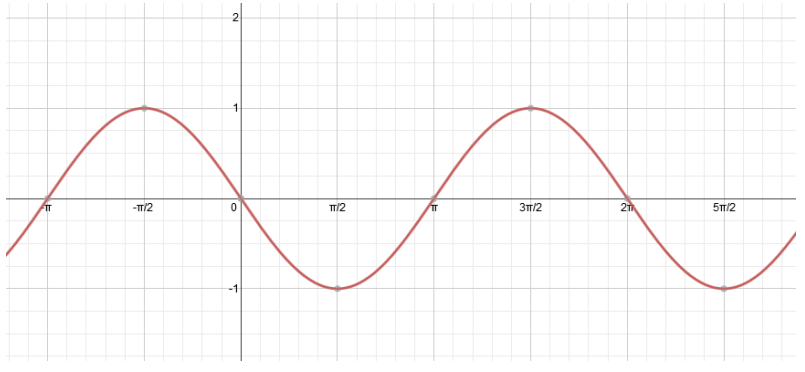
Answer:
y = cos(x + \(\frac{\pi}{2}\)) y = sin(x – π) (other correct answers are possible.)

Eureka Math Algebra 2 Module 2 Lesson 10 Exit Ticket Answer Key

Question 1.
Demonstrate how to evaluate cos \(\left(\frac{8 \pi}{3}\right)\) by using a trigonometric identity.
Answer:
cos\(\left(\frac{8 \pi}{3}\right)\) = cos(\(\frac{2 \pi}{3}\) + 2π) = cos\(\left(\frac{2 \pi}{3}\right)\) = –\(\frac{1}{2}\)

Question 2.
Determine if the following statement is true or false, without using a calculator.
Sin\(\left(\frac{8 \pi}{7}\right)\) = Sin\(\left(\frac{\pi}{7}\right)\)
Answer:
False. sin\(\left(\frac{8 \pi}{7}\right)\) = Sin(\(\frac{\pi}{7}\) + π) = -Sin\(\left(\frac{\pi}{7}\right)\) ≠ Sin\(\left(\frac{\pi}{7}\right)\)

Question 3.
If the graph of the cosine function is translated to the right \(\frac{\pi}{2}\) units, the resulting graph is that of the sine function, which leads to the identity: For all x, sin(x) = cos (x – \(\frac{\pi}{2}\)). Write another identity for sin(x) using a different horizontal shift.
Answer:
sin(x) = cos(x + \(\frac{3\pi}{2}\))

Eureka Math Algebra 2 Module 2 Lesson 10 Exploratory Challenge Answer Key

Exploratory Challenge 1
Consider the function f(x) = sin(x) where x is measured in radians.
Graph f(x) = sin(x) on the interval [-π, 5π] by constructing a table of values. Include all intercepts, relative maximum points, and relative minimum points of the graph. Then, use the graph to answer the questions that follow.


a. Using one of your colored pencils, mark the point on the graph at each of the following pairs of x-values.
x = –\(\frac{\pi}{2}\) and x = –\(\frac{\pi}{2}\) + 2π
x = π and x = π + 2π
x = \(\frac{7 \pi}{4}\) and x = \(\frac{7 \pi}{4}\) + 2π
Answer:

b. What can be said about the y-values for each pair of x-values marked on the graph?
Answer:
For each pair of x-values, the y-values are the same.

c. Will this relationship hold for any two x-values that differ by 2π? Explain how you know.
Answer:
Yes. Since the sine function repeats every 2π units, then the relationship described in part (b) will hold for any two x-values that differ by 2π.

d. Based on these results, make a conjecture by filling in the blank below.
For any real number x, sin(x + 2π) = _______ .
Answer:
sin(x + 2π) = sin(x)

e. Test your conjecture by selecting another x-value from the graph and demonstrating that the equation from part (d) holds for that value of x.
Answer:
sin\(\left(\frac{5 \pi}{2}\right)\) = Sin(\(\frac{\pi}{2}\) + 2π) = sin\(\left(\frac{\pi}{2}\right)\) = 1 (Answers will vary.)

f. How does the conjecture in part (d) support the claim that the sine function is a periodic function?
Answer:
The sine function repeats every 2π units because 2π radians is one full turn. Thus, if we rotate the initial ray through x + 2π radians, the terminal ray is in the same position as if we had rotated by x radians.

g. Use this identity to evaluate sin\(\left(\frac{13 \pi}{6}\right)\)
Answer:
sin\(\left(\frac{13 \pi}{6}\right)\) = sin(\(\frac{\pi}{6}\) + 2π) = sin\(\left(\frac{\pi}{6}\right)\) = \(\frac{1}{2}\)

h. Using one of your colored pencils, mark the point on the graph at each of the following pairs of x-values.
x = –\(\frac{\pi}{4}\) and x = –\(\frac{\pi}{4}\) + π
x = 2π and x = 2π + π
x = \(\frac{5 \pi}{2}\) and x = \(\frac{5 \pi}{2}\) + π
Answer:

i. What can be said about the y-values for each pair of x-values marked on the graph?
Answer:
For each pair of x-values, the y-values have the same magnitude but opposite sign.

j. Will this relationship hold for any two x-values that differ by π? Explain how you know.
Answer:
Yes. Since rotating by an additional π radians produces a point in the opposite quadrant with the same reference angle, the sine of the two numbers will have the same magnitude and opposite sign.

k. Based on these results, make a conjecture by filling in the blank below.
For any real number x, sin(x + π) = _________ .
Answer:
sin(x + π) = -sin(x)

i. Test your conjecture by selecting another x-value from the graph and demonstrating that the equation from part (k) holds for that value of x.
Answer:
sin\(\left(\frac{3 \pi}{2}\right)\) = sin(\(\frac{\pi}{2}\) + π) = -sin\(\left(\frac{\pi}{2}\right)\) = -1

m. Is the following statement true or false? Use the conjecture from (k) to explain your answer.
sin\(\left(\frac{4 \pi}{3}\right)\) = -sin\(\left(\frac{\pi}{3}\right)\)
Answer:
This statement is true: sin\(\left(\frac{4 \pi}{3}\right)\) = sin(\(\frac{\pi}{3}\) + π) = -sin\(\left(\frac{\pi}{3}\right)\).

n. Using one of your colored pencils, mark the point on the graph at each of the following pairs of x-values.
x = –\(\frac{3 \pi}{4}\) and x = \(\frac{3 \pi}{4}\)
x = –\(\frac{\pi}{2}\) and x = \(\frac{\pi}{2}\)
Answer:

o. What can be said about the y-values for each pair of x-values marked on the graph?
Answer:
For each pair of x-values, the y-values have the same magnitude but with the opposite sign.

p. Will this relationship hold for any two x-values with the same magnitude but opposite sign? Explain how you know.
Answer:
Yes. If rotation by x radians produces the point (a, b) on the unit circle, then rotation by -x radians will produce a point (a, -b) on the unit circle.

q. Based on these results, make a conjecture by filling in the blank below.
For any real number x, sin(-x) = _________.
Answer:
sin(-x) = – sin(x)

r. Test your conjecture by selecting another x-value from the graph and demonstrating that the equation from part (q) holds for that value of x.
Answer:
For example, sin\(\left(-\frac{3 \pi}{4}\right)\) = \(\frac{\sqrt{2}}{2}\) and sin \(\left(\frac{3 \pi}{4}\right)\) = \(\frac{\sqrt{2}}{2}\), so sin\(\left(-\frac{3 \pi}{4}\right)\) = -sin\(\left(\frac{3 \pi}{4}\right)\).

s. Is the sine function an odd function, even function, or neither? Use the identity from part (q) to explain.
Answer:
The sine function is an odd function because sin(-x) = -sin(x) and because the graph is symmetric with respect to the origin.

t. Describe the x-intercepts of the graph of the sine function.
Answer:
The graph of the sine function has x-intercepts at all x-values such that x = nπ, where n is an integer.

u. Describe the end behavior of the sine function.
Answer:
As x increases to ∞ or as x decreases to -∞, the sine function cycles between the values of -1 and 1.

Exploratory Challenge 2.
Consider the function g(x) = cos(x) where x Is measured in radians.
Graph g(x) = cos(x) on the interval [-π, 5π] by constructing a table of values. Include all intercepts, relative maximum points, and relative minimum points. Then, use the graph to answer the questions that follow.


a. Using one of your colored pencils, mark the point on the graph at each of the following pairs of x-values.
x = –\(\frac{\pi}{2}\) and x = –\(\frac{\pi}{2}\) + 2π
x = π and x = π + 2π
x = \(\frac{7 \pi}{4}\) and x = \(\frac{7 \pi}{4}\) + 2π
Answer:

b. What can be said about the y-values for each pair of x-values marked on the graph?
Answer:
For each pair of x-values, the y-values are the same.

c. Will this relationship hold for any two x-values that differ by 2π? Explain how you know.
Answer:
Yes. Since the sine function repeats every 2π units, then the relationship described in part (b) will hold for any two x-values that differ by 2π.

d. Based on these results, make a conjecture by filling in the blank below.
For any real number x, cos(x + 2π) = _______ .
Answer:
cos(x + 2π) = cos(x)

e. Test your conjecture by selecting another x-value from the graph and demonstrating that the equation from part (d) holds for that value of x.
Answer:
cos (0) = cos(0 + 2π) = 1 (Answers will vary.)

f. How does the conjecture in part (d) support the claim that the cosine function is a periodic function?
Answer:
Like the sine function, the cosine function repeats every 2π units because 2π radians is one full turn. Thus, if we rotate the Initial ray through x + 2π radians, the terminal ray is in the same position as if we had rotated by x radians.

g. Use this identity to evaluate cos\(\left(\frac{9 \pi}{4}\right)\)
Answer:
cos\(\left(\frac{9 \pi}{4}\right)\) = cos(\(\frac{\pi}{4}\) + 2π) = cos\(\left(\frac{\pi}{4}\right)\) = \(\frac{\sqrt{2}}{2}\)

h. Using one of your colored pencils, mark the point on the graph at each of the following pairs of x-values.
x = –\(\frac{\pi}{4}\) and x = –\(\frac{\pi}{4}\) + π
x = 2π and x = 2π + π
x = \(\frac{5 \pi}{2}\) and x = \(\frac{5 \pi}{2}\) + π
Answer:

i. What can be said about the y-values for each pair of x-values marked on the graph?
Answer:
For each pair of x-values, the y-values have the same magnitude but opposite sign.

j. Will this relationship hold for any two x-values that differ by π? Explain how you know.
Answer:
Yes. Since rotating by an additional π radians produces a point in the opposite quadrant with the same reference angle, the sine of the two numbers will have the same magnitude and opposite sign.

k. Based on these results, make a conjecture by filling in the blank below.
For any real number x, cos(x + π) = _________ .
Answer:
cos(x + π) = -cos(x)

i. Test your conjecture by selecting another x-value from the graph and demonstrating that the equation from part (k) holds for that value of x.
Answer:
cos (3π) = cos(2π + π) = -cos(2π) = -1

m. Is the following statement true or false? Use the conjecture from (k) to explain your answer.
cos\(\left(\frac{5 \pi}{3}\right)\) = -cos\(\left(\frac{2 \pi}{3}\right)\)
Answer:
This statement is true: cos\(\left(\frac{5 \pi}{3}\right)\) = cos(\(\frac{2 \pi}{3}\) + π) = -cos\(\left(\frac{2 \pi}{3}\right)\).

n. Using one of your colored pencils, mark the point on the graph at each of the following pairs of x-values.
x = –\(\frac{3 \pi}{4}\) and x = \(\frac{3 \pi}{4}\)
x = -π and x = π
Answer:

o. What can be said about the y-values for each pair of x-values marked on the graph?
Answer:
For each pair of x-values, the y-values have the same magnitude but with the opposite sign.

p. Will this relationship hold for any two x-values with the same magnitude and same sign? Explain how you know.
Answer:
Yes. If rotation by x radians produces the point (a, b) on the unit circle, then rotation by -x radians will produce a point (a, -b) on the unit circle.

q. Based on these results, make a conjecture by filling in the blank below.
For any real number, cos(-x) = _________.
Answer:
cos(-x) = cos(x)

r. Test your conjecture by selecting another x-value from the graph and demonstrating that the identity is true for that value of x.
Answer:
cos(-2π) = cos(2π) = 1

s. Is the cosine function an odd function, even function, or neither? Use the identity from part (n) to explain.
Answer:
The cosine function is an odd function because cosin(-x) = cos(x) and because the graph is symmetric with respect to the origin.

t. Describe the x-intercepts of the graph of the sine function.
Answer:
The graph of the sine function has x-intercepts at all x-values such that x = \(\frac{\pi}{2}\) + nπ, where n is an integer.

u. Describe the end behavior of g(x) = cos(x).
Answer:
As x increases to ∞ or as x decreases to -∞, the cosine function cycles between the values of -1 and 1.

Exploratory Challenge 3
Graph both f(x) sin(x) and g(x) = cos(x) on the graph below. Then, use the graphs to answer the questions that follow.

a. List ways in which the graphs of the sine and cosine functions are alike.
Answer:
Both functions are periodic and have a period of 2π. Both functions have a domain of all real numbers and a range of [-1,1]. Both functions cycle between -1 and 1 as x increases to ∞ or as x decreases to -∞.
Both have similar identities such as sin(x + 2π) = sin(x) and cos(x + 2π) = cos(x).

b. List ways in which the graphs of the sine and cosine functions are different.
Answer:
We stated above that f(x) = sin(x) is an odd function, and g(x) = cos(x) is an even function. Where the sine function is at a maximum or minimum point, the cosine function has an x-intercept and vice versa.

c. What type of transformation would be required to make the graph of the sine function coincide with the graph of the cosine function?
Answer:
A horizontal shift

d. What is the smallest possible horizontal translation required to make the graph of f(x) = sin(x) coincide with the graph of g(x) = cos(x)?
Answer:
A horizontal shift \(\frac{\pi}{2}\) units to the left

e. What is the smallest possible horizontal translation required to make the graph of g(x) = cos(x) coincide with the graph of f(x) = sin(x)?
Answer:
A horizontal shift \(\frac{\pi}{2}\) units to the right

f. Use your answers from parts (d) and (e) to fill in the blank below.
For any real number x, _______ = cos (x – \(\frac{\pi}{2}\)).
For any real number x, ________= sin (x + \(\frac{\pi}{2}\)).
Answer:
sin(x) = cos (x – \(\frac{\pi}{2}\))
cos(x)= sin (x + \(\frac{\pi}{2}\))