Engage NY Eureka Math Algebra 2 Module 1 Mid Module Assessment Answer Key
Eureka Math Algebra 2 Module 1 Mid Module Assessment Answer Key
Question 1.
Geographers sit at a café discussing their field work site, which is a hill and a neighboring riverbed. The hill is approximately 1,050 feet high, 800 feet wide, with peak about 300 feet east of the western base of the hill. The river is about 400 feet wide. They know the river is shallow, no more than about 20 feet deep.
They make the following crude sketch on a napkin, placing the profile of the hill and riverbed on a coordinate system with the horizontal axis representing ground level.
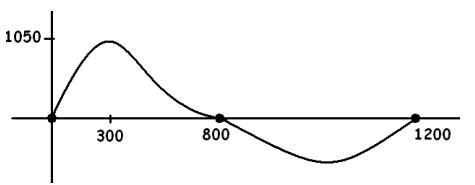
The geographers do not have any computing tools with them at the café, so they decide to use pen and paper to compute a cubic polynomial that approximates this profile of the hill and riverbed.
a. Using only a pencil and paper, write a cubic polynomial function H that could represent the curve shown (here, x represents the distance, in feet, along the horizontal axis from the western base of the hill, and H(x) is the height, in feet, of the land at that distance from the western base). Be sure that your formula satisfies H(300) = 1050.
Answer:
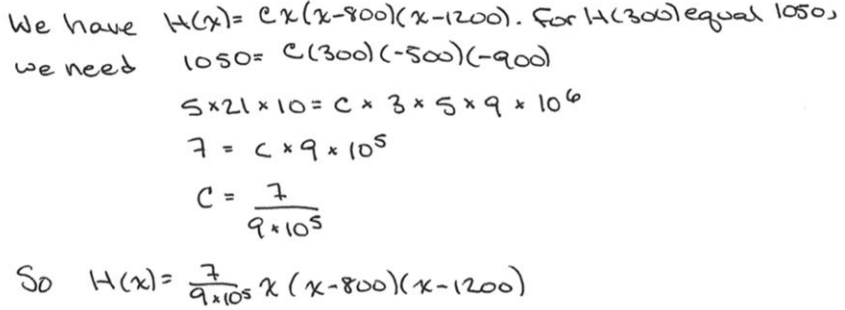
b. For the sake of convenience, the geographers make the assumption that the deepest point of the river is halfway across the river (recall that the river is no more than 20 feet deep). Under this assumption, would a cubic polynomial provide a suitable model for this hill and riverbed? Explain.
Answer:
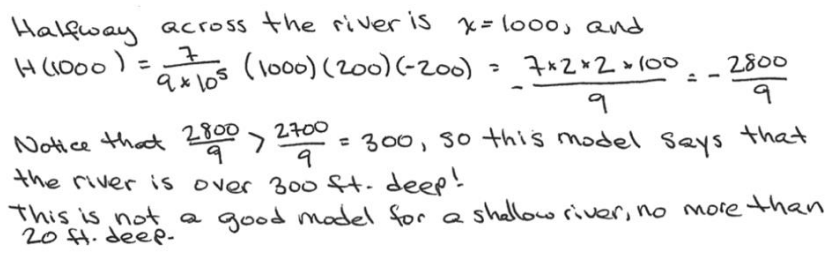
Question 2.
Luke notices that by taking any three consecutive integers, multiplying them together, and adding the middle number to the result, the answer always seems to be the middle number cubed.
For example:
3 × 4 × 5 + 4 = 64 = 43
4 × 5 × 6 + 5 = 125 = 53
9 × 10 ×11 + 10 = 1000 = 103
a. To prove his observation, Luke writes (n + 1) (n + 2) (n + 3) + (n + 2). What answer is he hoping to show this expression equals?
Answer:
(n + 2)3
b. Lulu, upon hearing of Luke’s observation, writes her own version with n as the middle number. What does her formula look like?
Answer:
(n – 1) n(n + 1) + n = n3
c. Use Lulu’s expression to prove that adding the middle number to the product of any three consecutive numbers is sure to equal that middle number cubed.
Answer:
We need to show (n – 1) n (n + 1) equals n3
Now (n – 1) n (n + 1) + n = n (n – 1) (n + 1) + n
= n (n2 – 1) + n
= n3 – n + n
= n3
It does !
Question 3.
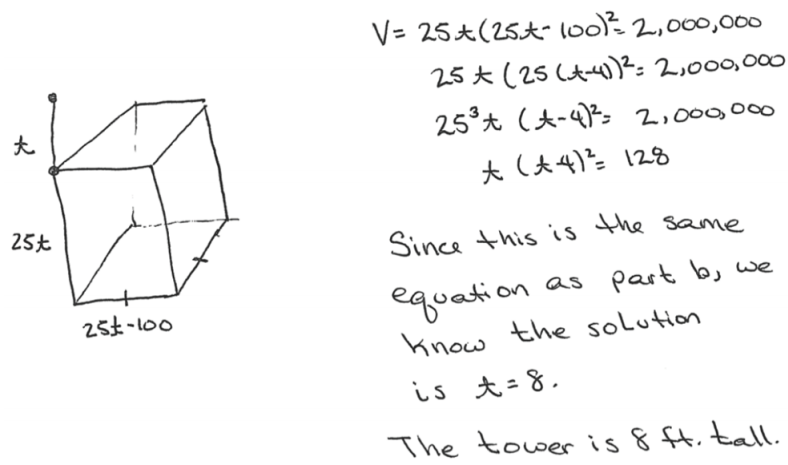
A cookie company packages its cookies in rectangular prism boxes designed with square bases that have both a length and width of 4 inches less than the height of the box.
a. Write a polynomial that represents the volume of a box with height x inches.
Answer:
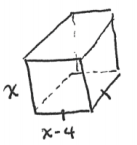
V = x(x – 4)2
b. Find the dimensions of the box if its volume is 128 cubic inches.
Answer:
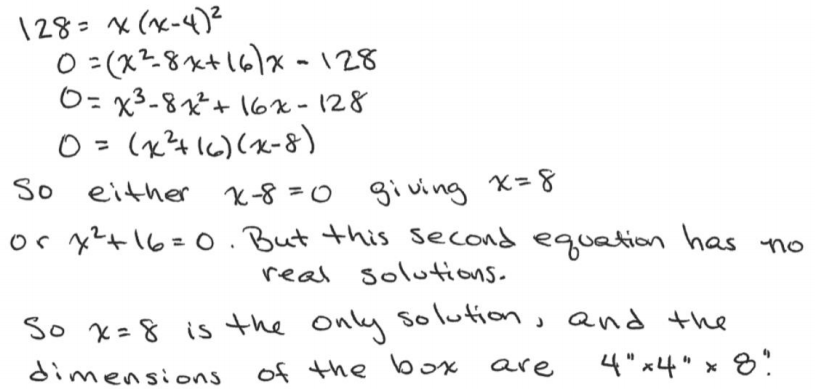
c. After solving this problem, Juan was very clever and invented the following strange question:
A building, in the shape of a rectangular prism with a square base, has on its top a radio tower. The building is 25 times as tall as the tower, and the side-length of the base of the building is 100 feet less than the height of the building, If the building has a volume of 2 million cubic feet, how tall is the tower?
Solve Juan’s problem.
Answer: