Eureka Math Algebra 2 Module 2 Lesson 5 Answer Key

Engage NY Eureka Math Algebra 2 Module 2 Lesson 5 Answer Key

Eureka Math Algebra 2 Module 2 Lesson 5 Opening Exercise Answer Key

a. Suppose that a group of 360 coworkers pool their money, buying a single lottery ticket every day with the understanding that if any ticket is a winning ticket, the group will split the winnings evenly, and they will donate any leftover money to the local high school. Using this strategy, if the group wins $1,000, how much money will be donated to the school?
Answer:
Since $1, 000 = $2(360) + $280, each coworker wins $2, and the local school receives the leftover $280.

b. What if the winning ticket is worth $250, 000? Using the same plan as in part (a), how much money will be donated to the school?
Answer:
Since $250,000 = $694(360) + $160, each coworker wins $694, and the school receives the leftover $160.

c. What if the winning ticket is worth $540,000? Using the same plan as in part (a), how much money will be donated to the school?
Answer:
Since $540,000 = $1, 500(360) + $0, each coworker wins $1, 500, and the school receives nothing.

Eureka Math Algebra 2 Module 2 Lesson 5 Exercise Answer Key

Exercise 1.
Find cos(405°) and sin(405°). Identify the measure of the reference angle.
Answer:
Since 405 = 360 + 45, and a 45° rotation places the terminal ray in the first quadrant, the reference angle measures 45°. Then, we have cos(405°) = cos(45°) = \(\frac{\sqrt{2}}{2}\), and sin(405°) = sin(45°) = \(\frac{\sqrt{2}}{2}\)

Exercise 2.
Find cos(840°) and sin(840°). Identify the measure of the reference angle.
Answer:
Since 840 = 2(360) + 120, and a 120° rotation places the terminal ray in the second quadrant, the reference angle measures 60°. Then, we have cos(840°) = – cos(60°) = –\(\frac{1}{2}\) , and sin(840°) = sin(60°) = \(\frac{\sqrt{3}}{2}\).

Exercise 3.
Find cos(1680°) and sin(1680°). Identify the measure of the reference angle.
Answer:
Since 1680 = 4(360) + 240, and a 240° rotation places the terminal ray in the third quadrant, the reference angle measures 60°. Then, we have cos(840°) = -cos(60°) = –\(\frac{1}{2}\), and sin(840°) = -sin(60°) = –\(\frac{\sqrt{3}}{2}\)

Exercise 4.
Find cos(2115°) and sin(2115°). Identify the measure of the reference angle.
Answer:
Since 2115 = 5(360) + 315, and a 315° rotation places the terminal ray in the fourth quadrant, the reference angle measures 45°. Then, we have cos(2115°) = cos(45°) = \(\frac{\sqrt{2}}{2}\) and sin(2115°) = – sin(45°) = –\(\frac{\sqrt{2}}{2}\)

Exercise 5.
Find cos(720 030°) and sin(720 030°). Identify the measure of the reference angle.
Answer:
Since 720 030 = 2000(360) + 30, and a 30° rotation places the terminal ray in the first quadrant, the reference angle measures 30°. Then, we have cos(720 030°) = cos(30°) = \(\frac{\sqrt{3}}{2}\), and sin(720 0300) = sin(30°) = \(\frac{1}{2}\)

Exercise 6.
Find cos(-30°) and sin(-30°). Identify the measure of the reference angle.
Answer:
Since a -30° rotation places the terminal ray in the fourth quadrant, the reference angle measures 30°. Then, we
have cos(-30°) = cos(30°) = \(\frac{\sqrt{3}}{2}\), and sin(-30°) = – sin(30°) = – \(\frac{1}{2}\).

Exercise 7.
Find cos(-135°) and sin(-135°). Identify the measure of the reference angle.
Answer:
Since the terminal ray of a -135° rotation aligns with the terminal ray of a 225° rotation in the third quadrant, the reference angle measures 45°. Then, we have cos(-135°) = – cos(45°) = –\(\frac{\sqrt{2}}{2}\), and sin(-135°) = – sin(45°) = –\(\frac{\sqrt{2}}{2}\).

Exercise 8.
Find cos(-1320°) and sin(-1320°). Identify the measure of the reference angle.
Answer:
Since the terminal ray of a -1320° rotation aligns with the terminal ray of a 120° rotation in the second quadrant, the reference angle measures 60°. Then, we have cos(-1320°) = -cos(60°) = –\(\frac{1}{2}\) and sin(-1320°) = sin(60°) = \(\frac{\sqrt{3}}{2}\).

Exercise 9.
Find cos(-2205°) and sin(-2205°). Identify the measure of the reference angle.
Answer:
Since the terminal ray of a – 2205° rotation aligns with the terminal ray of a -45° rotation in the fourth quadrant, the reference angle measures 45°. Then, we have cos(-2205°) = cos(45°) = \(\frac{\sqrt{2}}{2}\), and sin(-2205°) = -sin(45°) = –\(\frac{\sqrt{2}}{2}\)

Exercise 10.
Find cos(-2835°) and sin(-2835°). Identify the measure of the reference angle.
Answer:
Since the terminal ray of a -2835° aligns with the terminal ray of a 45° rotation in the first quadrant, the reference angle measures 45°. Then, we have
cos(-2835°) = -cos(45°) = \(\frac{\sqrt{2}}{2}\), and sin(-2835°) = sin(45°) = \(\frac{\sqrt{2}}{2}\).

Eureka Math Algebra 2 Module 2 Lesson 5 Discussion Answer Key

Discussion
Case 1: What about the values of the sine and cosine function of other amounts of rotation that produce a terminal ray along the positive x-axis, such as 1080°?

Our definition of a reference angle is the angle formed by the terminal ray and the x-axis, but our terminal ray lies along the x-axis, so the terminal ray and the x-axis form a zero angle.

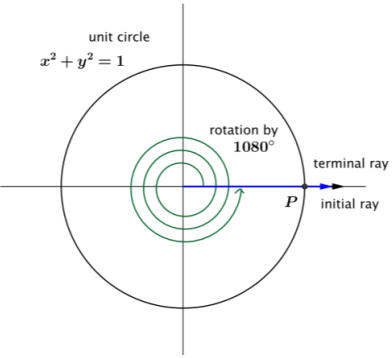
How would we assign values to cos(1080°) and sin(1080°)?
Answer:
Use the coordinates of point P, which are (1, 0). Then, cos(1080°) = 1, and sin(1080°) = 0.

What if we rotated around 240 00°, which is 400 turns? What are cos(24000°) and sin(24000°)?
Answer:
The terminal ray is the same as it was for 0°, so the intersection point P has coordinates (1, 0). Thus, cos(24000°) = 1, and sin(24000°) = 0.

State a generalization of these results:
If θ = n ∙ 360, for some integer n, then cos(θ°) = ______, and sin(θ°) = _______.
Answer:
If θ = n ∙ 360, for some integer n, then cos(θ°) = 1, and sin(θ°) = 0.

Case 2: What about the values of the sine and cosine function of other amounts of rotation that produce a terminal ray along the negative x-axis, such as 540°?

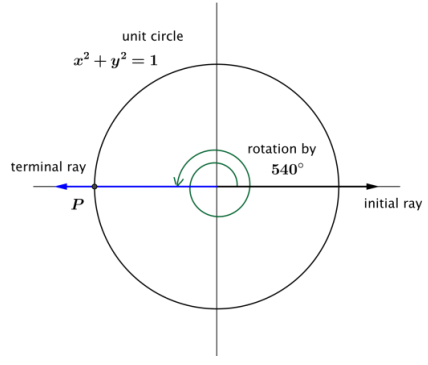
How would we assign values to cos(540°) and sin(540°)? unit circle
Answer:
Use the coordinates of point P, which are (- 1, 0). Then cos(540°) = – 1, and sin(540°) = 0.

What are the values of cos(900°) and sin(900°)? How do terminal ray
you know?
Answer:
Since the terminal ray of rotation by 900° lies along the negative x-axis, it coincides with the terminal ray of rotation by 540°. Thus, the coordinates of the intersection point P are (-1, 0), and we have cos(900°) = – 1, and sin(900°) = 0.

State a generalization of these results:
If θ = n ∙ 360 + 180, for some integer n, then cos(θ°) = ____ and sin(θ°) = ____.
Answer:
If θ = n ∙ 360 + 180,for some integer n, then cos(θ°) = – 1, and sin(θ°) = 0.

Case 3: What about the values of the sine and cosine function for rotations that are 90° more than a number of full turns,

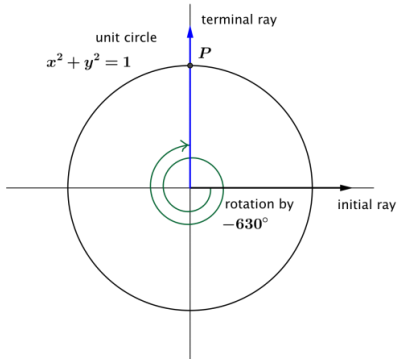
such as -630°? How would we assign values to cos(-630°), and sin(-630°)?
Answer:
Use the coordinates of point P, which are (0, 1). Then, cos(-630°) = 0, and sin(-630°) = 1.

Can we generalize to any rotation that produces a terminal ray along the positive y-axis?
Answer:
Yes

State a generalization of these results:
If θ = n ∙ 360 + 90, for some integer n, then cos(θ°) = ____, and sin(θ°) = _____.
Answer:
If θ = n ∙ 360 + 90, for some integer n, then cos(θ°) = 0, and sin(θ°) = 1.

Case 4: What about the values of the sine and cosine function for rotations whose terminal ray lies along the negative y-axis, such as -810°?

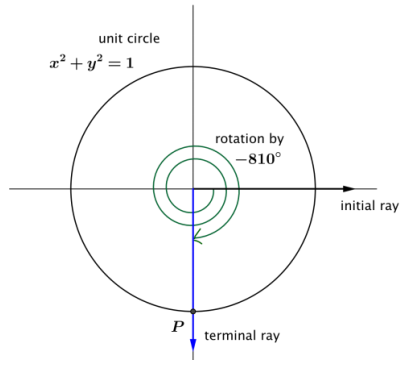
How would we assign values to cos(-810°) and sin(-810°)?
Answer:
Use the coordinates of point P, which are (0, – 1). Then, cos(- 810°) = 0, and sin(- 810°) = – 1.

Can we generalize to any rotation that produces a terminal ray along the negative y-axis?
Answer:
Yes

State a generalization of these results:
If θ = n ∙ 360 + 270, for some integer n, then, cos(θ°) = _____, and sin(θ°) = ____
Answer:
If θ = n ∙ 360 + 270,for some integer n, then cos(θ°) = 0, and sin(θ°) = – 1.

Eureka Math Algebra 2 Module 2 Lesson 5 Problem Set Answer Key

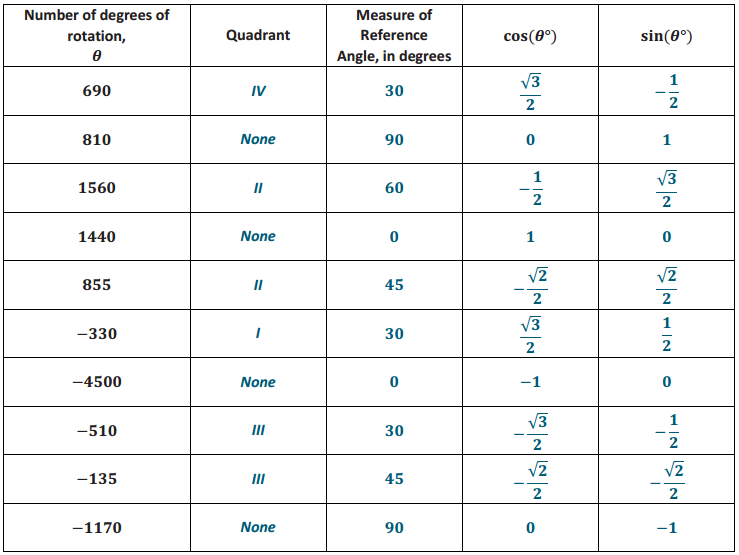
Question 1.
Fill in the chart. Write in the measures of the reference angles and the values of the sine and cosine functions for the indicated values of θ.

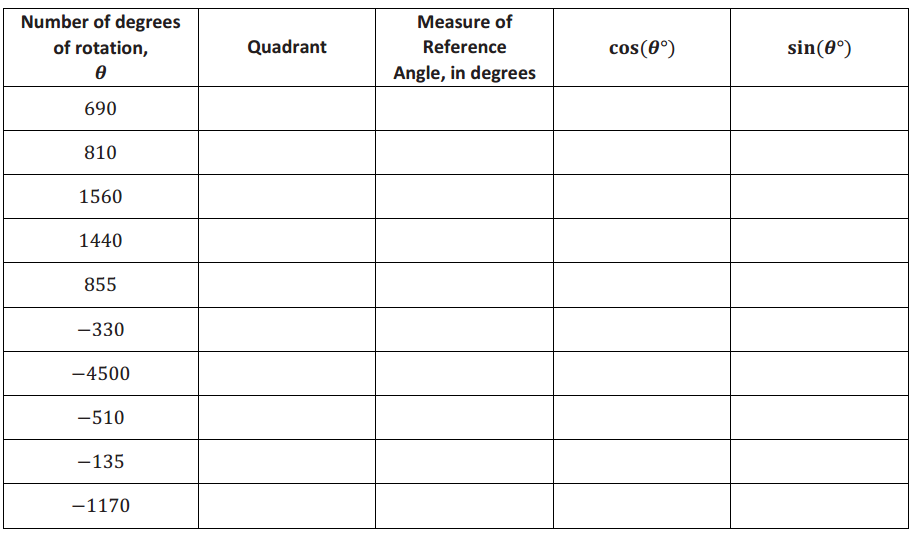
Answer:

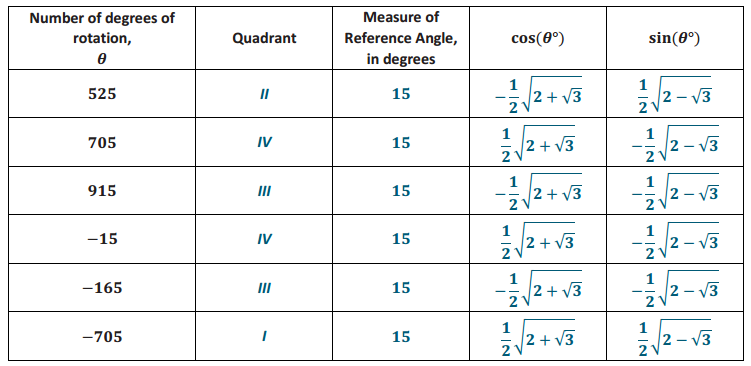
Question 2.
Using geometry, Jennifer correctly calculated that sin(15°) = \(\frac{1}{2} \sqrt{2-\sqrt{3}}\) Based on this information, fill in the chart:

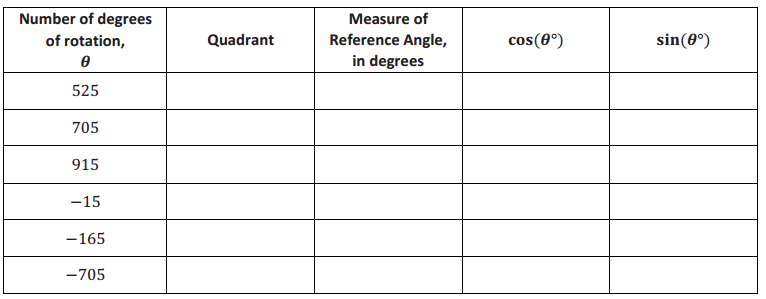
Answer:

Question 3.
Suppose θ represents a number of degrees of rotation and that sin(θ°) = 0. 5. List the first six possible positive values that θ can take.
Answer:
30, 150, 390, 510, 750, 870

Question 4.
Suppose θ represents a number of degrees of rotation and that sin(θ°) = – 0.5. List six possible negative values that θ can take.
Answer:
– 30, -150, -390, -510, -750, -870

Question 5.
Suppose θ represents a number of degrees of rotation. Is it possible that cos(θ° ) = \(\frac{1}{2}\) and sin(θ°) = \(\frac{1}{2}\)?
Answer:
No. If cos(θ°) = \(\frac{1}{2}\) and sin(θ°) = \(\frac{1}{2}\) then the coordinates of point P are \(\left(\frac{1}{2}, \frac{1}{2}\right)\) but this point doesn’t lie on the unit circle.

Question 6.
Jane says that since the reference angle for a rotation through – 765° has measure 45°, then cos(-765°) = cos(45°), and sin(-765°) = sin(45°). Explain why she is or is not correct.
Answer:
Jane is wrong. Because the terminal ray of the rotated initial ray lies in the fourth quadrant, we know that the y-coordinate changes sign. Thus, cos(-765°) = cos(45°), but sin(-765°) = -sin(45°).

Question 7.
Doug says that since the reference angle for a rotation through 765° has measure 45°, then cos(765°) = cos(45°), and sin(765°) = sin(45°). Explain why he is or is not correct.
Answer:
Doug’s conclusion is true, but his logic may be faulty. The reason cos(765°) = cos(45°) and sin(765°) = sin(45°) is that the terminal angle of the rotated ray lies in the first quadrant.

Eureka Math Algebra 2 Module 2 Lesson 5 Exit Ticket Answer Key

Question 1.
Calculate cos(480°) and sin(480°).
Answer:
Since 480° = 360° + 120°, the terminal ray of the rotated initial ray ¡sin the 2^nd quadrant. The reference angle is a
60° angle, so we have cos(480°) = – cos(60°) = –\(\frac{1}{2}\) and sin(480°) = sin(60°) = \(\frac{\sqrt{3}}{2} \)

Question 2.
Explain how we calculate the sine and cosine functions for a value of θ so that 540 < θ < 630.
Answer:
Since 540 < θ < 630, the terminal ray is in the 3^rd quadrant. The reference angle is the angle formed by the terminal ray and the negative x-axis; let the reference angle have measure degrees. Thus, the sine and cosine of θ will be the opposite of the sine and cosine of : cos(θ°) = – cos(Φ°), and sin(θ°) = sin(Φ°).