Eureka Math Algebra 2 Module 1 Lesson 40 Answer Key

Engage NY Eureka Math Algebra 2 Module 1 Lesson 40 Answer Key

Eureka Math Algebra 2 Module 1 Lesson 40 Example Answer Key

Consider the polynomial P(x) = x³ + 3x² + x – 5 whose graph is shown to the right.

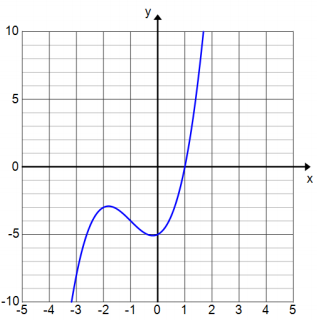
a. Looking at the graph, how do we know that there is only one real solution?
Answer:
The graph has only one x-intercept.

b. Is it possible for a cubic polynomial function to have no zeros?
Answer:
No. Since the opposite ends of the graph of a cubic function go in opposite directions, the graph must cross the x-axis at some point. Since the graph must have an x-intercept, the function must have a zero.

c. From the graph, what appears to be one solution to the equation x³ + 3x² + x – 5 = 0?
Answer:
The only real solution appears to be 1.

d. How can we verify that this value is a solution?
Answer:
Evaluate the function at 1; that is, verify that P(1) = 0.
P(1) = (1)³ + 3(1)² + 1 – 5 = 1 + 2 + 1 – 5 = 0

e. According to the remainder theorem, what Is one factor of the cubic expression x³ + 3x² + x – 5?
Answer:
(x – 1)

f. Factor out the expression you found in part (e) from x³ + 3x² + x – 5.
Answer:
Using polynomial division, we see that x³ + 3x² + x – 5 = (x – 1) (x² + 4x + 5).

g. What are all of the solutions to x³ + 3x² + x – 5 = 0?
Answer:
The quadratic equation x² + 4x + 5 = 0 has solutions – 2 – i and – 2 + i by the quadratic formula, so the original equation has solutions 1, – 2 – i, and -2 + i.

h. Write the expression x³ + 3x² + x – 5 in terms of linear factors.
Answer:
The factored form of the cubic expression is
x³ + 3x² + x – 5 = (x – 1) (x – (- 2 – i)) (x-(- 2 + i))
= (x – 1) (x + 2 + i) (x + 2 – i).

Example 2.
Consider the polynomial function P(x) = x⁴ – 3x³ + 6x² – 12x + 8, whose corresponding graph y = x⁴ – 3x³ + 6x² – 12x + 8 is shown to the right. How many zeros does P have?

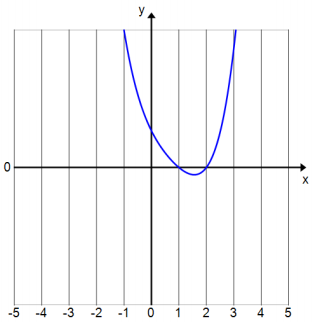
a. Part 1 of the fundamental theorem of algebra says that this equation will have at least one solution in the complex numbers. How does this align with what we can see in the graph to the right?
Answer:
Since the graph has 2 x-Intercepts, there appear to be 2 zeros to the function. We were guaranteed one zero, but we know there are at least two.

b. Identify one zero from the graph.
Answer:
One zero is 1. (The other is 2.)

c. Use polynomial division to factor out one linear term from the expression x⁴ – 3x³ + 6x² – 12x + 8.
Answer:
x⁴ – 3x³ + 6x² – 12x + 8 = (x – 1) (x³ – 2x² + 4x – 8)

d. Now we have a cubic polynomial to factor. We know by part 1 of the fundamental theorem of algebra that a polynomial function will have at least one real zero. What is that zero in this case?
Answer:
The original polynomial function had real zeros at 1 and 2, so the cubic function P(x) = x³ – 2x² + 4x – 8 has a zero at 2.

e. Use polynomial division to factor out another linear term of x⁴ – 3x³ + 6x² – 12x + 8.
Answer:
x⁴ – 3x³ + 6x² – 2x + 8 = (x – 1) (x³ – 2x² + 4x – 8) = (x – 1) (x – 2) (x² + 4)

f. Are we done? Can we factor this polynomial any further?
Answer:
At this point, we can see that x² + 4 = (x + 2i)(x – 2i), so
x⁴ – 3x³ + 6x² – 12x + 8 = (x – 1) (x – 2) (x + 2i) (x – 2i).

g. Now that the polynomial is in factored form, we can quickly see how many solutions there are to the original equation x⁴ – 3x³ + 6x²– 12x + 8 = 0.
Answer:
If x⁴ – 3x³ + 6x² – 12x + 8 = 0, then (x – 1) (x – 2) (x + 2i) (x – 2i) = 0, so the solutions are 1, 2, 2i and – 2i. So, the polynomial P has 4 zeros; 2 are real numbers, and 2 are complex numbers.

h. What if we had started with a polynomial function of degree 8?
Answer:
We would find the first zero and factor out a linear term, leaving a polynomial of degree 7. We would then find another zero, factor out a linear term, leaving a polynomial of degree 6. We would repeat this process until we had a quadratic polynomial remaining; then, we would factor that with the help of the quadratic formula. We would have 8 linear factors at the end of the process that correspond to the 8 zeros of the original function.

Eureka Math Algebra 2 Module 1 Lesson 40 Opening Exercise Answer Key

Write each of the following quadratic expressions as a product of linear factors. Verify that the factored form is equivalent.

a. x² + 12x +27
Answer:
(x + 3) (x + 9)

b. x² – 16
Answer:
(x + 4) (x – 4)

c. x² + 16
Answer:
(x + 4i) (x – 4i)

d. x² + 4x + 5
Answer:
(x + 2 + i) (x + 2 – i)

Eureka Math Algebra 2 Module 1 Lesson 40 Exercise Answer Key

Write each polynomial in terms of linear factors. The graph of y = x³ – 3x² + 4x – 12 is provided for Exercise 2.

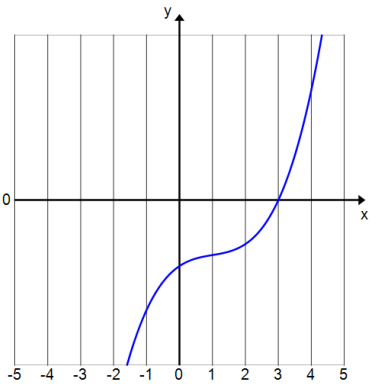
Exercise 1.
f(x) = x³ + 5x
Answer:
f(x) = x(x + i√5) (x – i√5)

Exercise 2.
g(x) = x³ – 3x² + 4x – 12
Answer:
g(x) = (x – 3) (x + 2i) (x – 2i)

Eureka Math Algebra 2 Module 1 Lesson 40 Problem Set Answer Key

Question 1.
Write each quadratic function below in terms of linear factors.
a. f(x) = x² – 25
Answer:
f(x) = (x + 5)(x – 5)

b. f(x) = x² + 25
Answer:
f(x) = (x + 5i) (x – 5i)

c. f(x) = 4x² + 25
Answer:
f(x) = (2x + 5i)(2x – 5i)

d. f(x) = x² – 2x + 1
Answer:
f(x) = (x – 1)(x – 1)

e. f(x) = x² – 2x + 4
Answer:
f(x) = (x – 1 + i√3) (x – 1 – i√3)

Question 2.
Consider the polynomial function P(x) = (x² + 4) (x² + 1) (2x + 3) (3x – 4).
a. Express P in terms of linear factors.
Answer:
P(x) = (x + 2i) (x – 2i) (x + i) (x – i) (2x + 3) (3x – 4)

b. Fill in the blanks of the following sentence.
The polynomial P has degree _____________ and can, therefore, be written in terms of _________ linear factors. The function P has __________ zeros. There are __________ real zeros and ______ complex zeros. The graph of y = P(x) has _______ x-intercepts.
Answer:
The polynomial P has degree   6    and can, therefore, be written in terms of   6    linear factors. The function P has   6    zeros. There are   2    real zeros and   4    complex zeros. The graph of y =P(x) has   2    x-intercepts.

Question 3.
Express each cubic function below in terms of linear factors.
a. f(x) = x³ – 6x² – 27x
Answer:
f(x) = x(x – 9) (x + 3)

b. f(x) = x³ – 16x²
Answer:
f(x) = x²(x – 16)

c. f(x) = x³ + 16x
Answer:
f(x) = x(x + 4i)(x – 4i)

Question 4.
For each cubic function below, one of the zeros is given. Express each cubic function in terms of linear factors.
a. f(x) = 2x³ – 9x² – 53x – 24; f(8) = 0
Answer:
f(x) = (x – 8) (2x + 1) (x + 3)

b. f(x) = x³ + x² + 6x + 6; f(-1) = 0
Answer:
f(x) = (x + 1) (x + i√6) (x – i√6)

Question 5.
Determine if each statement is always true or sometimes false. If it is sometimes false, explain why it is not always true.
a. A degree 2 polynomial function will have two linear factors.
Answer:
Always true

b. The graph of a degree 2 polynomial function will have two x-intercepts.
Answer:
False. It is possible for the solutions to a degree 2 polynomial to be complex, in which case the graph would not cross the x-axis. It is also possible for the graph to have only one x-intercept if the vertex lies on the x axis.

c. The graph of a degree 3 polynomial function might not cross the x-axis.
Answer:
False. A degree 3 polynomial must cross the x-axis at least one time.

d. A polynomial function of degree n can be written in terms of n linear factors.
Answer:
Always true

Question 6.
Consider the polynomial function f(x) = x⁶ – 9x³ + 8.
a. How many linear factors does x⁶ – 9x³ + 8 have? Explain.
Answer:
Since the degree is 6, the polynomial must have 6 linear factors.

b. How is this information useful for finding the zeros of f?
Answer:
We know that the function has 6 zeros since there are 6 linear factors. Each factor corresponds to a zero of the function.

c. Find the zeros off. (Hint: Let Q = x³. Rewrite the equation in terms of Q to factor.)
Answer:
1, 2, – 1 + i√3, – 1 – i√3, \(\frac{-1+i \sqrt{3}}{2}\), \(\frac{-1-i \sqrt{3}}{2}\)

Question 7.
Consider the polynomial function P(x) = x⁴ – 6x³ + 11x⁴ – 18.

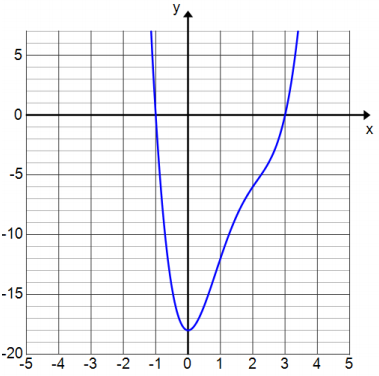
a. Use the graph to find the real zeros of P.
Answer:
The real zeros are – 1 and 3.

b. Confirm that the zeros are correct by evaluating the function P at those values.
Answer:
P(- 1) = 0 and P(3) = 0

c. Express P in terms of linear factors.
Answer:
P(x) = (x + 1) (x – 3) (x – (2 + i√2)) (x – (2 – i√2))

d. Find all zeros of P.
Answer:
– 1, 3, 2 – i√2, 2 + i√2

Question 8.
Penny says that the equation x³ – 8 = 0 has only one solution, x = 2. Use the fundamental theorem of algebra to explain to her why she is incorrect.
Answer:
Because x³ – 8 is a degree 3 polynomial, the fundamental theorem of algebra guarantees that x³ – 8 can be written as the product of three linear factors; therefore, the corresponding equation has 3 solutions. One of the 3 solutions is 2. We know that 2 cannot be the only solution because (x – 2)(x – 2)(x – 2) ≠ x³ – 8.

Question 9.
Roger says that the equation x² – 12x + 36 = 0 has only one solution, 6. Regina says Roger is wrong and that the fundamental theorem of algebra guarantees that a quadratic equation must have two solutions. Who is correct and why?
Answer:
Roger is correct. While the fundamental theorem of algebra guarantees that a quadratic polynomial can be written in terms of two linear factors, the factors are not necessarily distinct. We know that x² – 12x + 36 = (x – 6)(x – 6), so the equation x² – 12x + 36 = 0 has only one solution, which is 6.

Eureka Math Algebra 2 Module 1 Lesson 40 Exit Ticket Answer Key

Consider the degree 5 polynomial function P(x) = x⁵ – 4x³ + 2x² + 3x – 5 whose graph ¡s shown below. You do not need to factor this polynomial to answer the questions below.

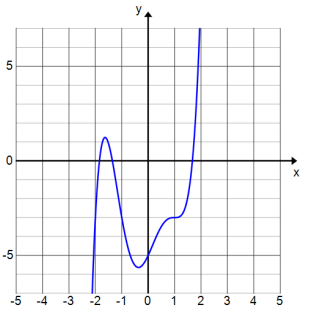
Question 1.
How many linear factors is P guaranteed to have? Explain.
Answer:
The polynomial expression must have 5 linear factors. The fundamental theorem of algebra guarantees that a polynomial function can be written in terms of linear factors and must have the same number of linear factors as its degree.

Question 2.
How many zeros does P have? Explain.
Answer:
Since P can be written in terms of 5 linear factors, the equation P must have 5 zeros (counted with multiplicity).

Question 3.
How many real zeros does P have? Explain.
Answer:
The graph crosses the x-axis 3 times, which means that three of the zeros are real numbers.

Question 4.
How many complex zeros does P have? Explain.
Answer:
Since P must have 5 total zeros and only 3 of them are real, there must be 2 complex zeros.