Eureka Math Algebra 2 Module 1 Lesson 37 Answer Key

Engage NY Eureka Math Algebra 2 Module 1 Lesson 37 Answer Key

Eureka Math Algebra 2 Module 1 Lesson 37 Example Answer Key

Example 1.
Addition with Complex Numbers
Compute (3 + 4i) + (7 – 20i).
Answer:
(3 + 4i) + (7 – 20i) = 3 + 4i + 7 – 20i = (3 + 7) + (4 – 20)i = 10 – 16i

Example 2.
Subtraction with Complex Numbers
Compute (3 + 4i) – (7 – 20i).
Answer:
(3 + 4i) – (7 – 20i) = 3 + 4i – 7 + 20i = (3 – 7) + (4 + 20)i = – 4 + 20i

Example 3.
Multiplication with Complex Numbers
Compute (1 + 2i) (1 – 2i).
Answer:
(1 + 2i) (1 – 2i) = 1 + 2i – 2i – 4i² – 2 + 4i + 5
= 1 + 0 – 4(-1)
= 1 + 4
= 5

Example 4.
Multiplication with Complex Numbers
Verify that -1 + 2i and -1 – 2i are solutions to x² + 2x + 5 = 0.
Answer:
– 1 + 2i:
(- 1 + 2i)² + 2(-1 + 2i) + 5 = 1 – 4i + 4i² – 2 + 4i + 5
= 4i² – 4i + 4i + 1 – 2 + 5
= – 4 + 0 + 4
= 0

– 1 – 2i:
(- 1 – 2i)² + 2(- 1 – 2i) + 5 = 1 + 4i + 4i² – 2 – 4i + 5
= 4i² + 4i – 4i + 1 – 2 + 5
= – 4 + 0 + 4
= 0
So, both complex numbers – 1 – 2i and – 1 + 21 are solutions to the quadratic equation x² + 2x + 5 = 0.

Eureka Math Algebra 2 Module 1 Lesson 37 Opening Exercise Answer Key

Solve each equation for x.

a. x – 1 = 0
Answer:
1

b. x + 1 = 0
Answer:
– 1

c. x² – 1 = 0
Answer:
1, – 1

d. x² + 1 = 0
Answer:
No real solution

Eureka Math Algebra 2 Module 1 Lesson 37 Problem Set Answer Key

Question 1.
Locate the point on the complex plane corresponding to the complex number given in parts (a) – (b). On one set of axes, label each point by its identifying letter. For example, the point corresponding to 5 + 2i should be labeled a.
a. 5 + 2i
b. 3 – 2i ‘I
c. – 2 – 4i
d. – i
e. \(\frac{1}{2}\) + i
f. √2 – 3i
g. 0
h. \(-\frac{3}{2}+\frac{\sqrt{3}}{2}\)i

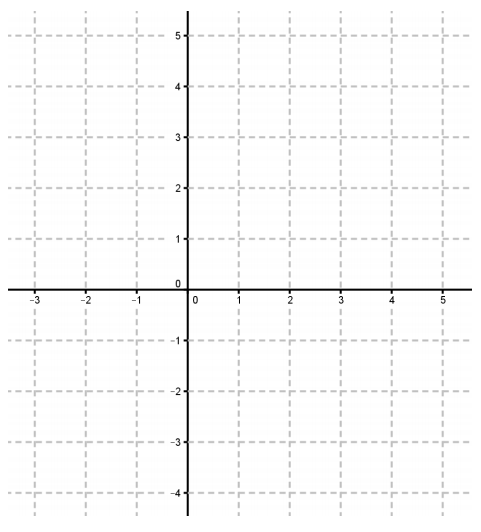
Answer:

Question 2.
Express each of the following in a + bi form.
a. (13 + 4i) + (7 + 5i)
Answer:
(13 + 7) + (4 + 5)i = 20 + 9i

b. (5 – i) – 2 (1 – 3i)
Answer:
5 – i – 2 + 6i = 3 + 5i

c. ((5 – i) – 2 (1 – 3i))²
Answer:
(3 + 5i)² = 9 + 30i + 25i²
= 9 + 30i + (- 25)
= – 16 + 30i

d. (3 – i) (4 + 7i)
Answer:
12 – 4i + 21i – 7i² = 12 + 17i – (-7)
= 19 + 17i

e. (3 – i) (4 + 7i) – ((5 – i) – 2(1 – 3i))
Answer:
(19 + 17i) – (3 + 5i) = (19 – 3) + (17 – 5)i
= 16 + 12i

Question 3.
Express each of the following in a + bi form.
a. (2 + 5i) + (4 + 3i)
Answer:
(2 + 5i) + (4 + 3i) = (2 + 4) + (5 + 3)i
= 6 + 8i

b. (- 1 + 2i) – (4 – 3i)
Answer:
(- 1 + 2i) – (4 – 3i) = – 1 + 2i – 4 + 3i
= – 5 + 5i

c. (4 + i) + (2 – i) – (1 – i)
Answer:
(4 + i) + (2 – i) – (1 – i) = 4 + i + 2 – i – 1 + i
= 5 + i

d. (5 + 3i) (3 + 5i)
Answer:
(5 + 3i) (3 + 5i) = 5 ∙ 3 + 3 ∙ 3i + 5 ∙ 5i + 3i ∙ 5i
= 15 + 9i + 25i + 15i²
= 15 + 34i – 15
= 0 + 34i
= 34i

e. – i(2 – i) (5 + 6i)
Answer:
– i(2 – i)(5 + 6i) = -i(10 – 5i + 12i – 6i²)
= – i(10 + 7i + 6)
= – i(16 + 7i)
= – 16i – 7²
= – 16i + 7
= 7 – 16i

f. (1 + i) (2 – 3i) + 3i(1 – i) – i
Answer:
(1 + i)(2 – 3i) + 3i(1 – L) – i = (2 + 2i – 3i – 3i²) + 3i – 3i² – i
= 2 + 2i – 3i + 3 + 3i + 3 – i
= 8 + i

Question 4.
Find the real values of x and y in each of the following equations using the fact that if a + bi = c + di, then a = c and b = d.
a. 5x + 3yi = 20 + 9i
Answer:
5x = 20
x = 4

3yi = 9i
y = 3

b. 2(5x + 9) = (10 – 3y)i
Answer:
2(5x + 9) + 0i = 0 +(10 – 3y)i
2(5x + 9) = 0
x = \(\frac{9}{5}\)

0i = (10 – 3y)i
10 – 3y = 0
y = \(\frac{10}{3}\)

c. 3(7 – 2x) – 5(4y – 3)i = x – 2(1 + y)i
Answer:
3(7 – 2x) = x
21 – 6x = x
21 = 7x
x = 3

– 5 (4y – 3)i = – 2(1 + y)i
– 5 (4y – 3) = – 2(1 + y)
– 20y + 15 = – 2 – 2y
17 = 18y
y = \(\frac{17}{18}\)

Question 5.
Since i² = – 1, we see that
i³ = i² ∙ i = – 1 ∙ i = – i
i⁴ = i² ∙ i² = – 1 ∙ – 1 = 1.
Plot i, i², i³, and i⁴ on the complex plane, and describe how multiplication by each rotates points in the complex plane.

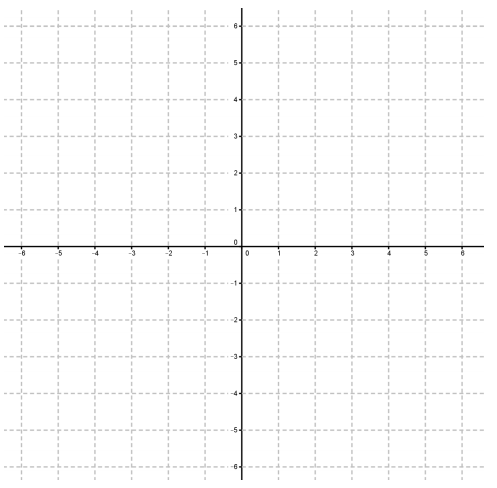
Answer:
Multiplying by i rotates points by 90° counterclockwise around (0, 0). Multiplying by i² = – 1 rotates points by 180° about (0, 0). Multiplying by t³ = – i rotates points counterclockwise by 270° about the origin, which is equivalent to rotation by 90° clockwise about the origin. Multiplying by i⁴ rotates points counter clockwise by 360°, which is equivalent to not rotating at all. The points i, i², i³, and i⁴ are plotted below on the complex plane.

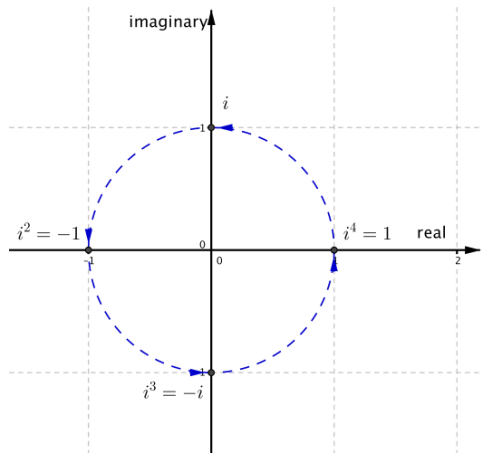
Question 6.
Express each of the following in a + bi form.
a. i⁵
Answer:
0 + i

b. i⁶
Answer:
– 1 + 0i

c. i⁷
Answer:
0 – i

d. i⁸
Answer:
1 + 0i

e. i¹⁰²
Answer:
– 1 + 0i
A simple approach is to notice that every 4 multiplications by i result in four 90° rotations, which takes i⁴ back to 1. Therefore, divide 102 by 4, which is 25 with remainder 2. So, 102 90° rotations is equivalent to 25 360° rotations and a 180° rotation, and thus i¹⁰² = – 1.

Question 7.
Express each of the following in a + bi form.
a. (1 + i)²
Answer/:
(1 + i) (1 + i) = 1 + i + i + i²
= 1 + 2i – 1
= 2i

b. (1 + i)⁴
Answer:
(1 + i)⁴ = ((1 + i)²)²
= (2i)²
= 4i²
= – 4

c. (1 + i)⁶
Answer:
(1 + i)⁶ = (1 + i)² (1 + i)⁴
= (2i) (- 4)
= – 8i

Question 8.
Evaluate x² – 6x when x = 3 – i.
Answer:
– 10

Question 9.
Evaluate 4x² – 12x when x = \(\)
Answer:
– 10

Question 10.
Show by substitution that \(\frac{5-i \sqrt{5}}{5}\) is a solution to 5x² – 10x + 6 = 0.
Answer:
\(5\left(\frac{5-i \sqrt{5}}{5}\right)^{2}\) – 10 \(\left(\frac{5-i \sqrt{5}}{5}\right)\) = \(\frac{1}{5}\) (5 – i√5) (5 – i√5) – 2(5 – i√5) + 6
= \(\frac{1}{5}\) (25 – 10i√5 + 5i²) – 2 (5 – i√5) + 6
= \(\frac{1}{5}\) (25 – 10i√5 – 5) – 2 (5 – i√5) + 6
= 5 – 2i√5 – 1 – 10 + 2i√5 + 6
= 0

Question 11.
a. Evaluate the four products below.
Evaluate √9 ∙ √4
Answer:
3 ∙ 2 = 6

Evaluate √9 ∙ √-4
Answer:
3 ∙ 2i = 6i

Evaluate √-9 ∙ √4.
Answer:
3i ∙ 2 = 6i

Evaluate √-9 ∙ √-4
Answer:
3i ∙ 2i = 6i² = – 6

b. Suppose a and b are positive real numbers. Determine whether the following quantities are equal or not equal.
Answer:
√a ∙ √b and √-a ∙ √-b
Answer:
not equal

√-a ∙ √b and √a ∙ √-b
Answer:
equal

Eureka Math Algebra 2 Module 1 Lesson 37 Exit Ticket Answer Key

Express the quantities below in a + bi form, and graph the corresponding points on the complex plane. If you use one
set of axes, be sure to label each point appropriately.
(1 + i) – (1 – i)
Answer:
(1 + i) – (1 – i) = 0 + 2i
= 2i

(1 + i) (1 – i)
Answer:
(1 + i) (1 – i) = 1 + i – i – i²
= 1 – i²
= 1 + 1
= 2 + 0i
= 2

i(2 – i) (1 + 2i)
Answer:
i(2 – i) (1 + 2i) = i(2 + 4i – i – 2i²)
= i(2 + 3i – 2(-1))
= i(2 + 3i + 2)
= i(4 + 3i)
= 4i + 3i²
= – 3 + 4i