Eureka Math Algebra 2 Module 1 Lesson 39 Answer Key

Engage NY Eureka Math Algebra 2 Module 1 Lesson 39 Answer Key

Eureka Math Algebra 2 Module 1 Lesson 39 Opening Exercise Answer Key

Rewrite each expression as a polynomial in standard form.

a. (x + i)(x – i)
Answer:
(x + i)(x – i) = x² + ix – ix – i²
= x² – i²
= x² – (-1)
= x² + 1

b. (x + 5i)(x – 5i)
Answer:
(x + 5i)(x – 5i) =x² + 5ix – 5ix – 25i²
= x² – 25i²
= x² – 25(- 1)
=x² + 25

c. (x – (2 + i))(x – (2 – i))
Answer:
(x – (2 + i))(x – (2 – 1)) = x² – (2 + i)x – (2 – i)x + [(2 + i)(2 – t)]
= x² – 2x – ix – 2x + ix + [4 – i²]
= x² – 4x + [4-(-1)]
= x² – 4x + 5

Eureka Math Algebra 2 Module 1 Lesson 39 Exercise Answer Key

Factor the following polynomial expression into products of linear terms.

Exercise 1.
x² + 9
Answer:
x² + 9 = (x + 3i) (x – 3i)

Exercise 2.
x² + 5
Answer:
x² + 5 = (x + i√5) (x – i√5)

Exercise 3.
Consider the polynomial P(x) = x⁴ – 3x² – 4.
a. What are the solutions to x⁴ – 3x² – 4 = 0?
Answer:
x⁴ – 3x² – 4 = 0
(x²)² – 3x² – 4 = 0
(x² + 1)(x² -4) = 0
(x + i) (x – i) (x + 2) (x – 2) = 0
The solutions are -i, i, -2, and 2.

b. How many x-intercepts does the graph of the equation y = x⁴ – 3x² – 4 have? What are the coordinates of the x-intercepts?
Answer:
The graph of y = x⁴ – 3x² – 4 has two x-intercepts: (-2, 0) and (2, 0).

c. Are solutions to the polynomial equation P(x) = 0 the same as the x-lntercepts of the graph of y = Justify your reasoning.
Answer:
No. Only the real solutions to the equation are x-intercepts of the graph. By comparing the graph of the polynomial in part (b) to the equation’s solutions from part (c), you can see that only the real number solutions to the equation correspond to the x-intercepts in the Cartesian plane.

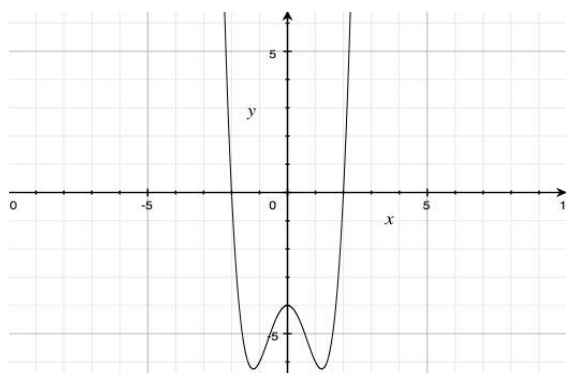
Exercise 4.
Write a polynomial P with the lowest possible degree that has the given solutions. Explain how you generated each answer.
a. – 2, 3, – 4i, 4i
Answer:
The polynomial P has two real zeros and two complex zeros. Since the two complex zeros are members of a conjugate pair, P may have as few as four total factors. Therefore, P has degree at least 4.
P(x) = (x + 2) (x – 3) (x + 4i) (x – 4i)
= (x² – x – 6) ( x² – 16i²)
= (x² – x – 6) (x² + 16)
= x⁴ – x³ – 6x² + 16x²– 1 6x – 96
= x⁴ – x³ + 10x² – 16x -96

b. – 1, 3i
Answer:
The polynomial P has one real zero and two complex zeros because complex zeros come in pairs. Since 3 i and – 3i form a conjugate pair, P has at least three total factors. Therefore, P has degree at least 3.
P(x) = (x + 1) (x – 3i) (x + 3i)
= (x + 1) (x² – 9i²)
= (x + 1) (x² + 9)
= x³ + x² + 9x + 9

c. 0, 2, 1+i, 1-i
Answer:
Since 1 + i and 1 – i are complex conjugates, P is at least a 4th degree polynomial.
P(x) = x(x – 2) (x – (1 + i)) (x – (1 – i))
= x(x – 2) [(x – 1) -i [(x – 1) + i]
= x(x -2) [(x – 1)² – i²]
= x(x – 2) [(x² – 2x + 1) + 1]
= x(x – 2) (x² – 2x + 2)
= x(x³ – 2x² + 2x – 2x² + 4x – 4)
= x (x³ – 4x² + 6x – 4)
= x⁴ – 4x³ + 6x² – 4x

d. √2, -√2, 3, 1 + 2i
Answer:
Since 1 + 2i is a complex solution to P(x) = 0, its conjugate, 1 – 2i, must also be a complex solution. Thus, P is at least a fifth-degree polynomial.
P(x) = (x – √2) (x + √2) (x – 3) (x – (1 + 2i)) (x – (1 – 2i))
= (x² – 2) (x – 3) [(x – 1) – 2i] [(x – 1) + 2i]
= (x² – 2) (x – 3) [(x – 1)² – 4i²]
= (x² – 2) (x – 3) [(x² – 2x + 1) + 4]
= (x² – 2) (x – 3) (x² – 2x + 5)
= (x³ – 3x² – 2x + 6) (x² – 2x + 5)
= x⁵ – 5x⁴ + 9x³ – 5x² – 22x + 30

e. 2i, 3 – i
Answer:
The complex conjugates of 2i and 3 – i are -2i and 3 + i, respectively. So, P is at least a fourth-degree polynomial.
P(x) = (x – 2i) (x + 2i)( x – (3 – i))(x – (3 + i))
= (x² – 4i²) [(x – 3) + i] [(x – 3) – i]
= (x² + 4) [(x – 3)² – i²]
= (x² + 4) [(x² – 6x + 9) + 1]
= (x² + 4) (x² – 6x + 10)
= x⁴ – 6x³ + 14x² – 24x + 40

Eureka Math Algebra 2 Module 1 Lesson 39 Problem Set Answer Key

Question 1.
Rewrite each expression in standard form.
a. (x + 3i) (x – 3i)
Answer:
x² + 3² = x² + 9

b. (x – a + bi) (x – (a + bi))
Answer:
(x – a + bi) (x – (a + bi)) = ((x – a) + bi) ((x – a) – bi)
= (x – a)² + b²
= x² – 2ax + a² + b²

c. (x + 2i)(x – i)(x + i)(x – 2i)
Answer:
(x + 2i) (x – 2i) (x + i) (x – i) = (x² + 2²)( x² + 1²)
= (x² + 4) (x² + 1)
= x⁴ + 5x² + 4

d. (x + i)² ∙ (x – i)²
Answer:
(x + i)(x – i) ∙ (x + i) (x – i) = (x² + 1) (x² + 1)
= x⁴ + 2x² + 1

Question 2.
Suppose in Problem 1 that you had no access to paper, writing utensils, or technology. How do you know that the expressions in parts (a)-(d) are polynomials with real coefficients?
Answer:
In part (a), the identity (x + ai) (x – ai) = x² + a² can be applied. Since the number a is real, the resulting polynomial will have real coefficients. The remaining three expressions can all be rearranged to take advantage of the conjugate pairs identity. In parts (c) and (d), regrouping terms will produce products of polynomial expressions with real coefficients, which will again have real coefficients.

Question 3.
Write a polynomial equation of degree 4 in standard form that has the solutions i, – i, 1, – 1.
Answer:
The first step is writing the equation in factored form:
(x + 1) (x – i) (x + 1) (x – 1) = 0.
Then, use the commutative property to rearrange terms and apply the difference of squares formula:
(x + i) (x – i) (x + 1) (x – 1) = (x² + 1) (x² – 1)
= x⁴ – 1.
So, the standard form of the equation ¡s
x⁴ – 1 = 0.

Question 4.
Explain the difference between x-intercepts and solutions to an equation. Give an example of a polynomial with real coefficients that has twice as many solutions as x-intercepts. Write it in standard form.
Answer:
The x-intercepts are the real solutions to a polynomial equation with real coefficients. The solutions to an equation can be real or not reaL The previous problem is an example of a polynomial with twice as many solutions than x intercepts. Or, we could consider the equation x⁴ – 6x³ + 13x² – 12x + 4 = 0, which has zeros of multiplicity 2 at both 1 and 2.

Question 5.
Find the solutions to x⁴ – 5x² – 36 = 0 and the x-intercepts of the graph of y = x⁴ – 5x² – 36.
Answer:
(x² + 4) (x² – 9) = 0
(x + 2i) (x – 2i) (x + 3) (x – 3)= 0
Since the solutions are 2i, -21, 3, and -3, and only real solutions to the equation are x-intercepts of the graph, the x-intercepts are 3 and – 3.

Question 6.
Find the solutions to 2x⁴ – 24x² + 40 = 0 and the x-intercepts of the graph of y = 2x⁴ – 24x² + 40.
Answer:
2(x⁴ – 12x² + 20) = 0
2(x² – 10) (x² – 2) = 0
Since all of the solutions √10, – √10, √2, and -√2 are real numbers, the x-intercepts of the graph are
√10, -√10, √2, and -√2.

Question 7.
Find the solutions to x⁴ – 64 = 0 and the x-intercepts of the graph of y = x⁴ – 64.
Answer:
(x² + 8) (x² – 8) = 0
(x + √8i) (x – √8i) (x + √8) (x – √8) = 0
The x-intercepts are 2√2 and – 2√2.

Question 8.
Use the fact that x⁴ + 64 = (x² – 4x + 8) (x² + 4x + 8) to explain how you know that the graph of y = x⁴ + 64 has no x-intercepts. You need not find the solutions.
Answer:
The x-intercepts of y = x⁴ + 64 are solutions to (x² – 4x + 8) (x² + 4x + 8) = 0. Both x² – 4x + 8 = 0 and x² + 4x + 8 = 0 have negative discriminant values of -16, so the equations x² – 4x + 8 = 0 and x² + 4x + 8 = 0 have no real solutions. Thus, the equation x⁴ + 64 = 0 has no real solutions, and the graph of y = x⁴ + 64 has no x-intercepts.

Since x⁴ + 64 = 0 has no real solutions, the graph of y = x⁴ + 64 has no x-intercepts.

Eureka Math Algebra 2 Module 1 Lesson 39 Exit Ticket Answer Key

Question 1.
Solve the quadratic equation x² + 9 = 0. What are the x-lntercepts of the graph of the function f(x) = x² + 9?
Answer:
x² + 9 = 0
x = √-9 or x = -√-9
x = 3√-1 or x = – 3√-1
x = 3i or x = – 3i
The x-intercepts of the graph of the function f(x) = x² + 9 are the real solutions to the equation x² + 9 = 0.
However, since both solutions to x² + 9 = 0 are not real, the function f(x) = x² + 9 does not have any x intercepts.

Question 2.
Find the solutions to 2x⁵ – 5x³ – 3x = 0. What are the x-intercepts of the graph of the function f(x) = 2x⁵ – 5x³ – 3x?
Answer:
(2x⁴ – 5x² – 3
x(x² – 3) (2x² + 1) = 0
x(x + √3) (x – √3) (2x² + 1) = 0
x(x + √3) (x – √3) (x + \(\frac{i \sqrt{2}}{2}\)) (x – \(\frac{i \sqrt{2}}{2}\)) = 0
Thus, x = 0, x = -√3, x = √3, x = –\(\frac{i \sqrt{2}}{2}\), or x = \(\frac{i \sqrt{2}}{2}\)
The solution are, 0, √3, -√3, \(\frac{i \sqrt{2}}{2}\) and –\(\frac{i \sqrt{2}}{2}\)
The x – intercepts of the graph of the function f(x) = 2x⁵ – 5x³ – 3x are the real solutions to the equation 2x⁵ – 5x³ – 3x = 0, so the x-intercepts are 0, √3, and -√3.