Eureka Math Algebra 2 Module 2 Lesson 7 Answer Key

Engage NY Eureka Math Algebra 2 Module 2 Lesson 7 Answer Key

Eureka Math Algebra 2 Module 2 Lesson 7 Example Answer Key

Example 1.
Use similar triangles to find the value of sec(θ°) in terms of one other trigonometric function.
Answer:

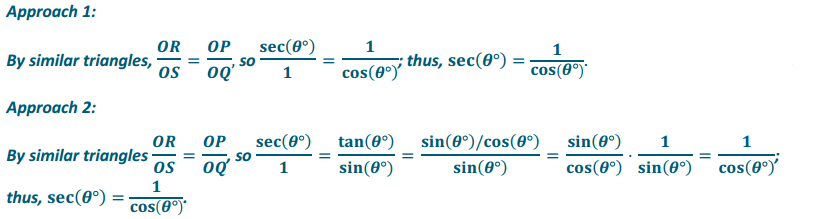
Example 2.

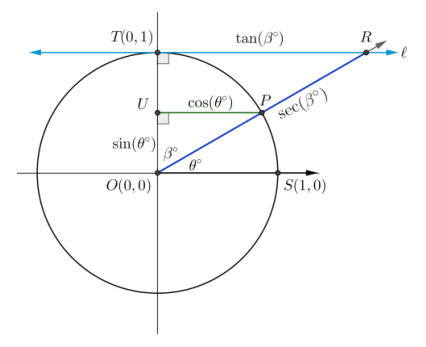
The horizontal blue line is tangent to the circle at (0, 1).

a. If two angles are complements with measures β and θ as shown in the diagram, use similar triangles to show that sec(β°) = \(\frac{1}{\sin \left(\theta^{\circ}\right)}\)
Answer:

b. If two angles are complements with measures β and θ as shown in the diagram, use similar triangles to show that tan(β°) = \(\frac{1}{\tan \left(\theta^{\circ}\right)}\)
Answer:

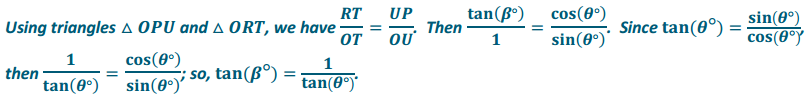
Eureka Math Algebra 2 Module 2 Lesson 7 Opening Exercise Answer Key

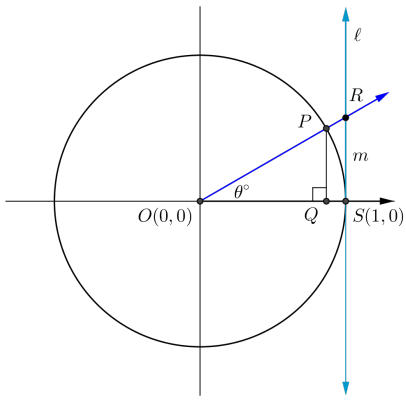
Find the length of each segment below in terms of the value of a trigonometric function.
OQ = _______ PQ = ________ RS = _______

Answer:
Debrief this exercise with a short discussion. For the purposes of this section, limit the values of θ to be between 0 and 90. Make sure that each student has labeled the proper line segments on his paper as sin(θ°), cos(θ°), tan(θ°), and sec(θ°) before moving on to Example 1.
→ Why is PQ = sin(θ°)? Why is OQ = cos(θ°)?
The values of the sine and cosine functions correspond to the y- and x-coordinates of a point on the unit circle where the terminal ray intersects the circle after a rotation of θ degrees about the origin.

→ Why is RS = tan(θ°)?
In Lesson 5, we used similar triangles to show that \(\overline{R S}\) had length \(\frac{P Q}{O Q}=\frac{\sin \left(\theta^{\circ}\right)}{\cos \left(\theta^{\circ}\right)}\).
This quotient is tan(θ°).

Since there are ways to calculate lengths for nearly every line segment in this diagram using the length of the radius, or the cosine, sine, or tangent functions, it makes sense to find the length of \(\overline{O R}\), the line segment on the terminal ray that intersects the
tangent line.

→ What do you call a line that intersects a circle at more than one point?
It is called a secant line.

→ In Lesson 6, we saw that RS = tan(θ°), where \(\overline{R S}\) lies on the line tangent to the unit circle at (1, 0), which helped to explain how this trigonometric function got its name. Let’s introduce a new function sec(θ°), the secant of θ, to be the length of \(\overline{O R}\) since this segment is on the secant line that contains the terminal ray. Then the secant of 6 is sec(θ°) = OR.

Eureka Math Algebra 2 Module 2 Lesson 7 Exercise Answer Key

Exercise 1.
The definition of the secant function is offered below. Answer the questions to better understand this definition and the domain and range of this function. Be prepared to discuss your responses with others in your class.

Let θ be any real number. In the Cartesian plane, rotate the nonnegative x-axis by θ degrees about the origin. Intersect this new ray with the unit circle to get a point (x_θ, y_θ).
If x_θ ≠ 0, then the value of sec(θ°) is \(\frac{1}{x_{\theta}}\). Otherwise, sec(θ°) is undefined.
In terms of the cosine function, sec(θ°) = \(\frac{1}{\cos \left(\theta^{\circ}\right)}\) for cos(θ°) ≠ 0.

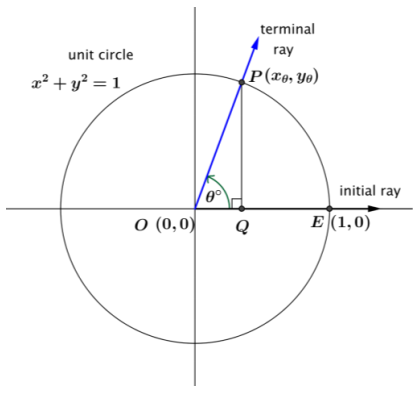
a. What is the domain of the secant function?
Answer:
The domain of the secant function is all real numbers θ such that θ ≠ 90 + 180k, for all integers k.

b. The domains of the secant and tangent functions are the same. Why?
Answer:
Both the tangent and secant functions can be written as rational expressions with cos(θ°) in the
denominator. That is, tan(θ°) = \(\frac{\sin \left(\theta^{\circ}\right)}{\cos \left(\theta^{\circ}\right)}\) and sec(θ°) = \(\frac{1}{\cos \left(\theta^{\circ}\right)}\). Since the restricted values in their domains occur when the denominator is zero, it makes sense that they have the same domain.

c. What is the range of the secant function? How is this range related to the range of the cosine function?
Answer:
Since sec(θ°) = \(\frac{1}{\cos \left(\theta^{\circ}\right)}\) and – 1 ≤ cos(θ°) ≤ 1, we see that either sec(θ°) ≥ 1, or sec(θ°) ≤ – 1. Thus, the range of the secant function is (- ∞, – 1] ∪ [1, ∞).

d. Is the secant function a periodic function? If so, what is its period?
Answer:
Yes, its period is 360.

Exercise 2.
In the diagram, the horizontal blue line is tangent to the unit circle at (0, 1).

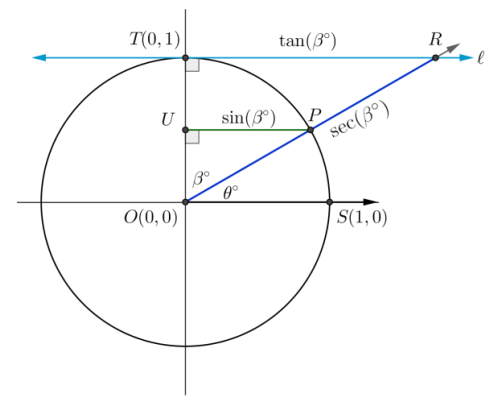
a. How does this diagram compare to the one given in the Opening Exercise?
Answer:
It is basically the same diagram with different angles and lengths marked. We can
consider a rotation through β degrees measured clockwise from the y-axis instead of a rotation through θ degrees measured counterclockwise from the x-axis. It is essentially a reflection of the diagram from the Opening Exercise across the diagonal line with equation y = x.

b. What is the relationship between β and θ?
Answer:
Angles TOP and SOP are complements, so β + θ = 90.

c. Which segment In the figure has length sin(θ°)? Which segment has length cos(θ°)?
Answer:
OU = sin(θ°), and UP = cos(θ°).

d. Which segment in the figure has length sin(β°)? Which segment has length cos(β°)?
Answer:
UP = sin(β°), and OU = cos(θ°).

e. How can you write sin(θ°) and cos(θ°) In terms of the trigonometric functions of β?
Answer:
sin(θ°) = cos(β°), and cos(θ°) = sin(β°).

Eureka Math Algebra 2 Module 2 Lesson 7 Problem Set Answer Key

Question 1.
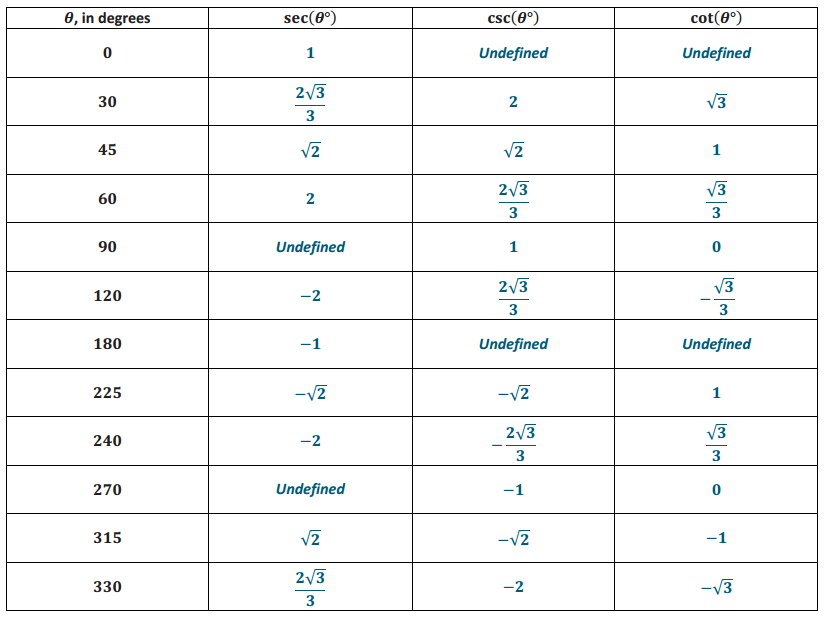
Use the reciprocal interpretations of sec(θ°), csc(θ°), and cot(θ°) and the unit circle provided to complete the table.


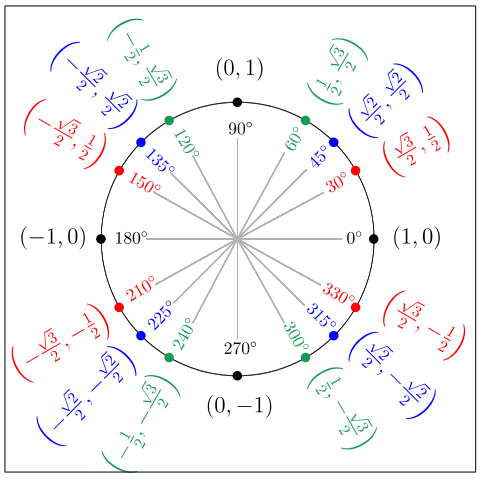
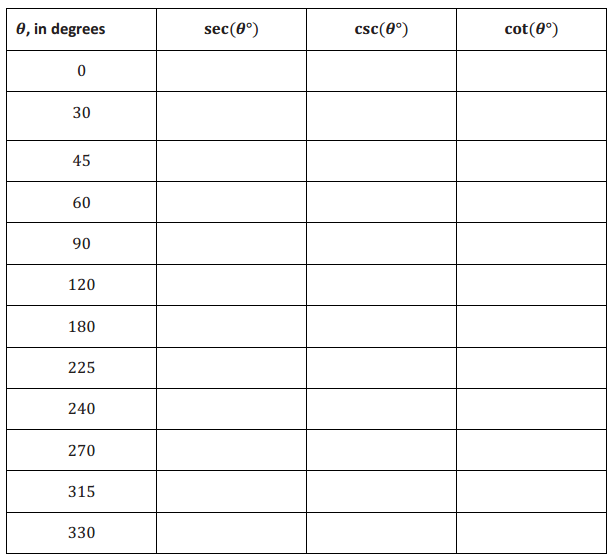
Answer:

Question 2.
Find the following values from the information given.
a. sec(θ°);           cos(θ°) = 0.3
b. csc(θ°);           sin(θ°) = – 0.05
c. cot(θ°);           tan(θ°) = 1000
d. sec(θ°);           cos(θ°) = – 0.9
e. csc(θ°);           sin(θ°) = 0
f. cot(θ°);            tan(θ°) = – 0.0005
Answer:

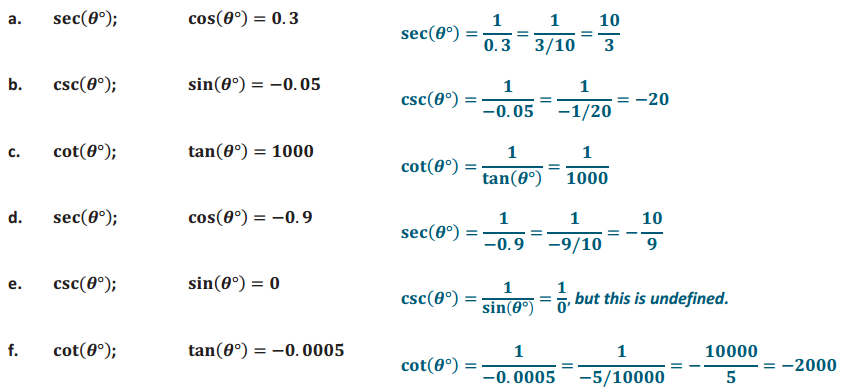
Question 3.
Choose three θ values from the table In Problem 1 for which sec(θ°), csc(θ°), and tan(θ°) are defined and not zero. Show that for these values of θ, \(\frac{\sec \left(\theta^{\circ}\right)}{\csc \left(\theta^{\circ}\right)}\) = tan(θ°).
Answer:

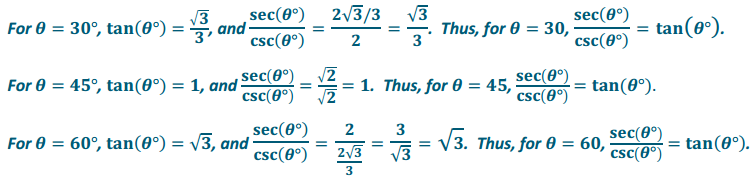
Question 4.
Find the value of sec(θ°) cos(θ°) for the following values of θ.
a. θ = 120
Answer:
We know that cos(120°) = –\(\frac{1}{2}\) so sec(120°) = – 2, and then sec(120°)cos(120°) = 1.

b. θ = 225
Answer:
We know that cos(225°) = –\(\frac{\sqrt{2}}{2}\), so sec(225°) = -√2, and then sec(225°)cos(225°) = 1.

c. θ = 330
Answer:
We know that cos(330°) = \(\frac{\sqrt{3}}{2}\), so sec(330°) = \(\frac{2}{\sqrt{3}}\), and then sec(330°)cos(330°) = 1.

d. Explain the reasons for the pattern you see in your responses to parts (a)-(c).
Answer:
If cos(θ°) ≠ 0, then sec(θ°) = \(\frac{1}{\cos \left(\theta^{\circ}\right)}\) so we know that sec(θ°) cos(θ°) = \(\frac{1}{\cos \left(\theta^{\circ}\right)}\) ∙ cos(θ°) = 1.

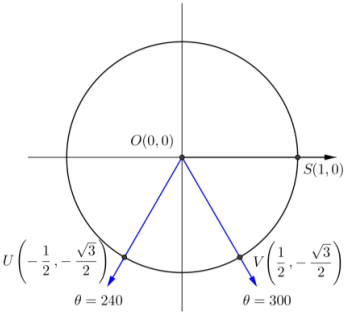
Question 5.
Draw a diagram representing the two values of θ between 0 and 360 so that sin(θ°) = –\(\frac{\sqrt{3}}{2}\) . Find the values tan(θ°), sec(θ°), and csc(θ°) for each value of θ.
Answer:
tan(240°) = √3 sec(240°) = – 2, and csc(240°) = –\(\frac{2 \sqrt{3}}{3}\).
tan(300°) = -√3 sec(300°) = 2, and csc(300°) = –\(\frac{2 \sqrt{3}}{3}\)

Question 6.
Find the value of (sec(θ°))² – (tan(θ°))² when θ = 225.
Answer:
(sec(225°))² – (tan(225°))² = (√2)² – 1² = 1

Question 7.
Find the value of (csc(θ°))² – (cot(θ°))² when θ = 330.
Answer:
(csc(θ))² – (cot(θ°))² = (-2)² – (-√3)² = 4 – 3 = 1

Extension:

Question 8.
Using the formulas sec(θ°) = \(\frac{1}{\cos \left(\theta^{\circ}\right)}\), csc (θ°) = \(\frac{1}{\sin \left(\theta^{\circ}\right)}\) = and cot(θ°) = \(\frac{1}{\tan \left(\theta^{\circ}\right)}\) show that \(\frac{\sec \left(\theta^{\circ}\right)}{\csc \left(\theta^{\circ}\right)}\) = tan (θ°),
where these functions are defined and not zero.
Answer:

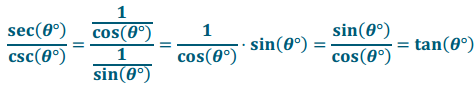
Question 9.
Tara showed that \(\frac{\sec \left(\theta^{\circ}\right)}{\csc \left(\theta^{\circ}\right)}\) = tan(θ°), for values of θ for which the functions are defined and csc(θ°) ≠ 0, and then concluded that sec(θ°) = sin(θ°) and csc(θ°) = cos(θ°). Explain what is wrong with her reasoning.
Answer:
Just because \(\frac{A}{B}=\frac{C}{D}\), this does not mean that A = C and B = D. It only means that they are equivalent fractions. For instance, \(\frac{3}{4}=\frac{9}{12}\). Substituting any value of θ verifies that Tara is incorrect. Also, since the only values of θ in the range of both secant and sine are -1 and 1, we would have either sec(θ°) = sin(θ°) = – 1 or sec(θ°) = sin (θ°) = 1. Since the value of the sine function is either -1 or 1, the value of the cosine function would be zero. Since sec(θ°) = \(\frac{1}{\cos \left(\theta^{\circ}\right)}\) we would have cos(θ°) = 1 or cos(θ°) = – 1. Since cos(θ°) cannot be simultaneously zero and nonzero, it Is 1m possible to have sec(θ°) = sin(θ°) and csc(θ°) = cos(θ°).

Eureka Math Algebra 2 Module 2 Lesson 7 Exit Ticket Answer Key

Consider the following diagram, where segment AB is tangent to the circle at D. Right triangles BAO, BOD, OAD, and ODC are similar. Identify each length AD, OA, OB, and BD as one of the following: tan(θ°), cot(θ°), sec(θ°), and csc(θ°).

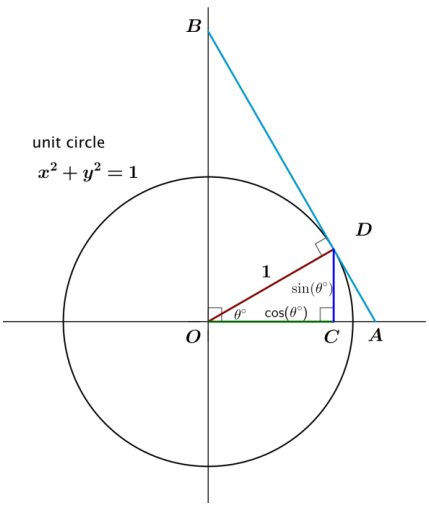
Answer:

Eureka Math Algebra 2 Module 2 Lesson 7 Discussion Answer Key

Definitions of the cosecant and cotangent functions are offered below. Answer the questions to better understand the definitions and the domains and ranges of these functions. Be prepared to discuss your responses with others in your class.

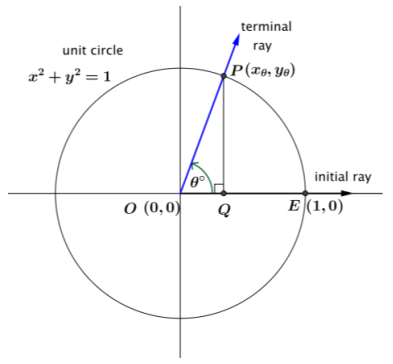
Let θ be any real number such that θ ≠ 180k, for all integers k. In the Cartesian plane, rotate the initial ray by θ degrees about the origin. Intersect the resulting terminal ray with the unit circle to get a point (x_θ, y_θ).
The value of csc(θ°) is \(\frac{1}{y_{\theta}}\).
The value of cot(θ°) is \(\frac{x_{\theta}}{y_{\theta}}\).

The secant, cosecant, and cotangent functions are often
referred to as reciprocal functions. Why do you think these functions are so named?
Answer:
These functions are the reciprocals of the three main trigonometric functions:
sec (θ°) = \(\frac{1}{\cos \left(\theta^{\circ}\right)}\) csc (θ°) = \(\frac{1}{\sin \left(\theta^{\circ}\right)}\), and cot (θ°) = \(\frac{1}{\tan \left(\theta^{\circ}\right)}\).

Why are the domains of these functions restricted?
Answer:
We restrict the domain to prevent division by zero.
We restrict the domain because the geometric shapes defining the functions must make sense (i.e., based on the intersection of distinct parallel lines).

The domains of the cosecant and cotangent functions are the same. Why?
Answer:
Both the cosecant and cotangent functions are equal to rational expressions that have sin(θ°) in the denominator.

What is the range of the cosecant function? How is this range related to the range of the sine function?
Answer:
The sine function has range [- 1, 1], so the cosecant function has range (- ∞, – 1] ∪ [1, ∞). The two ranges only intersect at – 1 and at 1.

What is the range of the cotangent function? How ¡s this range related to the range of the tangent function?
Answer:
The range of the cotangent function is all real numbers. This is the some as the range of the tangent function.