Engage NY Eureka Math Algebra 2 Module 1 End of Module Assessment Answer Key
Eureka Math Algebra 2 Module 1 End of Module Assessment Answer Key
Question 1.
A parabola is defined as the set of points in the plane that are equidistant from a fixed point (called the focus of the parabola) and a fixed line (called the directrix of the parabola).
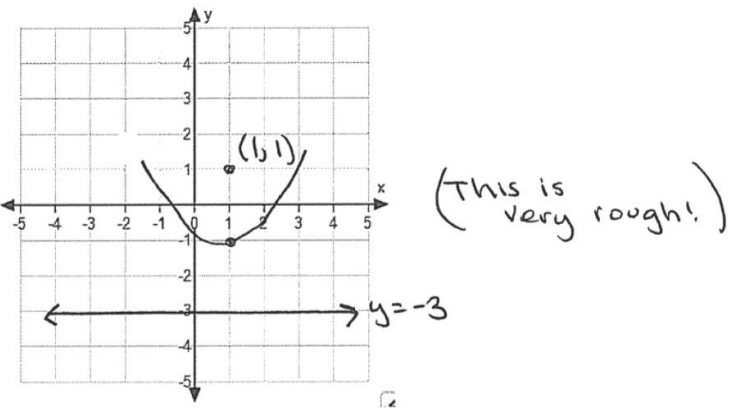
Consider the parabola with focus point (1, 1) and directrix the horizontal line y = – 3.
a. What are the coordinates of the vertex of the parabola?
Answer:
(1, – 1)
b. Plot the focus and draw the directrix on the graph below. Then draw a rough sketch of the parabola.
Answer:
c. Find the equation of the parabola with this focus and directrix.
Answer:
A point (x, y) on the parabola is equidistant from the directrix and the focus:
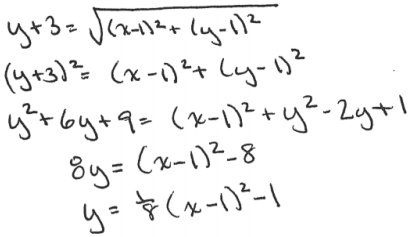
d. What is the y-intercept of this parabola?
Answer:
At the y-intercept x = 0, so y = \(\frac{1}{8}\)(-1)2 – 1 = \(\frac{-7}{8}\)
\(\frac{-7}{8}\) is the y intercept.
e. Demonstrate that your answer from part (d) is correct by showing that the y-intercept you identified is indeed equidistant from the focus and the directrix.
Answer:
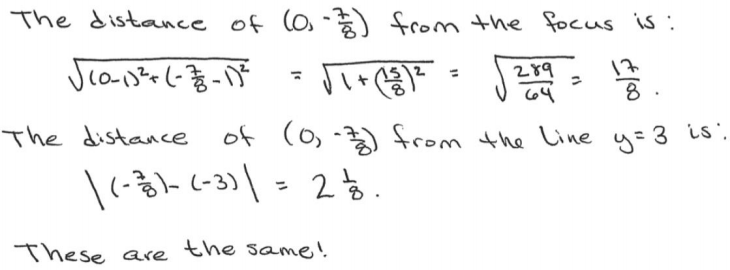
f. Is the parabola in this question (with focus point (1, 1) and directrix y = – 3) congruent to a parabola with focus (2, 3) and directrix y = – 1? Explain.
Answer:

g. Is the parabola in this question (with focus point (1, 1) and directrix y = – 3) congruent to the parabola with equation given by y = x2? Explain.
Answer:
No, y = x2 and y = \(\frac{1}{8}\)(x – 1)2 + 1 do not have the same leading coefficient so they are not congruent. (y = x2 has a leading coefficient 1, and y = \(\frac{1}{8}\)(x – 1)2 + 1 had a leading coefficient \(\frac{1}{8}\).
h. Are the two parabolas from part (g) similar? Why or why not?
Answer:
Yes! Because all parabolas are similar.
Question 2.
The graph of the polynomial function f(x) = x3 + 4x2 + 6x + 4 is shown below.
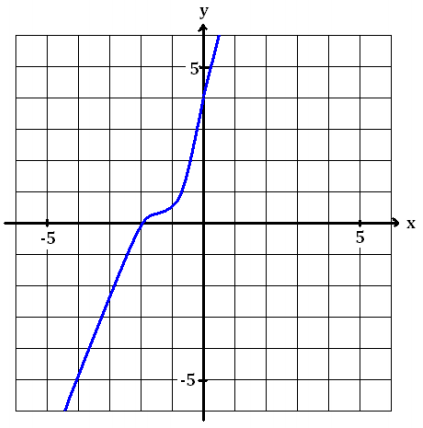
a. Based on the appearance of the graph, what does the real solution to the equation x3 + 4x2 + 6x + 4 = 0 appear to be? Jiju does not trust the accuracy of the graph. Prove to her algebraically that your answer is in fact a zero of y = f(x).
Answer:
The real zero appears to be x = -2.
f(-2) = (-2)3 + 4(-2)2 + 6(-2) + 4
= – 8 + 16 – 12 + 4
= 0
b. Write f as a product of a linear factor and a quadratic factor, each with real number coefficients.
Answer:
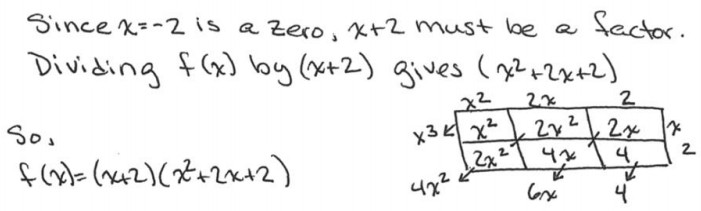
c. What is the value of f(10)? Explain how knowing the linear factor of f establishes that f(10) is a multiple of 12.
Answer:
f(10) = (10 + 2) (100 + 20 + 2)
= 12 (122)
= 1220 + 244
= 1464
f(10) is a multiple of 12 because f(x) has a linear factor of x + 2, and x + 2 = 12, when x = 10.
d. Find the two complex number zeros of y = f(x).
Answer:
We need to solve x2 + 2x + 2 = 0
x2 + 2x + 1 = – 1
(x + 1)2 = – 1
x + 1 = ± 1
x = – 1 ± l
e. Write f as a product of three linear factors.
Answer:
f(x) = (x + 2) (x – ( – 1 + l)) (x – (- 1 – l)
Question 3.
A line passes through the points (- 1, 0) and P = (0, t) for some real number t and intersects the circle x2 + y2 = 1 at a point Q different from (- 1, 0).
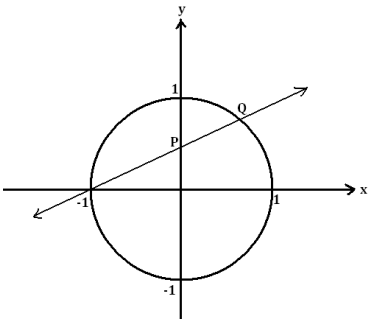
a. If t = \(\frac{1}{2}\), so that the point P has coordinates (o, \(\frac{1}{2}\)), find the coordinates of the point Q.
Answer:
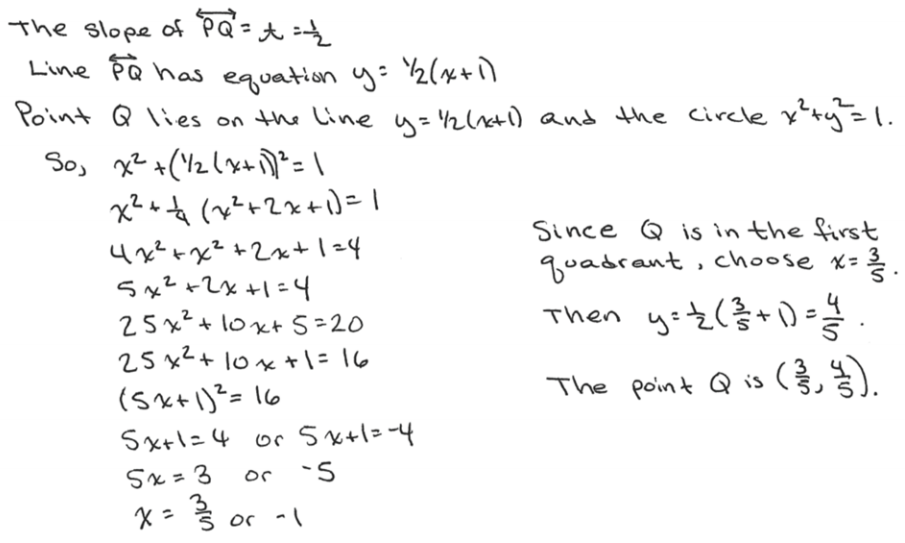
A Pythagorean triple is a set of three positive integers a, b, and c satisfying a2 + b2 = c2. For example, setting a = 3, b = 4, and c = 5 gives a Pythagorean triple.
b. Suppose that \(\left(\frac{a}{c}, \frac{b}{c}\right)\) is a point with rational number coordinates lying on the circle x2 + y2 = 1. Explain why then a, b, and c form a Pythagorean triple.
Answer:
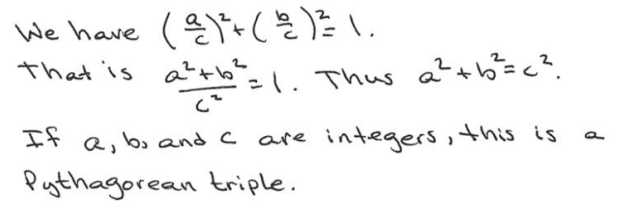
c. Which Pythagorean triple is associated with the point Q = \(\left(\frac{5}{13}, \frac{12}{13}\right)\) on the circle?
Answer:
5, 12, 13
d. If Q = \(\left(\frac{5}{13}, \frac{12}{13}\right)\) what is the value of t so that the point P has coordinates (0, t)?
Answer:
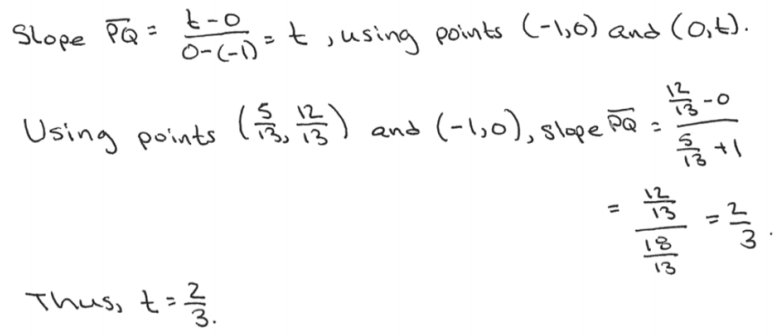
e. Suppose we set x = \(\frac{1-t^{2}}{1+t^{2}}\) and y = \(\frac{2 t}{1+t^{2}}\) for a real number t. Show that (x, y) is then a point on the circle x2 + y2 = 1.
Answer:
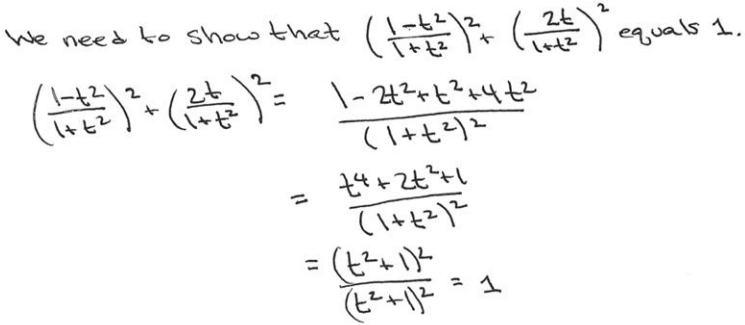
f. Set t = \(\frac{3}{4}\) in the formulas x = \(\frac{1-t^{2}}{1+t^{2}}\) and y = \(\frac{2 t}{1+t^{2}}\). Which point on the circle x2 + y2 = 1 does this give? What is the associated Pythagorean triple?
Answer:
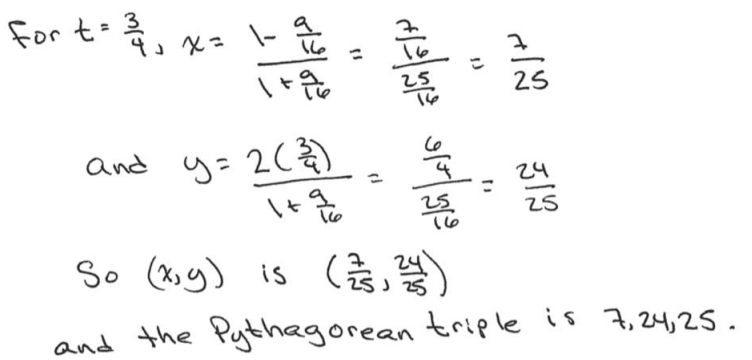
g. Suppose t is a value greater than 1, P = (0, t), and Q is the point in the second quadrant (different from (- 1,0)) at which the line through (- 1,0) and P intersects the circle x2 + y2 = 1. Find the coordinates of the point Q in terms of t.
Answer:

Question 4.
a. Write a system of two equations in two variables where one equation is quadratic and the other is linear such that the system has no solution. Explain, using graphs, algebra, and/or words, why the system has no solution.
Answer:
y = x2
y = – 1
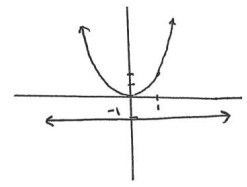
From the graph, these two curves do not intersect, and so there is no solution to this system of equations.
b. Prove that x = \(\sqrt{-5 x-6}\) has no solution.
Answer:
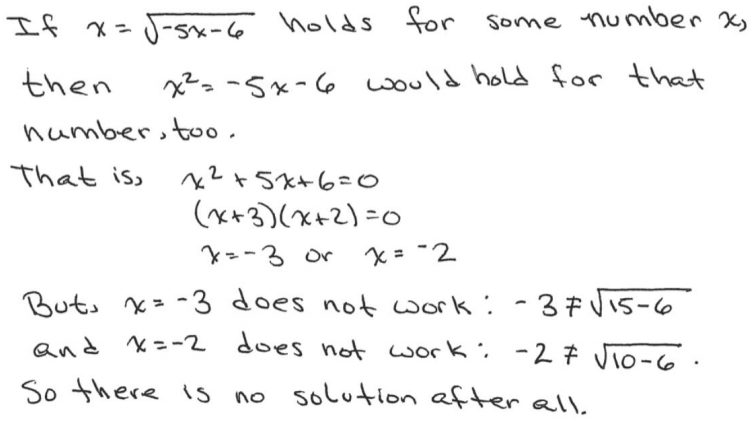
c. Does the following system of equations have a solution? If so, find one. If not, explain why not.
2x + y + z = 4
x – y + 3z = – 2
– x + y + z = – 2
Answer:
2x + y + z = 4 → 1
x – y + 3z = – 2 → 2
– x + y + z = – 2 → 3
