Engage NY Eureka Math Algebra 2 Module 1 Lesson 2 Answer Key
Eureka Math Algebra 2 Module 1 Lesson 2 Example Answer Key
Example 1.
Use the tabular method to multiply (x + 8)(x + 7) and combine like terms.
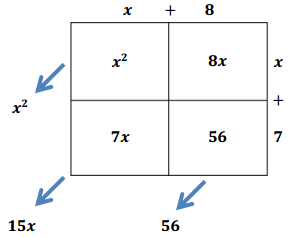
Answer:
(x + 8) (x + 7) = x2 + 15x + 56
→ Explain how the result x2 + 15 + 56 is related to 756 determined in the Opening Exercise.
If 𝐠is replaced with 20 in x2 + 15x + 56, then the calculation becomes the same as the one shown in the Opening Exercise: (20) 2 + 15(20) + 56 = 400 + 300 + 56 = 756.
→ How can we multiply these binomials without using a table?
Think of x + 8 as a single number and distribute over x + 7:
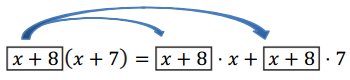
Next, distribute the x over x + 8 and the 7 over x + 8. Combining like terms shows that
(x + 8)(x + 7) =x2 + 15x + 56.
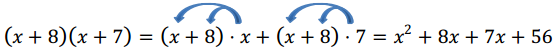
Example 2.
Multiply the polynomials (x – 1)(x4 + x3 + x2 + x + 1) using a table. Generalize the pattern that emerges by writing down an identity for (x – 1)(xn + xn-1 + ….. + x2 + x + 1) for n a positive integer.
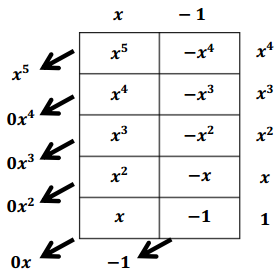
Answer:
(x – 1) (x4 + x3 + x2 + x + 1) = x5 – 1
The pattern suggests (x – 1) (xn + xn-1 + …….. + x2 + x + 1) = xn+1 – 1.
Eureka Math Algebra 2 Module 1 Lesson 2 Opening Exercise Answer Key
Show that 28 × 28 = (20 + 8)(20 + 7) using an area model. What do the numbers you placed inside the four rectangular regions you drew represent?
Answer:
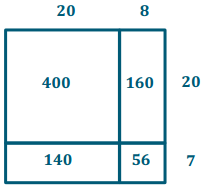
28 × 27 = (20 + 8)(20 + 7)
= 400 + 140 + 160 + 56
= 756
The numbers placed into the blanks represent the number of unit squares (or square units) in each sub-rectangle.
Eureka Math Algebra 2 Module 1 Lesson 2 Exercise Answer Key
Exercise 1.
Use the tabular method to multiply (x2 + 3x + 1) (x2 – 5x + 2) and combine like terms.
Answer:
Sample student work:
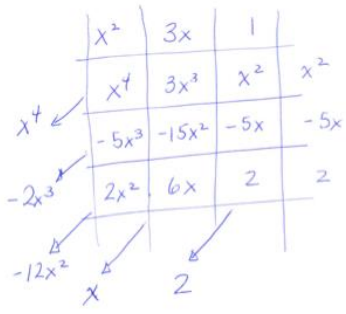
(x2 + 3x + 1) (x2 – 5x + 2) = x4 – 2x3 – 12x2 + x + 2
Exercise 2.
Use the tabular method to multiply (x2 + 3x + 1) (x2 – 2) and combine like terms.
Answer:
Sample student work:
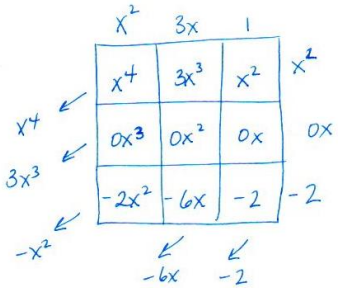
(x2 + 3x + 1)(x2 – 2) = x4 + 3x3 – x2 – 6x – 2
Another solution method would be to omit the row for 0x in the table and to manually add all table entries instead of adding along the diagonals:
(x2 + 3x + 1)(x2 – 2) = x4 + 3x3 + x2 – 2x2 – 6x – 2
= x4 + 3x3 – x2 – 6x – 2
Exercise 3.
Multiply (x – y) (x3 + x2y + xy2 + y3) using the distributive property and combine like terms. How is this calculation similar to Example 2?
Answer:
Distribute the expression x3 + x2y + xy2 + y3 through x – y to get
(x – y) (x3 + x2y + xy2 + y3) = x4 + x3y + x2y2 + xy3 – x3y – x2y2 – xy3 – y4 = x4 – y4
Substitute 1 in for 𝐠to get the identity for n = 3 in Example 2.
This calculation is similar to Example 2 because it has the same structure. Substituting 1 for y results in the same expression as Example 2.
Exercise 4.
Multiply (x2 – y2) (x2 + y2) using the distributive property and combine like terms. Generalize the pattern that emerges to write down an identity for (xn – yn) (xn + yn) for positive integers n.
Answer:
(x2 – y2) (x2 + y2) = (x2 – y2) ∙ x2 + (x2 – y2) ∙ y2 = x4 – x2y2 + x2y2 – y4 = x4 – y4.
Generalization: (xn – yn) (xn + yn) = x2n – y2n.
Sample student work:
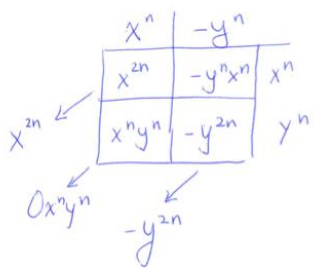
(xn – yn) (xn + yn) = x2n – y2n
→ The generalized identity x2n – y2n = (xn – yn) (xn + yn) is used several times in this module. For example, it helps to recognize that 2130 – 1 is not a prime number because it can be written as (265 – 1)(265 + 1). Some of the problems in the Problem Set rely on this type of thinking.
Eureka Math Algebra 2 Module 1 Lesson 2 Problem Set Answer Key
Question 1.
Complete the following statements by filling in the blanks.
a. (a + b) (c + d + e) = ac + ad + ae + ______ + ______ + ________
Answer:
bc, bd, be
b. (r – s)2 = ( ______ )2 – ( ______ )rs + s2
Answer:
r,2
C. (2x + 3y)2 = (2x)2 + 2(2x)(3y) + ( _______ )2
Answer:
3y
d. (w – 1) (1 + w + w2) = ______ – 1
Answer:
W3
e. a2 – 16 = (a + ______)(a – ______)
Answer:
44
f. (2x + 5y)(2x – 5y) = ______ – ______
Answer:
4x2, 25y2
g. (221 – 1)(221 + 1) = ______ – 1
Answer:
242
h. [(x – y) – 3] [(x – y) + 3] = ( ______ )2 – 9
Answer:
x – y
Question 2.
Use the tabular method to multiply and combine like terms.
a. (x2 – 4x + 4) (x + 3)
Answer:
Sample student work:
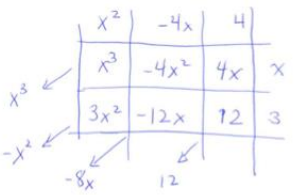
(x2 – 4x + 4) (x + 3) = x3 – x2 – 8x + 12
b. (11 – 15x – 7x2) (25 – 16x2)
Answer:
Sample student work:
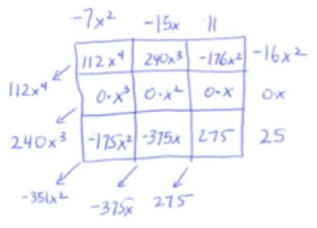
(11 – 15x – 7x2) (25 – 16x2) = 112x4 + 240x3 – 315x2 – 375x + 275
c. (3m3 + m2 – 2m – 5) (m2 – 5m – 6)
Answer:
Sample student work:
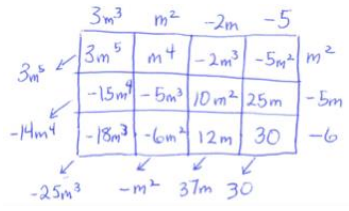
(3m3 + m2 – 2m – 5) (m2 – 5m – 6) = 3m5 – 14m4 – 25m3 – m2 + 37m + 30
d. (x2 – 3x + 9) (x2 + 3x + 9)
Answer:
Sample student work:
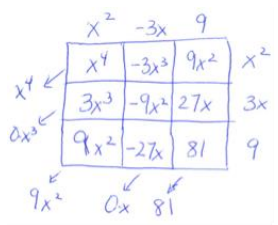
(x2 – 3x + 9) (x2 + 3x + 9) = x4 + 9x2 + 81
Question 3.
Multiply and combine like terms to write as the sum or difference of monomials.
a. 2a(5 + 4a)
Answer:
8a2 + 10a
b. x3(x + 6) + 9
Answer:
x4 + 6x3 + 9
c. \(\frac{1}{8}\)(96z + 24z2)
Answer:
12z + 3z2
d. 223(284 – 281)
Answer:
2107 – 2104
e. (x – 4)(x + 5)
Answer:
x2 + x – 20
f. (10w – 1) (10w + 1)
Answer:
100w2 – 1
g. (3z2 – 8) (3z2 + 8)
Answer:
9z4 – 64
h. (- 5w – 3)w2
Answer:
– 5w3 – 3w2
i. 8y1000 (y12200 + 0. 125y)
Answer:
8y13200 + y1001
j. (2r + 1)(2r2 + 1)
Answer:
4r3 + 2r2 + 2r + 1
k. (t – 1)(t + 1)(t2+ 1)
Answer:
t4 – 1
l. (w – 1)(w5 + w4 + w3 + w2 + w + 1)
Answer:
w6 – 1
m. (x + 2) (x + 2) (x + 2)
Answer:
x3 + 6x2 + 12x + 8
n. n(n + 1)(n + 2)
Answer:
n3 + 3n2 + 2n
o. n(n + 1)(n + 2)(n + 3)
Answer:
n4 + 6n3 + 11n2 + 6n
p. n(n + 1) (n + 2) (n + 3) (n + 4)
Answer:
n5 + 10n4 + 35n3 + 50n2 + 24n
q. (x + 1)(x3 – x2+ x – 1)
Answer:
x4 – 1
r. (x + 1)(x5 – x4 + x3 – x2 + x – 1)
Answer:
x6 – 1
s. (x + 1)(x7 – x6 + x5 – x4 + x3 – x2 + x – 1)
Answer:
x8 – 1
t. (m3 – 2m + 1) (m2 – m + 2)
Answer:
m5 – m4 + 3m2 – 5m + 2
Question 4.
Polynomial expressions can be thought of as a generalization of place value.
a. Multiply 214 × 112 using the standard paper-and-pencil algorithm.
Answer:
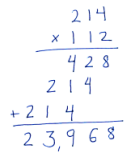
b. Multiply (2x2 + x + 4) (x2 + x + 2) using the tabular method and combine like terms.
Answer:
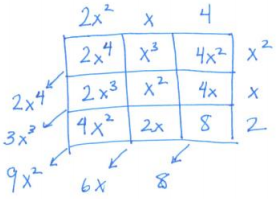
(2x2 + x + 4) (x2 + x + 2) = 2x4 + 3x3 + 9x2 + 6x + 8
c. Substitute x = 10 into your answer from part (b).
Answer:
23,968
d. Is the answer to part (c) equal to the answer from part (a)? Compare the digits you computed in the
algorithm to the coefficients of the entries you computed in the table. How do the place-value units of the digits compare to the powers of the variables in the entries?
Answer:
Yes. The digits computed in the algorithm are the same as the coefficients computed in the table entries. The zero-degree term in the table corresponds to the ones unit, the first-degree terms in the table correspond to the tens unit, the second-degree terms in the table correspond to the hundreds unit, and so on.
Question 5.
Jeremy says (x – 9)(x7 + x6 + x5 + x4 + x3 + x2 + x + 1) must equal x7 + x6 + x5 + x4 + x3 + x2 + x + 1 because when x = 10, multiplying by x – 9 is the same as multiplying by 1.
a. Multiply (x – 9)(x7 + x6 + x5 + x4 + x3 + x2 + x + 1).
Answer:
x8 – 8x7 – 8x6 – 8x5 – 8x4 – 8x3 – 8x2 – 8x – 9
b. Substitute x = 10 into your answer.
Answer:
100000000 – 80000000 – 8000000 – 800000 – 80000 – 8000 – 800 – 80 – 9
100000000 – 88888889 = 11111111
c. Is the answer to part (b) the same as the value of x7 + x6 + x5 + x4 + x3 + x2 + x + 1 when x = 10?
Answer:
Yes
d. Was Jeremy right?
Answer:
No, just because it is true when x is 10 does not make it true for all real x The two expressions are not algebraically equivalent.
Question 6.
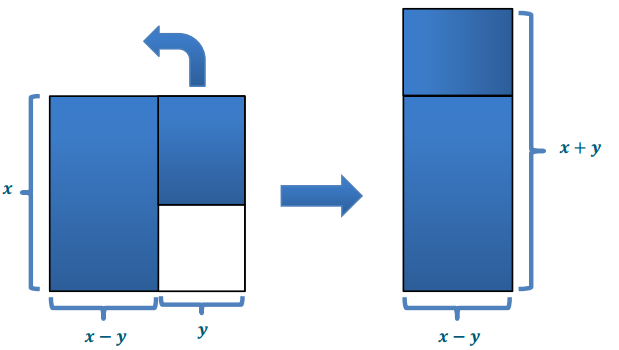
In the diagram, the side of the larger square is x units, and the side of the smaller square is y units. The area of the shaded region is (x2 – y2) square units. Show how the shaded area might be cut and rearranged to Illustrate that the area is (x – y)(x + y) square units.

Answer:
Eureka Math Algebra 2 Module 1 Lesson 2 Exit Ticket Answer Key
Multiply (x – 1) (x3 + 4x2 + 4x – 1) and combine like terms. Explain how you reached your answer.
Answer:
Tabular method:
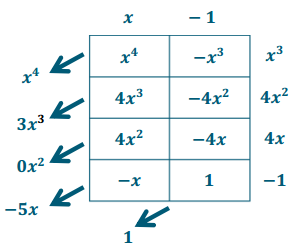
(x – 1) (x3 + 4x2 + 4x – 1) = x4 + 3x3 – 5x + 1
Using the distributive property (Each-With-Each):
(x – 1) (x3 + 4x2 + 4x – 1) = x4 + 4x3 + 4x2 – x – x3 – 4x2 – 4x + 1 = x4 + 3x3 – 5x + 1