Eureka Math Algebra 2 Module 1 Lesson 3 Answer Key

Engage NY Eureka Math Algebra 2 Module 1 Lesson 3 Answer Key

Eureka Math Algebra 2 Module 1 Lesson 3 Opening Exercise Answer Key

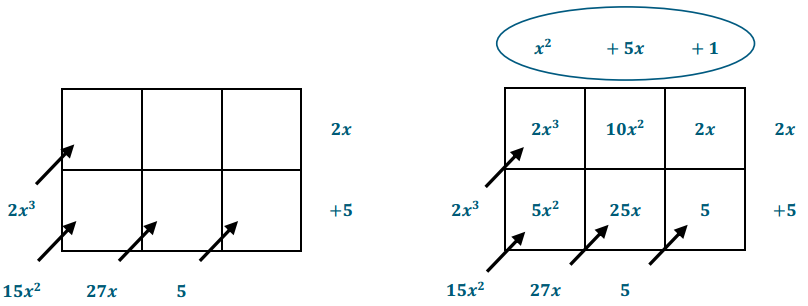
a. Multiply these polynomials using the tabular method.
(2x + 5) (x² + 5x + 1)
Answer:
The product is 2x³ + 15x² + 27x + 5

b. How can you use the expression in part (a) to quickly multiply 25 ∙ 151?
Answer:
If you let x = 10 then the product is
2(10)³ + 15(10)² + 27(10) + 5
= 2000 + 1500 + 270 + 5
= 3775.

Eureka Math Algebra 2 Module 1 Lesson 3 Problem Set Answer Key

Use the reverse tabular method to solve these division problems.

Question 1.
\(\frac{2 x^{3}+x^{2}-16 x+15}{2 x-3}\)
Answer:
x² + 2x – 5

Question 2.
\(\frac{\left(3 x^{5}+12 x^{4}+11 x^{3}+2 x^{2}-4 x-2\right)}{\left(3 x^{2}-1\right)}\)
Answer:
x³ + 4x² + 4x + 2

Question 3.
\(\frac{x^{3}-4 x^{2}+7 x-28}{x^{2}+7}\)
Answer:
x – 4

Question 4.
\(\frac{x^{4}-2 x^{3}-29 x-12}{x^{3}+2 x^{2}+8 x+3}\)
Answer:
x – 4

Question 5.
\(\frac{6 x^{5}+4 x^{4}-6 x^{3}+14 x^{2}-8}{6 x+4}\)
Answer:
x⁴ – x² + 3x – 2

Question 6.
\(\frac{\left(x^{3}-8\right)}{(x-2)}\)
Answer:
x² + 2x + 4

Question 7.
\(\frac{x^{3}+2 x^{2}+2 x+1}{x+1}\)
Answer:
x² + x + 1

Question 8.
\(\frac{x^{4}+2 x^{3}+2 x^{2}+2 x+1}{x+1}\)
Answer:
x³ + x² + x + 1

Question 9.
Use the results of Problems 7 and 8 to predict the quotient of \(\frac{x^{5}+2 x^{4}+2 x^{3}+2 x^{2}+2 x+1}{x+1}\).
Explain your prediction. Then check your prediction using the reverse tabular method.
Answer:
The quotient is x⁴ + x³ + x² + x + 1 In Problems 7 and 8, the result is a polynomial of degree one less than the dividend where all the coefficients were 1. The dividend in this problem has the same structure except it was degree 5 and it is also divided by x + 1.

Question 10.
Use the results of Problems 7 – 9 above to predict the quotient of \(\frac{x^{4}-2 x^{3}+2 x^{2}-2 x+1}{x-1}\). Explain your prediction. Then check your prediction using the reverse tabular method.
Answer:
The quotient is x³ – x² + x – 1.

Question 11.
Make and test a conjecture about the quotient of ??\(\frac{x^{6}+x^{5}+2 x^{4}+2 x^{3}+2 x^{2}+x+1}{x^{2}+1}\). Explain your reasoning.
Answer:
The quotient is x⁴ + x³ + x² + x + 1 Since we are missing the x term, there will not be two x⁵ or two x terms. Otherwise it will follow the same pattern as Problems 7 – 9.

Question 12.
Consider the following quotients:
\(\frac{4 x^{2}+8 x+3}{2 x+1}\) and \(\frac{483}{21}\)

a. How are these expressions related?
If we let x = 10 then 4x² + 8x + 3 = 4(10)² + 8(10) + 3 = 483 and 2x + 1 = 2(10) + 1 = 21, so
\(\frac{4 x^{2}+8 x+3}{2 x+1}=\frac{483}{21}\)

b. Find each quotient.
Answer:
\(\frac{4 x^{2}+8 x+3}{2 x+1}\) = 2x + 3 and \(\frac{483}{21}\) = 23

c. Explain the connection between the quotients.
Answer:
If we let x = 10 then. 2x + 3 = 2(10) + 3 = 23.

Eureka Math Algebra 2 Module 1 Lesson 3 Exit Ticket Answer Key

Question 1.
Find the quotient. Justify your answer.
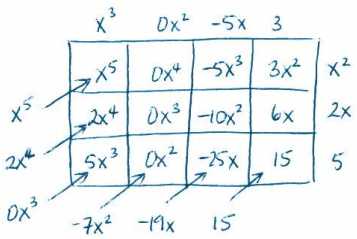
\(\frac{x^{5}+2 x^{4}-7 x^{2}-19 x+15}{x^{2}+2 x+5}\)
Answer:
The quotient is x³ – 5x + 3

Eureka Math Algebra 2 Module 1 Lesson 3 Exploratory Challenge Answer Key

Question 1.
Does \(\frac{2 x^{3}+15 x^{2}+27 x+5}{2 x+5}\) = (x² + 5x + 1) Justify your answer.

Answer:
The partially completed tables shown below provide some suggestions for scaffolding this lesson exploration (if needed). Encourage students to place the dividend where the product would result from multiplying and the quotient where one of the factors would be located. Then, have them work backward to show that the top row of this table is the quotient, x² + 5 + 1. Since the table is two by three, it would make sense that 2 + 5 is positioned along the vertical side on the right. Notice that the terms of the quotient are located around the left and bottom side of the table. This is where they would appear if these terms represented the result of multiplying two polynomials whose product was 2x³ + 15 + 27 + 5. Notice also that the divisor is positioned along the right side of the table (as was found with one of the factors in the earlier tabular method multiplication problems). The arrows in the diagram indicate that the diagonal entries must sum to the term outside the table (e.g., 15x² = 5x² + 10x²).

After students have had a few minutes to discuss their ideas in groups, lead a short discussion (as needed) if they appear to be stuck. Use these questions to prompt groups while also circulating around the room.

→ The quotient will be the polynomial that would go along the top of the table. Remember we know it should be x² + 5x + 1. How can you get started to confirm this using the dividend and the divisor?
→ We need to think about how the divisor terms fill back into the table, and then we need to use the
2x and the 5 terms to determine the other factor for each column at the top of the table.

→ Are there any cells in the table that we can fill in based on the information we have? What must be in the top left cell? Why?
→ The 2x³ term will be the top left entry, and the 5 will be the bottom right entry. Because the diagonals add to produce the terms of the product, we know that the top left and bottom right entries must be the first and last terms of the dividend since those terms do not involve combining any like terms when we compute the product.

→ What must the first term of the missing polynomial in the top row be?
→ It would have to be x² since that term and 2x must multiply to be 2x³.

→ What goes in the rest of the cells in the first column? How can you continue this pattern?
→ Multiply x² and 5 to get 5x². Then the 2^nd column in the first row would need to be 10x² because
15x² = 10x² + 5x². Since the 2^nd column of the first row is now known, we can figure out the remaining term of the quotient since that term times 2x would have to equal 10x².

→ Compare your work on this problem with the Opening Exercise. How could you verify that x² + 5x + 1 really is the quotient? Explain?
→ In the Opening Exercise, we multiplied the quotient and divisor and got the dividend.
So (2x + 5)(x² + 5x + 1) must equal 2x³ + 15x² + 27x + 5.

Question 2.
Describe the process you used to determine your answer to Exercise 1.
Answer:
Student descriptions will vary but should be similar to the detailed directions provided on the following page. Check each group’s work before moving on to the next exercise. Have a couple of groups present their solution methods to the Exercises 1 and 2 on the board, especially if other groups seem to be struggling. Then, if needed, go over the steps outlined below in detail to clarify this process for all students. Provide additional scaffolding if needed.

Step 1 – Draw a table with factors along the right sides and bottom corner, and fill in known entries along the top left and bottom right.

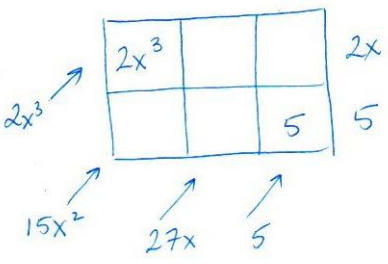
Step 2 – Use the top left entry to find the second-degree term along the top. It has to be x² because 2x ∙ x² = 2x³.

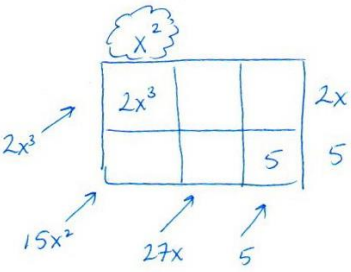
Step 3 – Use x² and 5 to find the bottom left entry, 5x², and then use that entry to find the top middle term. It has to be 10x² because 5x² + 10x² = 15x².

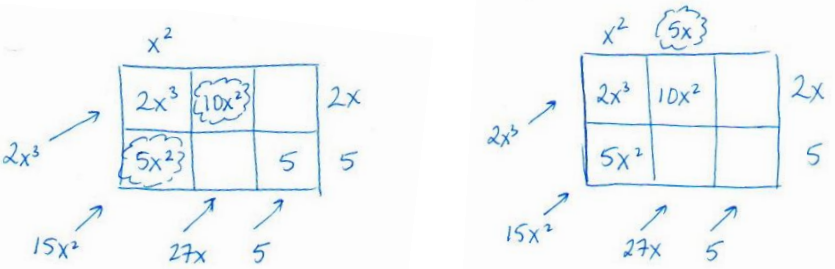
Step 4 – Repeat these steps to fill in the bottom entry in the 2^nd and last columns.

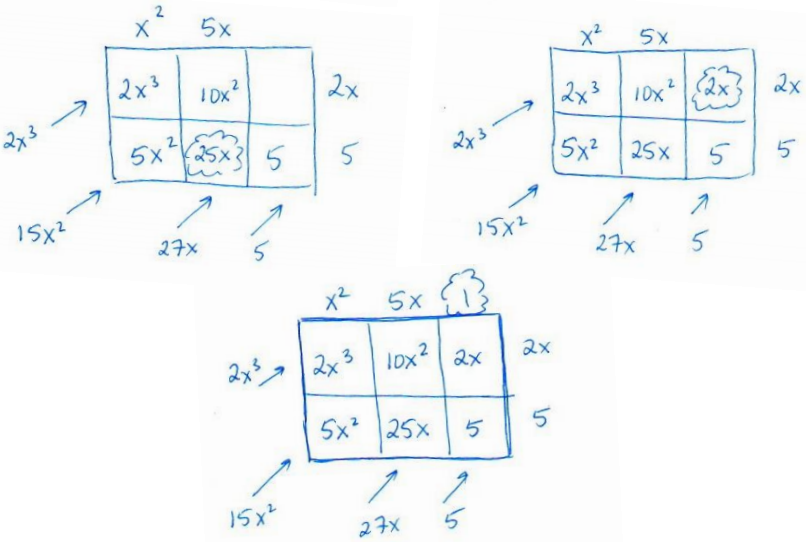
Question 3.
Reverse the tabular method of multiplication to find the quotient: \(\frac{2 x^{2}+x-10}{x-2}\)

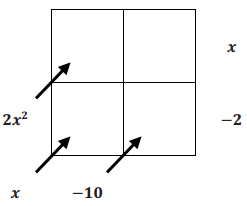
Answer:

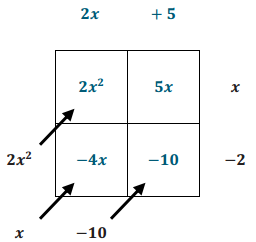
Question 4.
Test your conjectures. Create your own table, and use the reverse tabular method to find the quotient.
\(\frac{x^{4}+4 x^{3}+3 x^{2}+4 x+2}{x^{2}+1}\)
Answer:

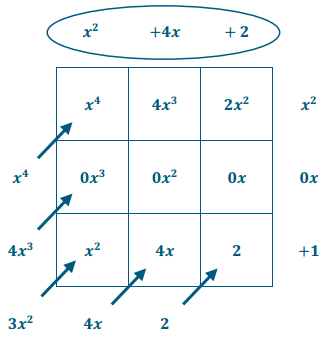
The quotient is x² + 4x + 2.

Question 5.
Test your conjectures. Use the reverse tabular method to find the quotient.
\(\frac{3 x^{5}-2 x^{4}+6 x^{3}-4 x^{2}-24 x+16}{x^{2}+4}\)
Answer:
The quotient is 3x³ – 2x² – 6x + 4.

Question 6.
What is the quotient of \(\frac{x^{5}-1}{x-1}\)? What is the quotient of \(\frac{x^{6}-1}{x-1}\)?
Answer:
The quotients are x⁴ + x³ + x² + x + 1 and x⁵ + x⁴ + x³ + x² + x + 1, respectively.

After students complete Exercise 6, see if they can extend the patterns to make
predictions about similar problems.
→ What is the result of dividing \(\frac{x^{8}-1}{x-1}\)?
→ x⁷ + x⁶ + x⁵ + x⁴ + x³ + x² + x + 1
→ What is the result of dividing \(\frac{x^{n}-1}{x-1}\)?
→ x^n-1 + x^n-2 + ………. + x + 1
→ What is the result of dividing \(\frac{x^{5}+1}{x+1}\)
→ x⁴ – x³ + x² – x + 1