Engage NY Eureka Math Algebra 2 Module 1 Lesson 1 Answer Key
Eureka Math Algebra 2 Module 1 Lesson 1 Example Answer Key
Example 1.
What is the sequence of first differences for the linear polynomial given by ax + b, where a and b are constant coefficients?
Answer:
The terms of the first differences sequence are found by subtracting consecutive terms in the sequence generated by the polynomial expression ax + b, namely,
{b, a + b, 2a + b, 3a + b,4a + b, ……….}.
1st term: (a + b) – b = a,
2nd term: (2a + b) – (a + b) = a,
3rd term: (3a + b) – (2a + b) = a,
4th term: (4a + b) – (3a + b) = a.
The first differences sequence is {a, a, a, a, …}. For first-degree polynomial expressions, the first differences are constant and equal to a.
What is the sequence of second differences for ax + b?
Answer:
Since a – a = 0, the second differences are all 0. Thus, the sequence of second differences is {o, o, o, o, …..).
Example 2.
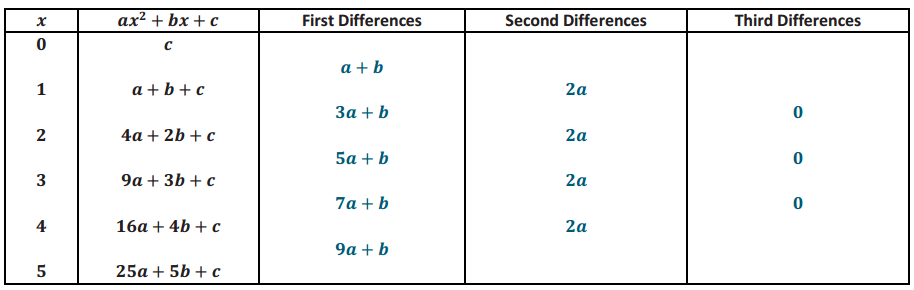
Find the first, second, and third differences of the polynomial ax2 + bx + c by filling in the blanks in the following table.

Answer:
Example 3.
Find the second, third, and fourth differences of the polynomial ax3 + bx2 + cx + d by filling in the blanks in the following table.
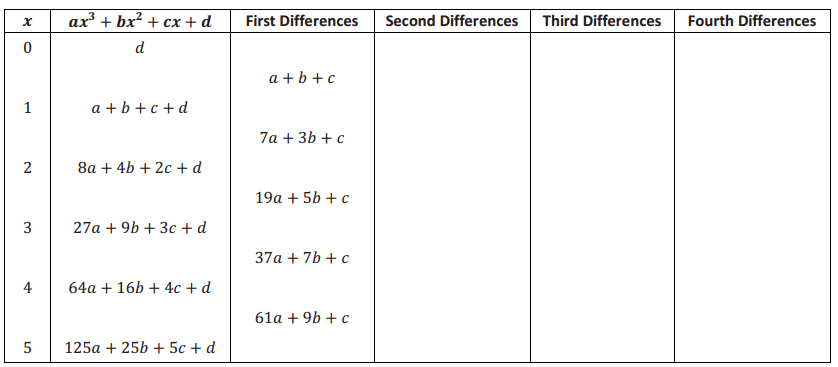
Answer:
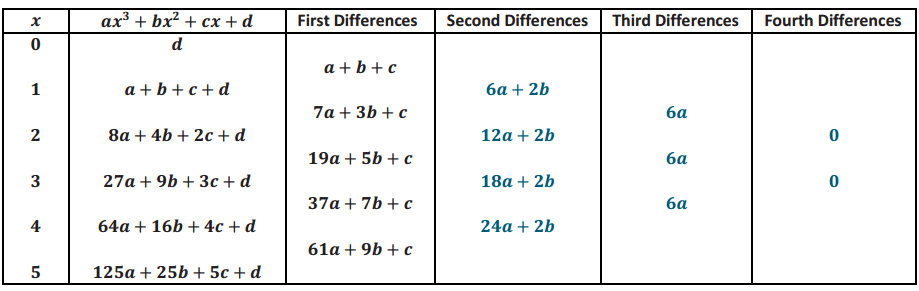
Example 4.
What type of relationship does the set of ordered pairs (x, y) satisfy? How do you know? Fill in the blanks in the table below to help you decide. (The first differences have already been computed for you.)
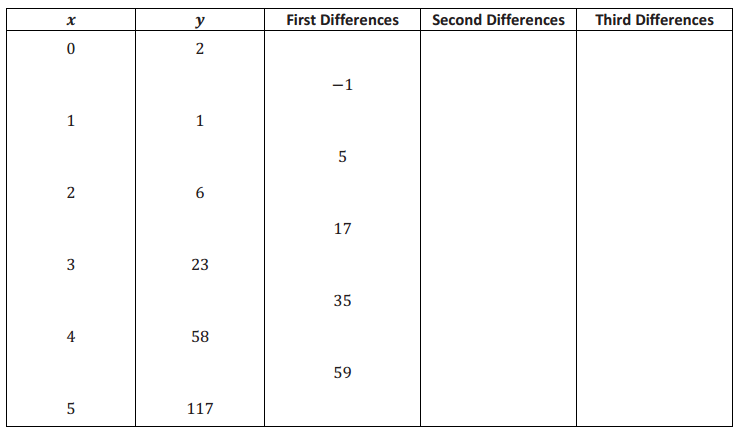
Answer:
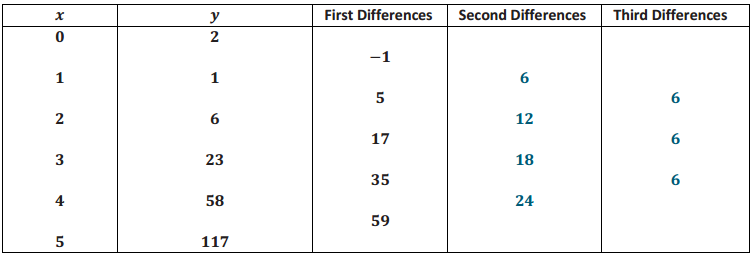
Since the third differences are constant, the pairs could represent a cubic relationship between x and y.
Find the equation of the form y = ax3 + bx2 + cx + d that all ordered pairs (x, y) above satisfy. Give evidence that your equation is correct.
Answer:
Since third differences of a cubic polynomial are equal to 6a, using the table above, we get 6a = 6, so that a = 1. Also, since (0, 2) satisfies the equation, we see that d = 2. Thus, we need only find b and c. Substituting (1, 1) and (2, 6) into the equation, we get
1 = 1 + b + c + 2
6 = 8 + 4b + 2c + 2.
Subtracting two times the first equation from the second, we get 4 = 6 + 2 b – 2,so that b = 0. Substituting 0 in for b in the first equation gives c = – 2. Thus, the equation is y = x3 – 2x + 2.
Eureka Math Algebra 2 Module 1 Lesson 1 Opening Exercise Answer Key
John noticed patterns In the arrangement of numbers in the table below.
Answer:
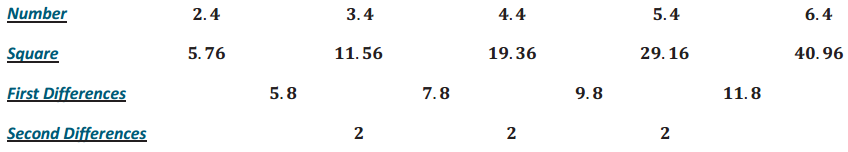
Assuming that the pattern would continue, he used It to find the value of 7. 42. Explain how he used the pattern to find 7. 42, and then use the pattern to find 8. 42.
Answer:
To find 7. 42, John assumed the next term in the first differences would have to be 13.8 since 13.8 is 2 more than 11.8. Therefore, the next term in the square numbers would have to be 40.96 + 13.8, which is 54.76. Checking with a calculator, we also find 7. 42 = 54.76.
To find 8. 42, we follow the same process: The next term in the first differences would have to be 15. 8, so the next term in the square numbers would be 54.76 + 15.8, which is 70.56.
Check: 8. 42 = 70.56.
How would you label each row of numbers in the table?
Answer:
Number, Square, First Differences, Second Differences
Discussion
Let the sequence {a0, a1, a2, a3, …..} be generated by evaluating a polynomial expression at the values 0, 1, 2, 3, … The numbers found by evaluating a1 – a0, a2 – a1, a3 – a2, … form a new sequence, which we will call the first differences of the polynomial. The differences between successive terms of the first differences sequence are called the second differences and so on.
Answer:
It is a good idea to use an actual sequence of numbers such as the square numbers {1, 4, 9, 16, …….} to help explain the meaning of the terms first differences and second differences.
Eureka Math Algebra 2 Module 1 Lesson 1 Problem Set Answer Key
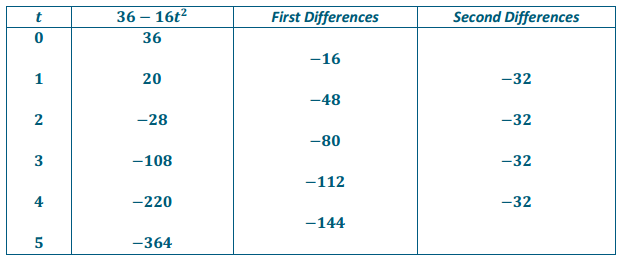
Question 1.
Create a table to find the second differences for the polynomial 36 – 16t2 for integer values of t from 0 to 5.
Answer:
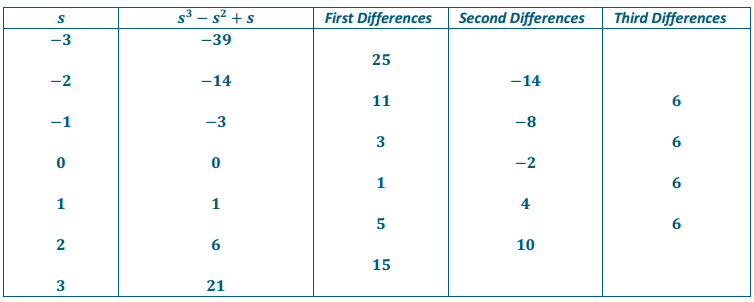
Question 2.
Create a table to find the third differences for the polynomial s3 – s2 + s for integer values of s from – 3 to 3.
Answer:
Question 3.
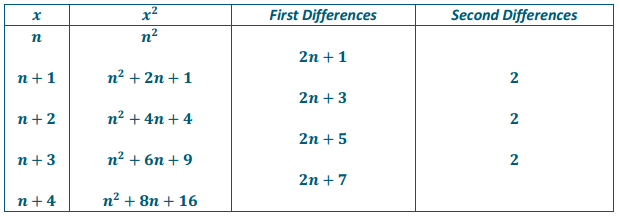
Create a table of values for the polynomial x2, using n, n + 1, n + 2, n + 3, n + 4 as values of x. Show that the second differences are all equal to 2.
Answer:
Question 4.
Show that the set of ordered pairs (x, y) in the table below satisfies a quadratic relationship. (Hint: Find second differences.) Find the equation of the form y = ax2 + bx + c that all of the ordered pairs satisfy.
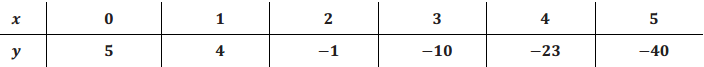
Answer:
Students show that second differences are constant and equal to – 4. The equation is y = – 2x2 + x + 5.
Question 5.
Show that the set of ordered pairs (x, y) in the table below satisfies a cubic relationship. (Hint: Find third differences.) Find the equation of the form y = ax3 + bx2 + cx + d that all of the ordered pairs satisfy.

Answer:
Students show that third differences are constant and equal to 12. The equation is y = 2x3 – 18x + 20.
Question 6.
The distance d ft. required to stop a car traveling at 10v mph under dry asphalt conditions is given by the following table.
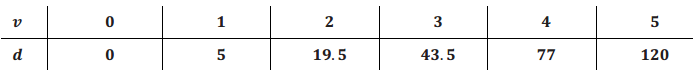
a What type of relationship is indicated by the set of ordered pairs?
Answer:
Students show that second differences are constant and equal to 9.5. Therefore the relationship is quadratic.
b Assuming that the relationship continues to hold, find the distance required to stop the car when the speed reaches 60 mph, when v = 6.
Answer:
172.5 ft
c. Extension: Find an equation that describes the relationship between the speed of the car v and its stopping distance d.
Answer:
d = 4.75v2 + 0.25v (Note: Students do not need ta Ibid the equatIon to answer part (b).)
Question 7.
Use the polynomial expressions 5x2 + x + 1 and 2x + 3 to answer the questions below.
a. Create a table of second differences for the polynomial 5x2 + x + 1 for the Integer values of x from 0 to 5.
Answer:
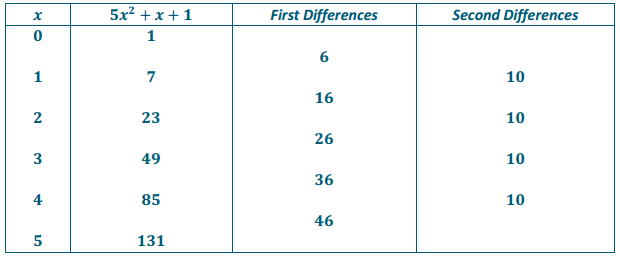
b. Justin claims that for n ≥ 2, the n differences of the sum of a degree n polynomial and a linear polynomial are the same as the nth differences of just the degree n polynomial. Find the second differences for the sum (5x2 + x + 1) + (2x + 3) of a degree 2 and a degree 1 polynomial, and use the calculation to explain why Justin might be correct in general.
Answer:
Students compute that the second differences are constant and equal to 10, just as in part (a). Justin is
correct because the differences of the sum are the sum of the differences. Since the second (and all other
higher) differences of the degree 1 polynomial are constant and equal to zero, only the nth differences of the degree n polynomial contribute to the nth difference of the sum.
c. Jason thinks he can generalize Justin’s claim to the product of two polynomials. He claims that for n ≥ 2, the (n + 1)st differences of the product of a degree n polynomial and a linear polynomial are the same as the n differences of the degree n polynomial. Use what you know about second and third differences (from Examples 2 and 3) and the polynomial (5x2 + x + 1)(2x + 3) to show that Jason’s generalization is incorrect.
Answer:
The second differences of a quadratic polynomial are 2a, so the second differences of 5x2 + x + 1 are always 10. Since (5x2 + x + l)(2x + 3) = 10x3 + 17x2 + 5x + 3, and third differences are equal to 6a, we have that the third differences of (5x2 + x + 1)(2x + 3) are always 60, which is not 10.
Eureka Math Algebra 2 Module 1 Lesson 1 Exit Ticket Answer Key
Question 1.
What type of relationship is indicated by the following set of ordered pairs? Explain how you know.
| X | Y |
| 0 | 0 |
| 1 | 2 |
| 2 | 10 |
| 3 | 24 |
| 4 | 44 |
Answer:
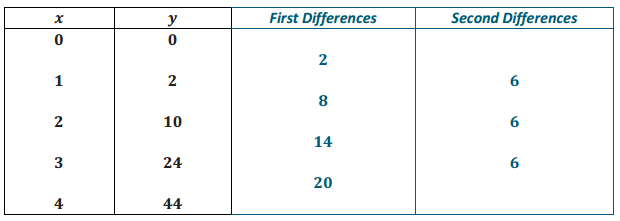
Since the second differences are constant, there is a quadratic relationship between x and y.
Question 2.
Find an equation that all ordered pairs above satisfy.
Answer:
Since (0, 0) satisfies an equation of the form y = ax2 + bx + c, we have that c = 0. Using the points (1, 2) and (2, 10), we have
2 = a + b
10 = 4a + 2b
Subtracting twice the first equation from the second gives 6 = 2a, which means a = 3. Substituting 3 into the first equation gives b = – 1. Thus, y = 3x2 – x is the equation.
OR
Since the pairs satisfy a quadratic relationship, the second differences must be equal to 2a. Therefore, 6 = 2a, so a = 3. Since (0, 0) satisfies the equation, c = 0. Using the point (1, 2), we have that 2 = 3 + b + 0, so b = – 1 Thus, y = 3x2 – x is the equation that is satisfied by these points.