Engage NY Eureka Math Algebra 1 Module 4 Lesson 9 Answer Key
Eureka Math Algebra 1 Module 4 Lesson 9 Example Answer Key
Example 1.
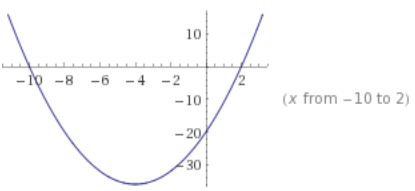
Consider the equation y = x2 + 6x – 40.
a. Given this quadratic equation, can you find the point(s) where the graph crosses the x – axis?
Answer:
The factors for x2 + 6x – 40 are (x – 4)(x + 10), so the solutions for the equation with y = 0 are x = 4 or x = – 10.
b. In the last lesson, we learned about the symmetrical nature of the graph of a quadratic function. How can we use that information to find the vertex for the graph?
Answer:
Since the x – value of the vertex is halfway between the two roots, we just need to find the midpoint of the two roots’ x – values: \(\frac{4 + ( – 10)}{m}\) = – 3. Once students know the x – value of the vertex (which also tells us the equation for the axis of symmetry), they can substitute that value back into the equation:
y = (x – 4)(x + 10). Thus, y = ( – 3 – 4)( – 3 + 10) = ( – 7)(7) = – 49, and the vertex is ( – 3, – 49).
c. How could we find the y – intercept (where the graph crosses the y – axis and where x = 0)?
Answer:
If we set x equal to 0, we can find where the graph crosses the y – axis.
y = (x – 4)(x + 10) = (0 – 4)(0 + 10) = ( – 4)(10) = – 40
The y – intercept is (0, – 40).
d. What else can we say about the graph based on our knowledge of the symmetrical nature of the graph of a quadratic function? Can we determine the coordinates of any other points?
Answer:
We know that the axis of symmetry is at x = – 3 and that 0 is 3 units to the right of – 3. Because the graph of a quadratic function is symmetrical, there exists another point with an x – coordinate 3 units to the left of – 3, which would be x = – 6. The points with x – coordinates of 0 and – 6 will have the same y – coordinate, which is – 40. Therefore, another point on this graph would be ( – 6, – 40).
e. Plot the points you know for this equation on graph paper, and connect them to show the graph of the equation.
Answer:
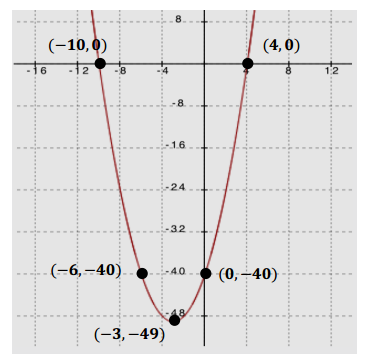
Example 2.
Consider the graph of the quadratic function shown below with x – intercepts – 4 and 2.
a. Write a formula for a possible quadratic function, in factored form, that the graph represents using a as a constant factor.
Answer:
f(x) = a(x + 4)(x – 2)
b. The y – intercept of the graph is – 16.
Answer:
Use the y – intercept to adjust your function by finding the constant factor a.
f(0) = a(0 + 4)(0 – 2) = – 16 → a = 2
f(x) = 2(x + 4)(x – 2)
Example 3.
A science class designed a ball launcher and tested it by shooting a tennis ball straight up from the top of a 15 – story building. They determined that the motion of the ball could be described by the function:
h(t) = – 16t2 + 144t + 160,
where t represents the time the ball is in the air in seconds and h(t) represents the height, in feet, of the ball above the ground at time t. What is the maximum height of the ball? At what time will the ball hit the ground?
a. With a graph, we can see the number of seconds it takes for the ball to reach its peak and how long it takes to hit the ground. How can factoring the expression help us graph this function?
Answer:
Change the expression to factored form. First, factor out the – 16 (GCF): – 16(t2 – 9t – 10). Then, we can see that the quadratic expression remaining is factorable: – 16(t + 1)(t – 10).
b. Once we have the function in its factored form, what do we need to know in order to graph it? Now graph the function.
Answer:
We can find the t – intercepts, y – intercept, axis of symmetry, and the vertex and then sketch the graph of the function. t – intercepts are (10, 0) and ( – 1, 0); y – intercept is (0, 160); the axis of symmetry is t = 4.5; and the vertex is (4.5, 484). (We find the y – coordinate of the vertex by substituting 4.5 into either form of the equation.)

Answer:
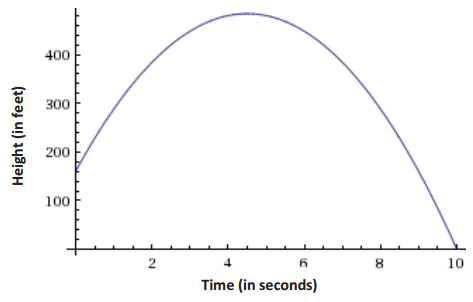
c. Using the graph, at what time does the ball hit the ground?
Answer:
10 seconds
d. Over what domain is the ball rising? Over what domain is the ball falling?
Answer:
The ball is rising from 0 to 4.5 seconds (0, 4.5). It is falling from 4.5 seconds to 10 seconds (4.5, 10). 4.5 is the t -value of the vertex of the graph, and for this context it represents the time that the ball reaches its highest point, and then it begins to fall toward the ground. At t = 10, the graph has an h – value of 0, so in this context, it represents the time that the ball hits the ground and stops descending.
e. Using the graph, what is the maximum height the ball reaches?
Answer:
484 ft. (See work above.)
Eureka Math Algebra 1 Module 4 Lesson 9 Exercise Answer Key
Opening Exercise
Solve the following equation.
x2 + 6x – 40 = 0
Answer:
The factored form is (x + 10)(x – 4) = 0, so x = – 10 or 4.
Exercise 1.
Graph the following functions, and identify key features of the graph.
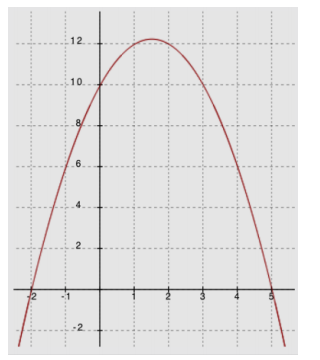
a. f(x) = – (x + 2)(x – 5)
Answer:
Key features: x – intercepts ( – 2, 0) (5, 0); vertex at x = 1.5 (1.5, 12.25); y – intercept (0, 10); end behavior: this graph opens down (as x approaches ±∞, y approaches – ∞)
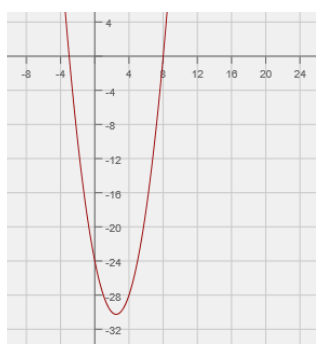
b. g(x) = x2 – 5x – 24

Answer:
Key features: x – intercepts ( – 3, 0) (8, 0); vertex at x = 2.5 (2.5, – 30.25); y – intercept (0, – 24); end – behavior: this graph opens up (as x approaches ±∞, y approaches ∞)
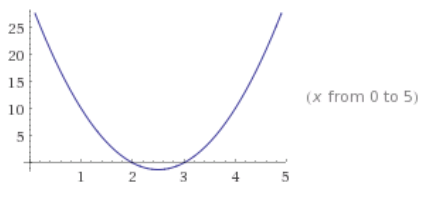
c. f(x) = 5(x – 2)(x – 3)

Answer:
Key features: x – intercepts are (2, 0) and (3, 0); vertex is where x = 2.5: (2.5, – 1.25); and the y – intercept is (0, 30); end behavior: this graph opens up (as x approaches ±∞, y approaches ∞).
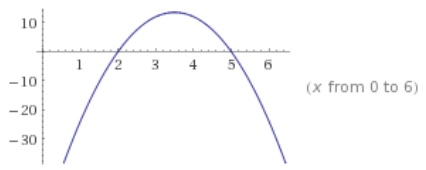
d. p(x) = – 6x2 + 42x – 60

Answer:
Factored form: p(x) = – 6(x – 5)(x – 2) Key features: x – intercepts are (5, 0) and (2, 0); the y – intercept is (0, – 60); the axis of symmetry is at x = 3.5; the vertex is (3.5, 13.5); end behavior: this graph opens down (as x approaches ±∞, y approaches – ∞).
Exercise 2.
Given the x – intercepts for the graph of a quadratic function, write a possible formula for the quadratic function, in factored form.
a. x – intercepts: 0 and 3
Answer:
f(x) = ax(x – 3)
b. x – intercepts: – 1 and 1
Answer:
f(x) = a(x + 1)(x – 1)
c. x – intercepts: – 5 and 10
Answer:
f(x) = a(x + 5)(x – 10)
d. x – intercepts: \(\frac{1}{2}\) and 4
Answer:
f(x) = a(x – \(\frac{1}{2}\))(x – 4)
Exercise 3.
Consider the graph of the quadratic function shown below with x – intercept – 2.
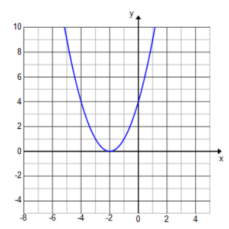
a. Write a formula for a possible quadratic function, in factored form, that the graph represents using a as a constant factor.
Answer:
f(x) = a(x + 2)(x + 2) or f(x) = a(x + 2)2
b. The y – intercept of the graph is 4.
Use the y – intercept to adjust your function by finding the constant factor a.
Answer:
f(0) = a(0 + 2)(0 + 2) = 4 → a = 1
f(x) = (x + 2)(x + 2) or f(x) = (x + 2)2
Exercise 4.
The science class in Example 3 adjusted their ball launcher so that it could accommodate a heavier ball. They moved the launcher to the roof of a 23 – story building and launched an 8.8 – pound shot put straight up into the air. (Note: Olympic and high school women use the 8.8 – pound shot put in track and field competitions.) The motion is described by the function h(t) = – 16t2 + 32t + 240, where h(t) represents the height, in feet, of the shot put above the ground with respect to time t in seconds. (Important: No one was harmed during this experiment!)

a. Graph the function, and identify the key features of the graph.

Answer:
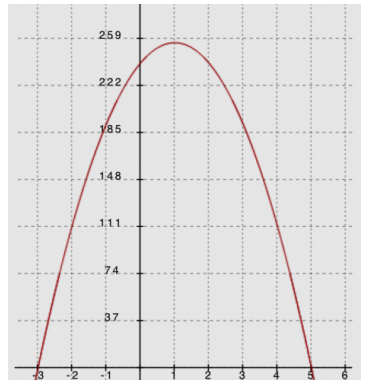
Key features: Vertex: (1, 256); t – intercepts: (5, 0) and ( – 3, 0); y – intercept: (0, 240)
b. After how many seconds does the shot put hit the ground?
Answer:
The factored form of the function: h(t) = – 16(t – 5)(t + 3), so the positive zero of the function is (5, 0), and the shot put hits the ground at 5 seconds.
c. What is the maximum height of the shot put?
Answer:
The vertex is found where t = 1, so the vertex is (1, 256), and the shot put reaches a maximum height at 256 ft.
d. What is the value of h(0), and what does it mean for this problem?
Answer:
h(0) = 240. This means that the shot put’s initial height was 240 ft above the ground.
Eureka Math Algebra 1 Module 4 Lesson 9 Problem Set Answer Key
Question 1.
Graph the following on your own graph paper, and identify the key features of the graph.
a. f(x) = (x – 2)(x + 7)
Answer:
Key features: x – intercepts (2, 0) and ( – 7, 0); y – intercept (0, – 14); vertex at x = – 2.5 ( – 2.5, – 20.25).
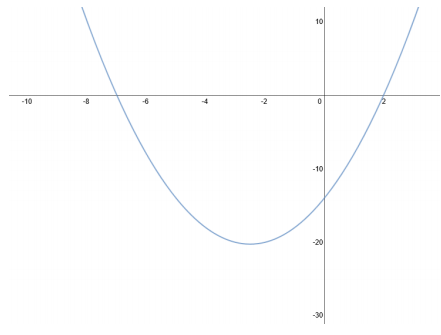
b. h(x) = – 3(x – 2)(x + 2)
Answer:
Key features: vertex (0, 12); axis of symmetry at x = 0; y – intercept (0, 12); x – intercepts ( – 2, 0) and (2, 0).
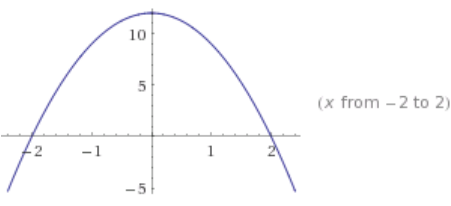
c. g(x) = – 2(x – 2)(x + 7)
Answer:
Key features: x – intercepts (2, 0) and ( – 7, 0); vertex is where x = – 2.5 ( – 2.5, 40.5); y – intercept is (0, 28).
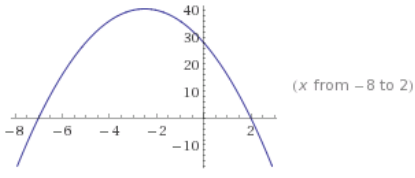
d. h(x) = x2 – 16
Answer:
Key features: x – intercepts (4, 0) and ( – 4, 0); y – intercept and vertex are both (0, – 16).
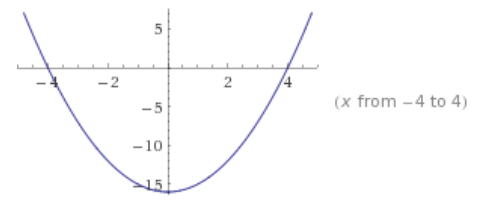
e. p(x) = x2 – 2x + 1
Answer:
Key features: x – intercept is a double root and is also the vertex (1, 0); the y – intercept is (0, 1).
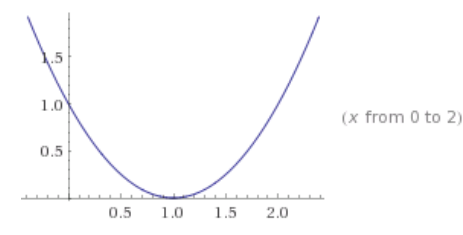
f. q(x) = 4x2 + 20x + 24
Answer:
Factored form: q(x) = 4(x2 + 5x + 6) = 4(x + 2)(x + 3); x – intercepts ( – 2, 0) and ( – 3, 0); y – intercept (0, 24); vertex is where x = – 2.5 at the point ( – 2.5, – 1).
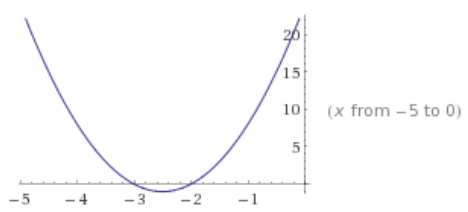
Question 2.
A rocket is launched from a cliff. The relationship between the height of the rocket, h, in feet, and the time since its launch, t, in seconds, can be represented by the following function:
h(t) = – 16t2 + 80t + 384.
a. Sketch the graph of the motion of the rocket.
Answer:
Key features: factored form is h(t) = – 16(t2 – 5t – 24) = – 16(t – 8)(t + 3); t – intercepts (8, 0) and ( – 3, 0); y – intercept (0, 384); vertex at t = 2.5 (2.5, 484).
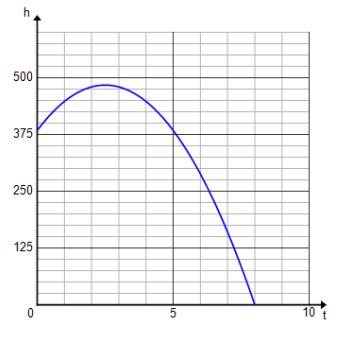
b. When does the rocket hit the ground?
Answer:
The rocket will hit the ground after 8 seconds. The zeros of the function are at t = – 3 and 8. Since the rocket was in the air from t = 0, it would be airborne for 8 seconds.
c. When does the rocket reach its maximum height?
Answer:
The rocket will reach its maximum height after 2.5 seconds. The t – coordinate of the vertex, the highest point on the graph, is at t = 2.5.
d. What is the maximum height the rocket reaches?
Answer:
The maximum height is 484 ft. The vertex, which is the maximum point, is at (2.5, 484).
e. At what height was the rocket launched?
Answer:
The rocket was launched from a height of 384 ft. This is the height of the rocket at time t = 0.
Question 3.
Given the x – intercepts for the graph of a quadratic function, write a possible formula for the quadratic function, in factored form.
a. x – intercepts: – 1 and – 6
Answer:
f(x) = a(x + 1)(x + 6)
b. x – intercepts: – 2 and \(\frac{2}{3}\)
Answer:
f(x) = a(x + 2)(x – \(\frac{2}{3}\))
c. x – intercepts: – 3 and 0 d. x – intercept: 7
Answer:
f(x) = ax(x + 3)
d. x – intercept: 7
Answer:
f(x) = a(x – 7)(x – 7) or f(x) = a(x – 7)2
Question 4.
Suppose a quadratic function is such that its graph has x – intercepts of – 3 and 2 and a y – intercept of 6.
a. Write a formula for the quadratic function.
Answer:
f(x) = – (x + 3)(x – 2)
b. Sketch the graph of the function.
Answer:
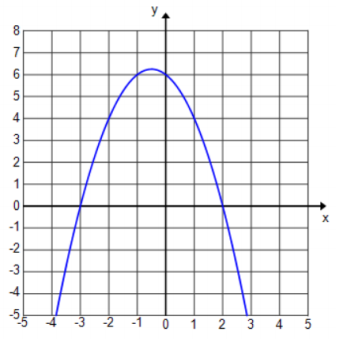
Eureka Math Algebra 1 Module 4 Lesson 9 Exit Ticket Answer Key
Question 1.
Graph the following function, and identify the key features of the graph: t(x) = x2 + 8x – 20.

Answer:
Factored form: t(x) = (x + 10)(x – 2), so the
x – intercepts are ( – 10, 0) and (2, 0); the y – intercept is (0, – 20); and the vertex is where x = – 4: ( – 4, – 36); end behavior: this graph opens up (as x approaches ±∞, the y – value approaches ∞).