In this article, you will learn the concept of the equation of a straight line. In geometry, the equation of a straight line is the most commonly used. There are different forms for finding the equation of a straight line such as point-slope form, slope-intercept form, general form, standard form, etc. A straight line is a two-dimensional geometrical entity it can be extended on both of its ends to infinity.
On this page, we will discuss the 10th Grade Math concept of the equation of a straight line. Try to make you understand the equation of a line, the straight-line formula, how to find the equation of a straight line, and other interesting aspects of it. Also, Solving a few interesting example questions which will help to better understand the concept.
Also, Read:
What is meant by the Equation of Straight Line?
The equation of a straight line is defined as which gives the relation between the coordinate points lying on that straight line. It will be in different forms and which tell the slope of the x-intercept, and the y-intercept of the line. The most commonly used equation of straight lines form is,
y = mx + c
In another form, it will be ax + by = c.
If the product of slopes of the two straight lines is -1, then the lines are perpendicular to each other. If the two straight lines are parallel to each other, then they have the same slope.
Equation of a Straight Line – Formula
In a straight line, when two points A (x1, y1) and B (x2, y2) are connected with a minimum distance between them, both the ends are extended to infinity. The equation of a straight is also a linear equation. The standard form of a linear equation with a variables x and y is,
ax + by = c.
In this equation, x and y are variables, and a, b, and c are constants.
A few more Equation of Straight Line formulas are,
- The equation of a straight line in standard Form is ax+by = c
- The equation of a line in Slope-Intercept Form is y = mx+c
- The equation of a line in Point-slope Form is y-y1 = m(x-x1)
Equation of a Straight Line in Different Forms
Consider a line L makes an angle of θ with a positive direction of the x-axis and the angle θ is known as the inclination of the line and the tan θ will be the slope of the line. Remember that the x-axis has a slope of 0. If all the lines are parallel to the x-axis then the slope is 0. If the slope of all the vertical lines is included in the y-axis will not be defined. We know the basic form of the equation of a line, now see the different forms of equations of a straight line is,
Standard Form of Equation of Line:
The standard form of the equation of a straight line is given by ax + by = c, where a, b, and c are the real numbers. Consider an example that transfers the equation y = 2x – 1 in the standard form. Now, subtract 2x from both sides of the equation then we get
y – 2x = 2x – 1 – 2x
⇒ y – 2x = -1
⇒ 2x – y = 1
Therefore, the generated standard form of the equation of the line is 2x – y = 1.
Point-Slope Form:
The equation of a straight line whose slope is m and which passes through a point (x1, y1) is found using the point-slope form. The equation for point-slope form is,
y – y1 = m (x – x1)
where the (x, y) is an arbitrary point on the line. The point-slope form is shown below,
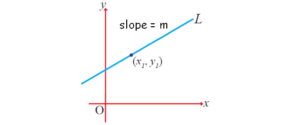
How to find the Equation of Straight Line Given Two Points?
Here, we will discuss how to find the equation of a straight line using the point-slope form. First, derive this formula using the equation for the slope of a line. Considering that the line slope is m. Assume that (x1, y1) is known as the point on the line. The intercept (x, y) is any other points on the line whose coordinates are not known. We know the equation for the slope of a line is,
Slope = Difference in y-coordinates / Difference in x-coordinates
that is m = (y – y1)/(x – x1)
Now, multiply both sides by (x – x1),then it will be
m (x – x1) = (y – y1)
It can be rewrite as,
(y – y1) = m (x – x1)
Thus, the equation of a line using the point-slope form is proved.
Slope-Intercept Form:
Consider a line with its slope is m and it is the y-intercept. It says that the line intersects the y-axis at the point (0, c). Using this point-slope form we have y – c = m (x – 0) that is Y = mx + c, where c will be the y-intercept. For that, if d is the x-intercept, then the slope-intercept form of the equation of the line is,
y = m(x – d). The slope-intercept form of a straight line figure is as shown below,
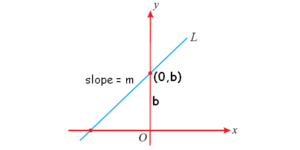
Equation of a Straight Line Graph
The graph of a linear equation in which one variable is x which forms a vertical line parallel to the y-axis and the equation of a straight line graph in which another variable is y which is a horizontal line parallel to the x-axis. A linear equation in which two variables x and y form a straight line on a graph. The Equation of a straight line using a graph is shown below,
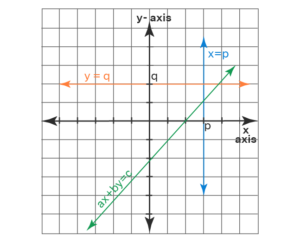
Equation of Straight Line Examples
Example 1: What is the equation of a straight line that passes through the points (1,5) and (-3, 6).
Solution:
Given that, the points are (1,5) and (-3, 6).
So, we will use the point-slope form formula to find the equation.
First, we need to find out the slope of the line.
The Slope is (6-5)/(-3-1) = 1/-4.
Therefore, the equation of the line passing through (1, 5) and (-3, 6) is y – 6 = (1/-4) (x + 3)
⇒ y – 6 = x/-4 + 3/3
⇒ y + x/-4 = 6 + 3/3
⇒ x – 4y = 7
So, the required equation of a straight line is x – 4y = 7.
Example 2: The equation of a line is given by 2x – 6y +3 = 0. Find the slope of both intercepts?
Solution:
As given in the question, the equation is 2x – 6y + 3 = 0.
Now, it can be represented in slope-intercept form as:
y = x/3 + 1/2
Now Compare the equation with y = mx + c,
So, the slope of the line is m = 1/3.
Now, the above equation will be rewrite in the intercept form as,
x/a + y/b = 1
2x – 6y = -3
x/(-3/2) – y/(-1/2) = 1
Thus, the x-intercept is given as a = -3/2 and the y-intercept is b = 1/2.
Problem 3: The equation of a line is given by, 15x – y + 11 = 0. What are the slope and both the intercepts?
Solution:
The given equation is 15x – y + 11 = 0
The equation is represented in slope-intercept form as,
y = 15x + 11
Now, comparing it with y = mx + c,
The slope of the line m is 15.
Rewrite the above equation in the intercept form as,
x/a + y/b = 1
15x – y = -11
x/(-11/15) + y/11 = 0
Hence, the x-intercept is given as a = -11/15 and the y-intercept as b = 11.
Problem 4: Find the equation of the line whose gradient is 3/2 and which passes through P, where P divides the line segment joining A(-2, 6) and B (3, -4) in the ratio 2 : 3 internally.
Solution:
Given that, the line segment joining at A(-2,6) and B(3,-4)
Now, we need to find out the point P.
So, the formula is P = (lx₂ + mx₁)/(l + m), (ly₂ + my₁)/(l + m)
Substitute the values in the formula. We get,
P = (2(3) + 3(-2))/(2+3), (2(-4) + 3(6))/(2+3)
= (6 -6)/5, (-8 + 18)/5
= 0/5, 10/5
P = (0, 2)
Next, the (x₁, y₁) is (0, 2)
That is m = 3/2.
(y – y₁) = m(x – x₁)
Place y1 value in the above equation.
(y – 2) = (3/2)(x – 0)
2(y – 2) = 3x
2y – 4 = 3x
3x – 2y + 4 = 0
Thus, the required equation is 3x – 2y + 4 = 0.
Problem 5: What is the equation of the straight lines parallel to the coordinate axes and passing through the point (3, -4).
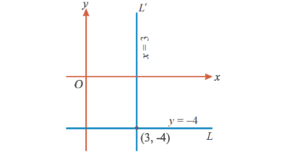
Solution:
Let L and L’ be the straight lines passing through the point (3, -4) and parallel to the x-axis and y-axis respectively.
At every point, the y-coordinates on the line L are – 4.
So, the equation of the line L is y = -4
Next, the x-coordinate of every point on the straight line L’ is 3.
Therefore, the equation of the line L’ is x = 3.
Problem 6: What is the general equation of the straight line whose angle of inclination is 45° and y-intercept is 2/5?
Solution:
In the given question, the angle of inclination is 45°
We can get the slope from the angle of inclination of 45°
So, the slope of the line m is tan45°
So, the value of m is 1.
Next, the given y-intercept b is 2/5.
We know that, the Equation of a straight line in the slope-intercept form as,
y = mx + b
Substitute the value of m = 1 and b = 2/5.
Then the value of y is x + 2/5.
Now, multiply each side by 5.
5y = 5x + 2
Subtract 5y from each side,
0 = 5x – 5y + 2
5x – 5y + 2 = 0
Hence, the general equation of straight line is 5x – 5y + 2 = 0.
FAQ’s on Equation of a Straight Line
1. What are the conditions for a straight line?
In geometry, a line is simply an object which is characterized by a zero-width object that extends on both end sides. A straight line is just a line with has no curves. So, the line that extends to both sides till infinity and has no curves is called a straight line.
2. What is meant by the equation of a straight line?
The equation y = mx + c is the general equation of any straight line where m is the gradient of the line (how steep the line is) and c will be the y-intercept (the point at which the line crosses the y -axis).
3. What is the use of a straight-line equation?
The equation of a straight line is a mathematical equation that gives the relation between the coordinate points lying on the straight line. The general equation of a straight line is y = mx + c, where m is the slope of the line and c is the y-intercept.
4. What are the properties of a straight line?
The Properties of a Straight Line is
- A straight line has zero areas and zero volume. but it has infinite length.
- A straight line is a one-dimensional figure.
- It has an infinite number of lines that can pass through a single point, but there is only one unique line that passes through two points.
