Into Math Grade 5 Module 6 Lesson 1 Answer Key Represent Fraction Sums and Differences

We included HMH Into Math Grade 5 Answer Key PDF Module 6 Lesson 1 Represent Fraction Sums and Differences to make students experts in learning maths.

HMH Into Math Grade 5 Module 6 Lesson 1 Answer Key Represent Fraction Sums and Differences

I Can make a visual model to represent the addition or subtraction of fractions with different-sized parts.

Spark Your Learning

Four hikers travel along the same trail over two days. The fraction of the trail each hiker travels is shown.

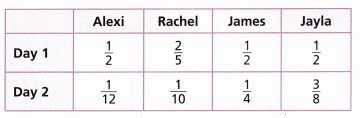
Use the data in the table to show two ways to represent the fraction of the trail one of the hikers travels on both days.

Answer:
Alexi: \(\frac{1}{2}\) + \(\frac{1}{12}\)
\(\frac{1}{2}\) + \(\frac{1}{12}\)  = \(\frac{6}{12}\) + \(\frac{1}{12}\) = \(\frac{7}{12}\)
Rachel: \(\frac{2}{5}\) + \(\frac{1}{10}\)  = \(\frac{4}{10}\) + \(\frac{1}{10}\) = \(\frac{5}{10}\) = \(\frac{1}{2}\)
James: \(\frac{1}{2}\) + \(\frac{1}{4}\)  = \(\frac{2}{4}\) + \(\frac{1}{4}\) = \(\frac{3}{4}\)
Jayla: \(\frac{1}{2}\) + \(\frac{3}{8}\)  = \(\frac{4}{8}\) + \(\frac{3}{8}\) = \(\frac{7}{8}\)

Turn and Talk Compare your ways with the ways of your classmates. How are they the same? How are they different?

Build Understanding

1. Marley and Jackie save together to buy a tent for their camping trip. Marley saves \(\frac{3}{8}\) of the cost of the tent. Jackie saves \(\frac{1}{2}\) of the cost of the tent. How much do Marley and Jackie save toward the cost of the tent?

How can you represent the situation?
Draw to show your thinking.

A. How did you combine \(\frac{3}{8}\) and \(\frac{1}{2}\) to help you find how much Marley and Jackie save? Explain your thinking.

B. Write an equation to model your solution.
Answer:
Given,
Marley and Jackie save together to buy a tent for their camping trip. Marley saves \(\frac{3}{8}\) of the cost of the tent.
Jackie saves \(\frac{1}{2}\) of the cost of the tent.
\(\frac{3}{8}\) + \(\frac{1}{2}\) = c
\(\frac{3}{8}\) + \(\frac{4}{8}\) = \(\frac{7}{8}\)
So, Marley and Jackie save \(\frac{7}{8}\)

Turn and Talk How could you have solved this problem another way? Compare your answer with those of your classmates.

2. Pedro takes a \(\frac{1}{2}\)-pound bag of trail mix on his hike. During the hike, he eats \(\frac{1}{4}\) pound of the trail mix. How much trail mix does he have left?
A. How can you use fraction strips to represent the situation? Draw to show your thinking.
B. What size fraction strip pieces can you use to represent the amount of trail mix he has left?
C. Write an equation to model the amount of trail mix he has left. What is the amount? _____
Answer:
Given,
Pedro takes a \(\frac{1}{2}\)-pound bag of trail mix on his hike.
During the hike, he eats \(\frac{1}{4}\) pound of the trail mix.
\(\frac{1}{2}\) – \(\frac{1}{4}\) = \(\frac{1}{4}\) pound
Thus he has left \(\frac{1}{4}\) pound of the trail mix.

Turn and Talk Suppose Pedro has \(\frac{3}{4}\) pound of trail mix at the start of the hike and he eats \(\frac{1}{3}\) pound. How can you find the amount of
trail mix he has left using fraction strips? How does this fraction model compare to the one you used in the problem above?

Check Understanding Math Board

Question 1.
Claudia starts at the nature center and walks \(\frac{1}{2}\) mile along a trail to this signpost. How far is the waterfall from the nature center?

• How can you use fraction strips to represent the distance from the nature center to the waterfall? Draw to show your thinking.
  
• Write an equation to show the distance from the nature center to the waterfall. What is the distance?
  Answer:
  Given,
  Claudia starts at the nature center and walks \(\frac{1}{2}\) mile along a trail to this signpost.
  \(\frac{1}{2}\) + \(\frac{1}{12}\)  = \(\frac{6}{12}\) + \(\frac{1}{12}\) = \(\frac{7}{12}\)
  So, the distance from the nature center to the waterfall is \(\frac{7}{12}\) mile.

On Your Own

Question 2.
Model with Mathematics Luna hammers a stake into the ground for her tent. The stake is \(\frac{7}{8}\) foot long. She hammers the stake \(\frac{3}{4}\) foot into the ground.

• How long is the part of the stake that is above the ground? _____
• Draw to represent how you solved this problem. _________
• Write an equation to model the solution.
  ____________________

Answer:
Given,
Luna hammers a stake into the ground for her tent. The stake is \(\frac{7}{8}\) foot long.
She hammers the stake \(\frac{3}{4}\) foot into the ground.
\(\frac{7}{8}\) + \(\frac{3}{4}\)
LCD of 4 and 8 is 8.
\(\frac{7}{8}\) + \(\frac{6}{8}\) = \(\frac{13}{8}\)
Convert it into mixed fraction
\(\frac{13}{8}\) = 1\(\frac{5}{8}\) feet

Question 3.
Use Tools Tyler’s cell phone has \(\frac{7}{10}\) of its charge left at the start of his hike, and \(\frac{1}{5}\) at the end.

• How much of the phone’s charge is used during the hike?
• Draw to represent how you solved this problem.
  

Answer:
Tyler’s cell phone has \(\frac{7}{10}\) of its charge left at the start of his hike, and \(\frac{1}{5}\) at the end.
We can solve this problem by finding the difference between the fractions.
\(\frac{7}{10}\) – \(\frac{1}{5}\)
Find the LCD of 10 and 5 = 10.
\(\frac{7}{10}\) – \(\frac{2}{10}\) = \(\frac{5}{10}\) = \(\frac{1}{2}\)
\(\frac{1}{2}\) of the phone’s charge is used during the hike.

Question 4.
Reason Why is it important to represent fractions with the same-sized parts when adding and subtracting?
Answer:
The real reason is due to the definition of the fraction itself, which is a representation of parts of a total that must be the same size. When you add or subtract fractions, you can’t express the result as a fraction if you do not divide the total into equal parts.

I’m in a Learning Mindset!

How did collaborating with a classmate help me make good decisions when representing fraction sums and differences?
Answer:
Collaborating with my classmate helped me to find the LCD of the fractions and then add and subtract the fractions easily.