We included HMH Into Math Grade 5 Answer Key PDF Module 7 Lesson 2 Assess Reasonableness of Fraction Sums and Differences to make students experts in learning maths.
HMH Into Math Grade 5 Module 7 Lesson 2 Answer Key Assess Reasonableness of Fraction Sums and Differences
I Can add and subtract fractions with unlike denominators using a common denominator and assess reasonableness.
Step It Out
1. Jaime is building a bird feeder. He connects two metal rods together to make a stand. The blueprint for the project shows the lengths of the rods. What is the total length of the rods?
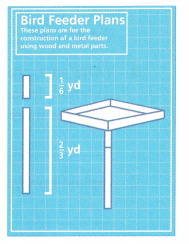
A. Write an expression to model the situation.
____________________
B. Find a common denominator for the fractions in this expression.
____________________
C. Write equivalent fractions using the common denominator.
____________________
D. Write an expression using fractions with a common denominator. Then find the total length of the rods.
____________________
E. Explain how you know your answer is reasonable.
Answer:
Given,
Jaime is building a bird feeder. He connects two metal rods together to make a stand.
The blueprint for the project shows the lengths of the rods.
\(\frac{1}{6}\) + \(\frac{2}{3}\)
\(\frac{1}{6}\) + \(\frac{4}{6}\) = \(\frac{5}{6}\)
The total length of the rods is \(\frac{5}{6}\) yards.
Turn and Talk Jon says you have to rewrite fractions with common denominators before you can estimate. Sarah says you can estimate without finding a common denominator first. Who do you think is correct and why?
Step It Out
2. Jaime fastens the bottom of the bird feeder to the pole. He has four boards that are each \(\frac{5}{6}\)-foot long. How much must Jaime cut from each board to make each side of the feeder \(\frac{3}{4}\)-foot long?
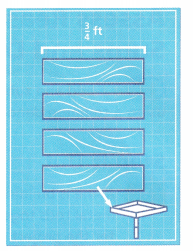
A. Write an expression you can use to solve the problem.
B. Write an expression using fractions with a common denominator to model the problem. Then find how much Jaime must cut from each board.
C. Explain how you know your answer is reasonable.
Answer:
\(\frac{5}{6}\) – \(\frac{3}{4}\)
The fractions have, unlike denominators. First, find the Least Common Denominator and rewrite the fractions with the common denominator.
LCD of 6 and 4 is 12.
\(\frac{10}{12}\) – \(\frac{9}{12}\) = \(\frac{1}{12}\)
Turn and Talk Look at the denominators of the given fractions. Note that neither denominator is a multiple of the other. How does this indicate that both fractions need to be renamed for them to have a common denominator?
Check Understanding Math Board
Question 1.
Jaime starts with \(\frac{7}{8}\) ounce of glue. After a project, \(\frac{1}{4}\) ounce of glue is left. Write an expression that can be used to find how much glue Jaime uses. Solve the problem. Show that your answer is reasonable.
Answer:
Given,
Jaime starts with \(\frac{7}{8}\) ounce of glue.
After a project, \(\frac{1}{4}\) ounce of glue is left.
\(\frac{7}{8}\) – \(\frac{1}{4}\)
\(\frac{7}{8}\) – \(\frac{2}{8}\) = \(\frac{5}{8}\) ounce
Write the expression using fractions with a common denominator. Then find the sum or difference.
Question 2.
\(\frac{2}{3}\) – \(\frac{1}{5}\) ____________________
Answer:
\(\frac{2}{3}\) – \(\frac{1}{5}\)
The fractions have, unlike denominators. First, find the Least Common Denominator and rewrite the fractions with the common denominator.
LCD of 3 and 5 is 15.
\(\frac{10}{15}\) – \(\frac{3}{15}\) = \(\frac{7}{15}\)
Question 3.
\(\frac{1}{6}\) + \(\frac{3}{4}\) ____________________
Answer:
\(\frac{1}{6}\) + \(\frac{3}{4}\)
The fractions have, unlike denominators. First, find the Least Common Denominator and rewrite the fractions with the common denominator.
LCD of 6 and 4 is 12.
\(\frac{2}{12}\) + \(\frac{9}{12}\) = \(\frac{11}{12}\)
On Your Own
Question 4.
Critique Reasoning Kyle is stringing a necklace with beads. He puts black beads on \(\frac{5}{8}\) of the string and white beads on \(\frac{1}{4}\) of the string. Kyle thinks that he will cover \(\frac{6}{12}\) of the string with beads. Is Kyle’s claim reasonable?
Answer:
Given,
Kyle is stringing a necklace with beads. He puts black beads on \(\frac{5}{8}\) of the string and white beads on \(\frac{1}{4}\) of the string.
\(\frac{5}{8}\) + \(\frac{1}{4}\)
LCD of 4 and 8 is 8.
\(\frac{5}{8}\) + \(\frac{2}{8}\) = \(\frac{7}{8}\)
Thus Kyle’s Claim is not reasonable.
Question 5.
STEM Precipitation can be in the form of rain, snow, sleet, or hail. In Sarasota, Florida, it rains about \(\frac{2}{3}\) inch on May 22 and about \(\frac{5}{12}\) inch on May 25.
- What expression represents the difference in the amount of rainfall for the two days?
- Write an expression using fractions with a common denominator. Then find the difference.
Answer:
Given,
Florida, it rains about \(\frac{2}{3}\) inch on May 22 and about \(\frac{5}{12}\) inch on May 25.
\(\frac{2}{3}\) – \(\frac{5}{12}\)
LCD of 3 and 12 is 12.
\(\frac{8}{12}\) – \(\frac{5}{12}\) = \(\frac{3}{12}\) = \(\frac{1}{4}\)
Write the expression using fractions with a common denominator. Then find the sum or difference.
Question 6.
\(\frac{3}{8}\) + \(\frac{1}{6}\)
Answer:
\(\frac{3}{8}\) + \(\frac{1}{6}\)
The fractions have, unlike denominators. First, find the Least Common Denominator and rewrite the fractions with the common denominator.
LCD of 8 and 6 is 24.
Multiply both the numerator and denominator of each fraction by the number that makes its denominator equal to the LCD.
\(\frac{3}{8}\) × \(\frac{3}{3}\) + \(\frac{1}{6}\) × \(\frac{4}{4}\)
\(\frac{9}{24}\) + \(\frac{4}{24}\) = \(\frac{13}{24}\)
Question 7.
\(\frac{3}{4}\) – \(\frac{7}{12}\)
Answer:
\(\frac{3}{4}\) – \(\frac{7}{12}\)
The fractions have, unlike denominators. First, find the Least Common Denominator and rewrite the fractions with the common denominator.
LCD of 4 and 12 is 12.
Multiply both the numerator and denominator of each fraction by the number that makes its denominator equal to the LCD.
\(\frac{3}{4}\) × \(\frac{3}{3}\) – \(\frac{7}{12}\) × \(\frac{1}{1}\)
\(\frac{9}{12}\) – \(\frac{7}{12}\) = \(\frac{2}{12}\) = \(\frac{1}{6}\)
Question 8.
\(\frac{1}{6}\) + \(\frac{3}{9}\)
Answer:
\(\frac{1}{6}\) + \(\frac{3}{9}\)
The fractions have, unlike denominators. First, find the Least Common Denominator and rewrite the fractions with the common denominator.
LCD of 6 and 9 is 18.
\(\frac{3}{18}\) + \(\frac{6}{18}\) = \(\frac{9}{18}\) = \(\frac{1}{2}\)
Question 9.
\(\frac{7}{9}\) – \(\frac{1}{3}\)
Answer:
\(\frac{7}{9}\) – \(\frac{1}{3}\)
The fractions have, unlike denominators. First, find the Least Common Denominator and rewrite the fractions with the common denominator.
LCD of 3 and 9 is 9.
\(\frac{7}{9}\) – \(\frac{3}{9}\) = \(\frac{4}{9}\)
Question 10.
Mr. Singh’s laptop memory is \(\frac{9}{10}\) full. After he deletes some files, the memory \(\frac{3}{5}\) is full.
- What faction represents the part of the laptop memory that he deletes? ______

- Is your answer reasonable? How do you know?
____________________
____________________
Answer:
Given,
Mr. Singh’s laptop memory is \(\frac{9}{10}\) full.
After he deletes some files, the memory \(\frac{3}{5}\) is full.
\(\frac{9}{10}\) – \(\frac{3}{5}\)
LCD of 10 and 5 is 10.
\(\frac{9}{10}\) – \(\frac{6}{10}\) = \(\frac{3}{10}\)
The fraction \(\frac{3}{10}\) represents the part of the laptop memory that he deletes.
Question 11.
Tracy checks the digital tablets made at a factory. In one box of tablets, she finds that \(\frac{1}{20}\) have a cracked screen. In the same box, she finds that another \(\frac{1}{5}\) have the wrong software. What fraction of the tablets in the box have either a cracked screen or the wrong software?

Answer:
Given,
Tracy checks the digital tablets made at a factory. In one box of tablets, she finds that \(\frac{1}{20}\) have a cracked screen.
In the same box, she finds that another \(\frac{1}{5}\) has the wrong software.
\(\frac{1}{20}\) + \(\frac{1}{5}\)
The fractions have unlike denominators. First, find the Least Common Denominator and rewrite the fractions with the common denominator.
LCD of 5 and 20 is 20
\(\frac{1}{20}\) + \(\frac{4}{20}\) = \(\frac{5}{20}\) = \(\frac{1}{4}\)
Question 12.
Use Structure On Tuesday, the dance team spends \(\frac{1}{8}\) of the practice time trying on uniforms and \(\frac{1}{6}\) of the time choosing music. They spend the remaining time dancing.
- What fraction of practice time do they spend dancing?
- Explain how you found your answer.
Answer:
Given,
On Tuesday, the dance team spends \(\frac{1}{8}\) of the practice time trying on uniforms and \(\frac{1}{6}\) of the time choosing music.
1 – \(\frac{1}{8}\) = \(\frac{7}{8}\)
\(\frac{7}{8}\) – \(\frac{1}{6}\)
The fractions have unlike denominators. First, find the Least Common Denominator and rewrite the fractions with the common denominator.
LCD of 8 and 6 is 24.
\(\frac{21}{24}\) – \(\frac{4}{24}\) = \(\frac{17}{24}\)
Thus they spend \(\frac{17}{24}\) of practice time for dancing.
Find the sum or difference.
Question 13.
\(\frac{2}{5}\) – \(\frac{1}{10}\)
Answer:
\(\frac{2}{5}\) – \(\frac{1}{10}\)
The fractions have unlike denominators. First, find the Least Common Denominator and rewrite the fractions with the common denominator.
LCD of 5 and 10 is 10.
\(\frac{4}{10}\) – \(\frac{1}{10}\) = \(\frac{3}{10}\)
Question 14.
\(\frac{3}{4}\) – \(\frac{1}{8}\)
Answer:
\(\frac{3}{4}\) – \(\frac{1}{8}\)
The fractions have unlike denominators. First, find the Least Common Denominator and rewrite the fractions with the common denominator.
LCD of 4 and 8 is 8.
\(\frac{6}{8}\) – \(\frac{1}{8}\) = \(\frac{5}{8}\)
Question 15.
\(\frac{1}{3}\) + \(\frac{5}{12}\)
Answer:
\(\frac{1}{3}\) + \(\frac{5}{12}\)
The fractions have unlike denominators. First, find the Least Common Denominator and rewrite the fractions with the common denominator.
LCD of 3 and 12 is 12.
\(\frac{4}{12}\) + \(\frac{5}{12}\) = \(\frac{9}{12}\)
Question 16.
\(\frac{1}{6}\) + \(\frac{3}{4}\)
Answer:
\(\frac{1}{6}\) + \(\frac{3}{4}\)
The fractions have unlike denominators. First, find the Least Common Denominator and rewrite the fractions with the common denominator.
\(\frac{1}{6}\) + \(\frac{3}{4}\)
LCD of 4 and 6 is 12.
\(\frac{2}{12}\) + \(\frac{9}{12}\) = \(\frac{11}{12}\)
Question 17.
Attend to Precision Malcolm completes \(\frac{1}{5}\) of his new video game. After one week, he completes another \(\frac{1}{10}\) of the game. After two weeks, he completes another \(\frac{1}{2}\) of the game. How much of the game does he complete? Model with an expression and find the sum.
Answer:
Given,
Malcolm completes \(\frac{1}{5}\) of his new video game.
After one week, he completes another \(\frac{1}{10}\) of the game.
After two weeks, he completes another \(\frac{1}{2}\) of the game.
\(\frac{1}{5}\) + \(\frac{1}{10}\) + \(\frac{1}{2}\)
LCD of 5, 10, 2 is 10
\(\frac{2}{10}\) + \(\frac{1}{10}\) + \(\frac{5}{10}\) = \(\frac{8}{10}\) = \(\frac{4}{5}\)
Thus he completes \(\frac{4}{5}\) of the game.