Learn the simple steps to dive numbers on a number line. The number line is a straight line having numbers at equal intervals. The division is nothing but the continuous process of subtraction. This page contains the definition of the number line, division, how to divide on a number line with the detailed process, and solved example questions on it.
Do Check More Articles:
- Addition on a Number Line
- Expressing Numbers on the Number Line
- Representing Fractions On Number Line
- Representation of Integers on a Number Line
What is a Number Line?
A number line is defined as the straight line having numbers at equal intervals or segments along with its length. It can be extended infinitely in any direction. It is represented in a horizontal direction with two arrows on both sides. One can perform all four arithmetic operations like addition subtraction, multiplication, and division using the number line. Let us discuss the method of dividing numbers on a number line in the following sections.
How do you Divide on a Number Line?
In general, we perform division using long division or multiplication but here we are learning to find the division of numbers on a number line. Check out the instructions and detailed process and get the result.
- Draw a number line and it must have the dividend and divisor.
- Subtract the divisor number from the dividend.
- Repeat the subtraction process until you get zero or the number less than the divisor.
- The number of times divisor subtracted is called the quotient.
- Subtraction of the last number and divisor is called the remainder.
Also, check:
- Word Problems on Division by 2 Digit Number
- Dividend Divisor Quotient And Remainder
- Shortcut Method of Division
Division using a Number Line Examples
Example 1:
Divide 56 ÷ 8.
Solution:
8 is subtracted repeatedly from 56 using the number line
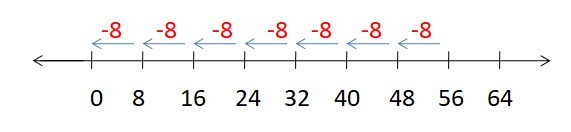
When 8 is subtracted 7 times from 56 in the number line, then we get the remainder zero.
Thus, 8 is subtracted from 56, 7 times.
So, 56 divided by 8 is equal to 7 with a remainder of zero.
Hence, 56 ÷ 8 = 7, 7 is the quotient.
Example 2:
Divide 70 ÷ 7.
Solution:
7 is subtracted repeatedly from 70 using the number line

When 7 is subtracted 10 times from 70 in the number line, then we get the remainder zero.
Thus, 7 is subtracted from 70, 10 times.
So, 70 divided by 7 is equal to 10 with a remainder of zero.
Hence, 70 ÷ 7 = 10, 10 is the quotient.
Example 3:
Divide 16 ÷ 4.
Solution:
4 is subtracted repeatedly from 16 using the number line
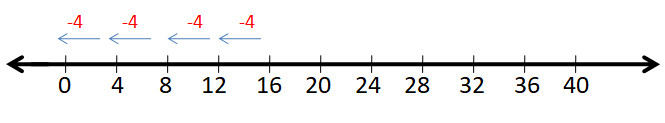
When 4 is subtracted 4 times from 16 in the number line, then we get the remainder zero.
Thus, 4 is subtracted from 16, 4 times.
So, 16 divided by 4 is equal to 4 with a remainder of zero.
Hence, 16 ÷ 4 = 4, 4 is the quotient.
FAQs on Dividing a Number Line
1. Is division possible on a number line?
Yes, it is possible to represent the division on a number line.
2. What are symbols for division?
The different symbols used for the division are ÷ or /.
3. What is the short division method?
It is also called the bus stop method. Here, the steps are performed mentally and the division steps are breakdown into easier steps.
