Students looking for the Bridges in Mathematics Grade 5 Student Book Answer Key Unit 5 Module 4 can find a better approach to solve the problems.
Bridges in Mathematics Grade 5 Student Book Answer Key Unit 5 Module 4
Bridges in Mathematics Grade 5 Student Book Unit 5 Module 4 Session 1 Answer Key
Grouping or Sharing?
Question 1.
Decide whether each of the story problems below involves the sharing or the grouping interpretation of division. Circle your choice. You don’t need to solve the problems, but it may help to think about whether the answer will mean how many items are in each group or how many groups can be made.
a. Frank picked 12 flowers. He divided the flowers evenly between 3 vases. How many flowers did he put in each vase?

Sharing
Grouping
Answer: Sharing
Sharing happens where we know the number being divided and the number of groups. Grouping happens where we know the number being divided and the size of each group. Here we know the number being divided.
b. Erica had 20 baseball cards. She put them up on her bulletin board in rows containing 5 cards. How many rows was she able to make?

Sharing
Grouping
Answer: Grouping
Sharing happens where we know the number being divided and the number of groups. Grouping happens where we know the number being divided and the size of each group. Here we are finding the size.
c. Darius and his dad made 28 cupcakes for the bake sale. They put 7 cupcakes on each plate. How many plates of cupcakes were they able to make?
Sharing
Grouping
Answer: Grouping
Sharing happens where we know the number being divided and the number of groups. Grouping happens where we know the number being divided and the size of each group. Here we are finding the size.
d. Kiara and her sister are collecting pennies. They have 120 pennies so far. They put their pennies into stacks of 10. How many stacks were they able to make?

Sharing
Grouping
Answer: sharing
Sharing happens where we know the number being divided and the number of groups. Grouping happens where we know the number being divided and the size of each group. Here we know the number being divided.
e. Carlos has 15 toy cars. He wants to share them with 2 of his friends so all three boys have the same number. How many cars will each kid get?

Sharing
Grouping
Answer: Sharing
Sharing happens where we know the number being divided and the number of groups. Grouping happens where we know the number being divided and the size of each group. Here we know the number being divided.
f. Jade and her sister made $5.00 doing chores for their mom. They split the money evenly between themselves. How much money did each girl get?

Sharing
Grouping
Answer: Sharing
Sharing happens where we know the number being divided and the number of groups. Grouping happens where we know the number being divided and the size of each group. Here we know the number being divided.
Question 2.
Read each story problem. Then:
- Write an equation (including the answer) for the problem.
- Fill in the bubble to show whether the answer means the size of each group or the number of groups.
a. Mai and her mother made 24 invitations to Mai’s birthday party. They put the invitations into stacks of 4. How many stacks did they make?
Equation: ____________
The answer means:
![]() the size of each group (for example, the number of items each person got)
the size of each group (for example, the number of items each person got)
![]() the number of groups
the number of groups
Answer: the number of groups
Number of invitations = 24
number of invitations in one stack = 4
total number of stacks = 24 / 4 = 6
b. Troy and his mom got a case of bottled water for the soccer game. They divided the 24 bottles evenly among the 12 boys on the team. How many bottles of water did each boy get?
Equation:
The answer means:
![]() the size of each group (for example, the number of items each person got)
the size of each group (for example, the number of items each person got)
![]() the number of groups
the number of groups
Answer: the size of each group (for example, the number of items each person got)
total number of boys = 12
total number of bottles = 24
therefore, total number of bottles each boy get = 24 / 12 =2
Question 3.
Choose one of the expressions below and circle your choice. Write a sharing story problem and a grouping story problem about the same expression.
18 ÷ 6
60 ÷ 12
108 ÷ 4
400 ÷ 25
Answer:
Expression taken : 18 ÷ 6
Sharing story problem :
Roy and his mom got a case of bottled water for the soccer game. They divided the 18 bottles evenly among the 6 boys on the team. How many bottles of water did each boy get?
Grouping story problem:
Mai and her mother made 18 invitations to Mai’s birthday party. They put the invitations into stacks of 6. How many stacks did they make?
Skills Review 1
Question 1.
Use the standard algorithm to solve the two multiplication problems below.

Answer:

Question 2.
Fill in the ratio table for 32. Then use the information to solve the long division problem. You can add more information to the ratio table if you like.

Answer: 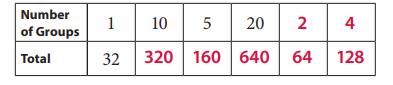
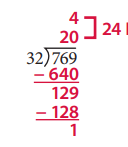
Question 3.
Add. Show your work.
3.80 + 17.46 = ____________
Answer: 21.26
3.80 + 17.46 = 21.26
Question 4.
Add. Show your work.
\(\frac{2}{5}\) + 3\(\frac{3}{4}\) = _______________
Answer: 4\(\frac{3}{20}\)
\(\frac{2}{5}\) + 3\(\frac{3}{4}\) = \(\frac{2}{5}\) + \(\frac{15}{4}\)
= \(\frac{8}{20}\) + \(\frac{75}{20}\)
= \(\frac{83}{20}\)
= 4\(\frac{3}{20}\)
Question 5.
Multiply. Show your work. Simplify your answer to lowest terms.
\(\frac{3}{4}\) × \(\frac{4}{6}\) = _______________
Answer: \(\frac{1}{2}\)
\(\frac{3}{4}\) x \(\frac{4}{6}\) = \(\frac{12}{24}\)
= \(\frac{1}{2}\)
Question 6.
Multiply. Show your work. Express your answer as a mixed number.
4 × \(\frac{3}{5}\) = _______________
Answer: \(\frac{12}{5}\) = 2\(\frac{2}{5}\)
Bridges in Mathematics Grade 5 Student Book Unit 5 Module 4 Session 2 Answer Key
Skills Review 2
Question 1.
Subtract. Show your work.
18.03 – 4.59 = ______________
Answer: 13.44
18.03 – 4.59 = 13.44
Question 2.
Add. Show your work.
4\(\frac{2}{3}\) + 5\(\frac{3}{4}\) = ______________
Answer: 10\(\frac{5}{12}\)
4\(\frac{2}{3}\) + 5\(\frac{3}{4}\) = \(\frac{14}{3}\) + \(\frac{23}{4}\)
= \(\frac{56}{12}\) + \(\frac{69}{12}\)
= \(\frac{56+69}{12}\)
= \(\frac{125}{12}\)
= 10\(\frac{5}{12}\)
Question 3.
Use the array to model and solve this multiplication problem.
\(\frac{3}{4}\) × \(\frac{5}{6}\) = ______________
Answer: \(\frac{15}{24}\) = \(\frac{5}{8}\)
\(\frac{3}{4}\) × \(\frac{5}{6}\) = \(\frac{15}{24}\) = \(\frac{5}{8}\)
Question 4.
Fill in the ratio table for 27. Then use the information to solve the division problem.

Answer: 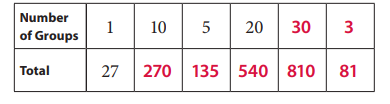
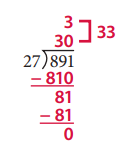
Question 5.
The fifth graders are painting the bookshelves in their classroom. It takes \(\frac{3}{4}\) of a quart of paint to paint each bookshelf. There are 8 bookshelves in the room. How many quarts of paint will the kids need to paint all 8 bookshelves?
- Write an expression to represent this problem.
- Solve the problem. Show your work with labeled visual models, numbers, or words.
Expression: _______________
Answer: 8 x \(\frac{3}{4}\)
Total number of bookshelves = 8
It takes \(\frac{3}{4}\) of a quart of paint to paint each bookshelf.
Therefore, the quarts of paint will the kids need to paint all 8 bookshelves = total shelves x paint for each shelf
= 8 x \(\frac{3}{4}\)
Bridges in Mathematics Grade 5 Student Book Unit 5 Module 4 Session 3 Answer Key
Do-It-Yourself Story Problems
Question 1.
Solve each of the story problems below. For each problem:
- Choose and circle one of the numbers in parentheses, depending on how challenging you want the problem to be.
- Write an expression to represent your problem.
- Use numbers, labeled visual models, or words to solve the problem and explain your strategy.
- Complete the sentence below with your solution to the problem
a. It takes (\(\frac{1}{2}\), \(\frac{1}{4}\), \(\frac{3}{4}\), \(\frac{3}{8}\)) of a cup of sugar to make a batch of cookies. I have 5 cups of sugar. How many batches of cookies can I make?
Expression: _______________
I can make ______________ batches of cookies.
Answer:
Expression taken : \(\frac{1}{2}\)
total number of sugar cups = 5
number of cookies make = 5 / \(\frac{1}{2}\),
= 5 x 2 =10
I can make 10 batches of cookies.
b. The road-repair crew can fix \(\frac{1}{2}\) a mile of road per day. How many days will it take them to fix a stretch of road that is (4 miles, 5 miles, 6\(\frac{1}{2}\) miles, 8\(\frac{3}{4}\) miles)?
Expression: _______________

I will take ______________ days to fix the road.
Answer:
Expression: 4 miles
road-repair crew can fix \(\frac{1}{2}\) a mile of road per day
number of days = 4 / \(\frac{1}{2}\)
= 4 x 2 = 8 days
I will take 8 days to fix the road.
c. How many (\(\frac{1}{2}\) cup, \(\frac{1}{3}\) cup, \(\frac{1}{4}\) cup, \(\frac{2}{3}\) cup) servings are there in a quart of ice cream? There are 4 cups in a quart.
Expression: ______________

There are ______________ servings in a quart of ice cream.
Answer:
Expression : \(\frac{1}{2}[/latex
total number of cups = 4
number of servings that are there ina quart of ice cream = 4 / [latex]\frac{1}{2}[/latex
= 4 x 2 = 8
There are 8 servings in a quart of ice cream.
d. Little Snail is going to visit his friend over at the next pond, 3 miles away. He can crawl ([latex]\frac{1}{2}\), \(\frac{1}{3}\), \(\frac{1}{4}\), \(\frac{3}{4}\), \(\frac{2}{3}\)) of a mile per day. How many days will it take him to get there?
Expression: ______________

It will take _____________ days to get there.
Answer:
Expression : (\(\frac{1}{2}\)
number of miles = 3
number of days = 3 / (\(\frac{1}{2}\)
= 3 x 2 = 6 days
It will take 6 days to get there.
Question 2.
Choose one of the expressions below and circle your choice. Write a story problem about the expression you circled. Then solve your own problem using a fractional visual model.
10 ÷ \(\frac{1}{2}\) =
12 ÷ \(\frac{1}{3}\) =
20 ÷ \(\frac{1}{4}\) =
24 ÷ \(\frac{2}{3}\) =
My story problem: _____________
My work: _____________
The answer to my problem is _____________
Answer:
Expression: 10 ÷ \(\frac{1}{2}\)
My story problem: The road-repair crew can fix \(\frac{1}{2}\) a mile of road per day. How many days will it take them to fix a stretch of road that is 10 miles?
My work :
number of miles = 10
road-repair crew can fix \(\frac{1}{2}\) a mile of road per day
therefore, number of days = 10 / \(\frac{1}{2}\)
= 10 ÷ \(\frac{1}{2}\) = 10 x 2 = 20
The answer to my problem is : 20
Skills Review 3
Question 1.
Multiply. Show your work.
23.69 × 14 = ________________
Answer: 331.66
23.69 x 14 = 331.66
Question 2.
Subtract. Show your work.
\(\frac{7}{8}\) – \(\frac{5}{6}\) = _______________
Answer: \(\frac{1}{24}\)
\(\frac{7}{8}\) – \(\frac{5}{6}\) = \(\frac{42}{48}\) – \(\frac{40}{48}\)
= \(\frac{2}{48}\)
= \(\frac{1}{24}\)
Question 3.
Use the standard algorithm to multiply these numbers.
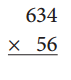
Answer: 35504
634
x 56
———-
3804
+31700
———-
35504
Question 4.
Round 129.392 to the nearest:

Answer: 
Question 5.
There was \(\frac{1}{2}\) of a cake left over from Hannah’s birthday party. When she and her sister came home from school the next day, they ate 3 of the leftover cake for a snack. How much of the whole cake did the girls have for their snack?
- Write an expression to represent this problem.
- Solve the problem. Show your work with labeled visual models, numbers, or words.
Expression: ______________
Answer:
left over cake = \(\frac{1}{2}\)
Expression : \(\frac{1}{2}\) / 3
Bridges in Mathematics Grade 5 Student Book Unit 5 Module 4 Session 4 Answer Key
Skills Review 4
Question 1.
Divide. Show your work.
$225.40 ÷ 5 = _______________
Answer: $45.08
$225.40 ÷ 5 = $45.08
Question 2.
Subtract. Show your work.
\(\frac{8}{5}\) – \(\frac{2}{3}\) = _______________
Answer: \(\frac{14}{15}\)
\(\frac{8}{5}\) – \(\frac{2}{3}\) = \(\frac{24}{15}\) – \(\frac{10}{15}\)
= \(\frac{14}{15}\)
Question 3.
Fill in the ratio table for 38. Then use the information to solve the long division problem.

Answer: 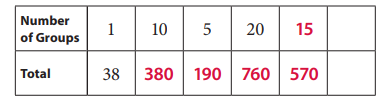
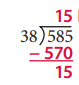
Question 4.
Choose the best estimate for this combination.
\(\frac{2}{3}\) – \(\frac{1}{4}\) = _______________
![]() less than \(\frac{1}{2}\)
less than \(\frac{1}{2}\)
![]() between \(\frac{1}{2}\) and \(\frac{3}{4}\)
between \(\frac{1}{2}\) and \(\frac{3}{4}\)
![]() between \(\frac{5}{6}\) and 1
between \(\frac{5}{6}\) and 1
![]() more than 1
more than 1
Why is this the best estimate?
Answer: between \(\frac{5}{6}\) and 1
\(\frac{2}{3}\) – \(\frac{1}{4}\) = \(\frac{8}{12}\) – \(\frac{3}{12}\)
= \(\frac{5}{12}\)
\(\frac{5}{12}\) is between \(\frac{5}{6}\) and 1
Question 5.
Write a story problem to represent the expression below. Then solve your problem. Show your work with labeled models, numbers, or words, and write the answer on the line provided.
6 ÷ \(\frac{1}{3}\) = ________________
My Story Problem: _______________
My work:
Answer:
Expression: 6 ÷ \(\frac{1}{3}\)
My story problem: The road-repair crew can fix \(\frac{1}{3}\) a mile of road per day. How many days will it take them to fix a stretch of road that is 6 miles?
My work :
number of miles = 6
road-repair crew can fix \(\frac{1}{3}\) a mile of road per day
therefore, number of days = 6 / \(\frac{1}{3}\)
= 6 ÷ \(\frac{1}{3}\) = 6 x 3 = 18
Bridges in Mathematics Grade 5 Student Book Unit 5 Module 4 Session 5 Answer Key
More Do-It-Yourself Story Problems
Question 1.
Solve each of the story problems below. For each problem:
- Choose and circle one of the numbers in parentheses.
- Write an expression to represent your problem.
- Use numbers, labeled visual model, or words to solve the problem.
- Complete the sentence below with your solution to the problem
a. (Two, three, four) dinner guests shared (\(\frac{1}{2}\), \(\frac{1}{3}\), \(\frac{2}{3}\), \(\frac{3}{4}\)) of a pan of cornbread. What fraction of the pan of cornbread did each guest get?
Each guest got ____________ pan of cornbread.
Answer:
number of guests = 2
number of pans of corn bread shared = \(\frac{1}{2}\)
each guest got = \(\frac{1}{2}\) / 2 = \(\frac{1}{4}\)
Each guest got \(\frac{1}{4}\) pan of cornbread.
b. Five cousins shared (\(\frac{1}{2}\), \(\frac{1}{3}\), \(\frac{1}{4}\), \(\frac{3}{4}\)) of a birthday cake. What fraction of the cake did each cousin get?
Expression: ________________
Each cousin got _______________ of the birthday cake.
Answer:
expression: \(\frac{1}{2}\)
number of cousins = 5
each cousin got = \(\frac{1}{2}\) / 5 = \(\frac{1}{10}\)
Each cousin got \(\frac{1}{10}\) of the birthday cake.
c. Sara had (\(\frac{1}{2}\), \(\frac{1}{3}\), \(\frac{2}{3}\)) of a cup of grated cheese. She divided it equally between 4 salads. What fraction of a cup of cheese did each salad get?
Expression: ________________

There was _______________ a cup on each salad.
Answer:
expression: \(\frac{1}{2}\)
number of salads = 4
There was \(\frac{1}{8}[/latex] a cup on each salad.
d. Mr. Brown had [latex]\frac{1}{8}\) of a pack of paper. He divided the pack equally among equally among 3 students. What fraction of the pack of paper did each student get?
Expression: ________________
Each student got ________________ a pack of paper.
Answer:
Expression: \(\frac{1}{8}\) / 3
Each student got \(\frac{3}{8}\) a pack of paper
e. There were 504 sheets of paper in the whole pack. How many sheets of paper did each of the 3 students get?
Expression: ________________
Each student got ________________ sheets of paper.
Answer:
Expression: 504 / 3
total number of sheets = 504
total number of students = 3
each student got = 504 / 3 = 168
Each student got 168 sheets of paper.
Question 2.
Choose one of the expressions below and circle your choice. Write a story problem about the expression you circled. Then solve your own problem.
\(\frac{1}{2}\) ÷ 2 =
\(\frac{1}{2}\) ÷ 6 =
\(\frac{1}{3}\) ÷ 4 =
\(\frac{1}{8}\) ÷ 4 =
My story problem is: ________________
My work: ________________
The answer to my problem is: ________________
Answer:
Expression: \(\frac{1}{2}\) ÷ 2
My story problem: There are \(\frac{1}{2}\) of fruits. How to divide this to 2 people?
My work :
number of fruits = \(\frac{1}{2}\)
number of people = 2
division = \(\frac{1}{2}\) ÷ 2 = \(\frac{2}{2}\) = 1
Skills Review 5
Question 1.
Subtract. Show your work.
234.02 – 87.46 = ________________
Answer: 146.56
234.02 – 87.46 = 146.56
Question 2.
Subtract. Show your work.
7\(\frac{2}{3}\) – 5\(\frac{3}{4}\) = ______________
Answer: 1\(\frac{11}{12}\)
7\(\frac{2}{3}\) – 5\(\frac{3}{4}\) = \(\frac{23}{3}\) – \(\frac{23}{4}\)
= \(\frac{92}{12}\) – \(\frac{69}{12}\)
= \(\frac{23}{12}\)
= 1\(\frac{11}{12}\)
Question 3.
Using the grid below, create an array to model and solve this problem.
\(\frac{2}{5}\) × \(\frac{3}{4}\) = ______________

Answer:
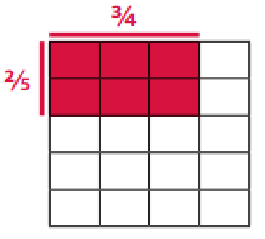
\(\frac{2}{5}\) × \(\frac{3}{4}\) = \(\frac{6}{20}\)
= \(\frac{3}{10}\)
Question 4.
Add. Show your work.
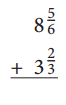
Answer:
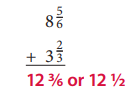
Question 5.
Write a story problem to represent the expression below. Then solve your problem. Show your work with labeled models, numbers, or words, and write the answer on the line provided.
\(\frac{1}{2}\) ÷ 3 = ________________
My Story Problem: ________________
My work: ________________
Answer:
Expression: \(\frac{1}{2}\) ÷ 3
My story problem: There are \(\frac{1}{2}\) of fruits. How to divide this to 3 people?
My work :
number of fruits = \(\frac{1}{2}\)
number of people = 3
division= \(\frac{1}{2}\) ÷ 3 = \(\frac{3}{2}\) = 1.5
Bridges in Mathematics Grade 5 Student Book Unit 5 Module 4 Session 6 Answer Key
Fraction Estimate & Check
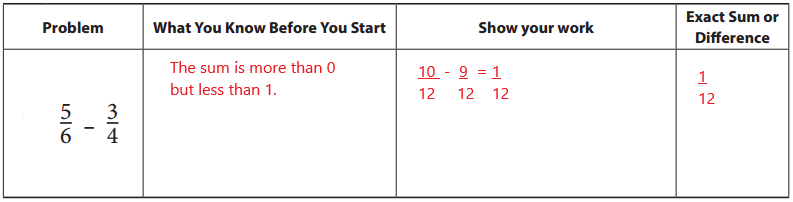
Before you solve each problem, look carefully at the fractions and write what you know about the sum or difference. Then find the exact sum or difference. Show all your work. If your answer is greater than 1, write it as a mixed number, not an improper fraction.
ex:
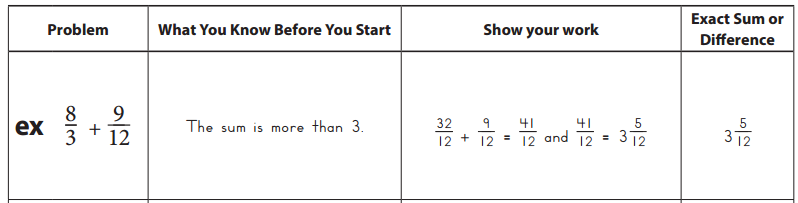
Question 1.
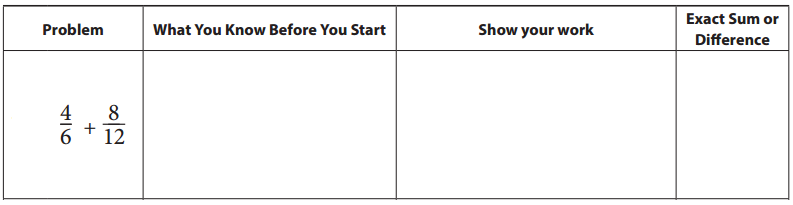
Answer: 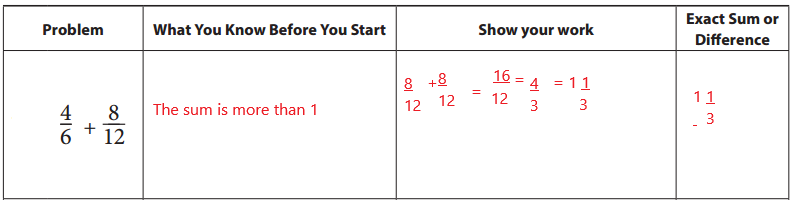
Question 2.
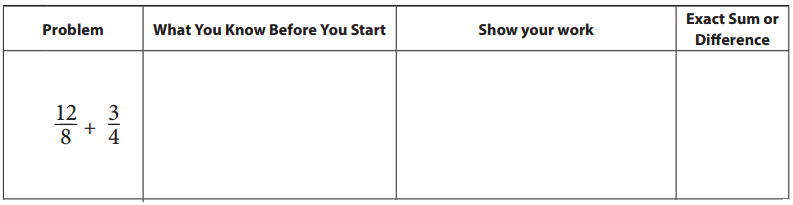
Answer: 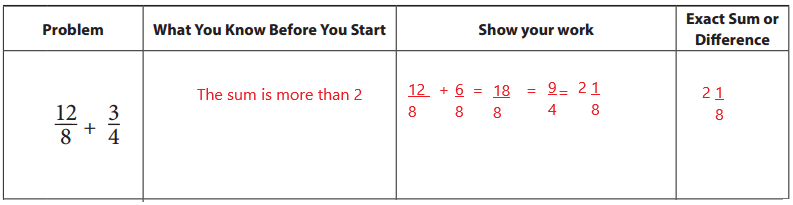
Question 3.
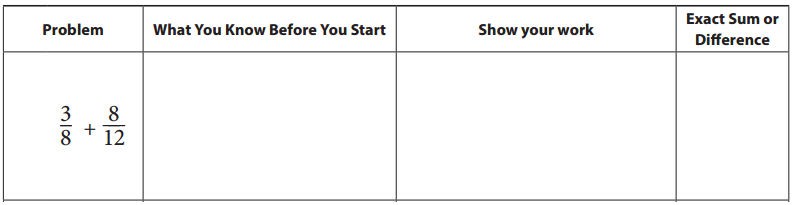
Answer: 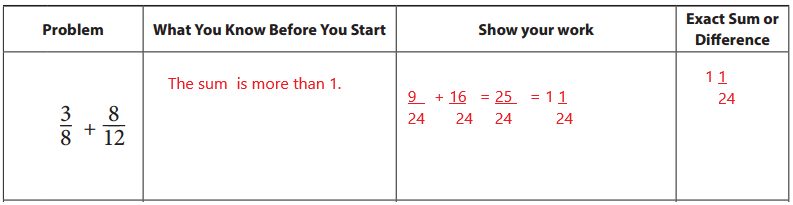
Question 4.
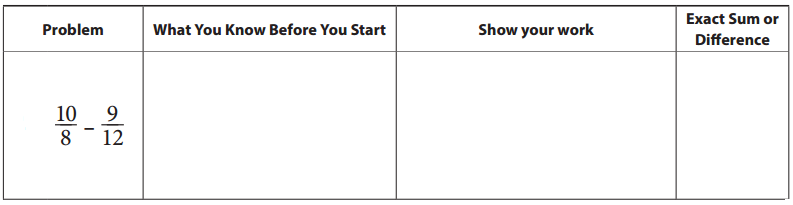
Answer: 
Question 5.
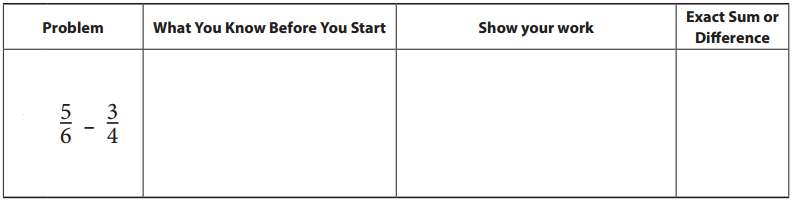
Answer: