Students looking for the Bridges in Mathematics Grade 5 Student Book Answer Key Unit 5 Module 3 can find a better approach to solve the problems.
Bridges in Mathematics Grade 5 Student Book Answer Key Unit 5 Module 3
Bridges in Mathematics Grade 5 Student Book Unit 5 Module 3 Session 1 Answer Key
Picturing Fraction Multiplication
Question 1.
Each of the pictures below shows the results of multiplying one fraction by another. Label each of the shaded regions with its dimensions and area. Then write a multiplication equation to match.
ex:
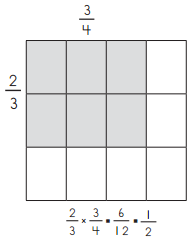
a.

Answer: 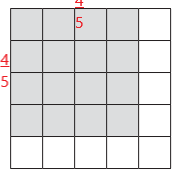
\(\frac{4}{5}\) x \(\frac{4}{5}\) = \(\frac{16}{25}\)
b.
Answer: 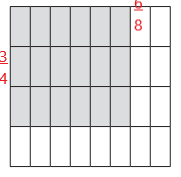
\(\frac{3}{4}\) x \(\frac{6}{8}\) = \(\frac{18}{32}\) = \(\frac{9}{16}\)
c.
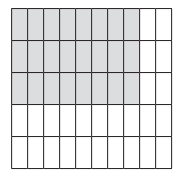
Answer: 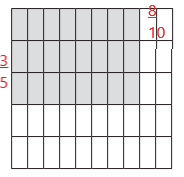
\(\frac{3}{5}\) x \(\frac{8}{10}\) = \(\frac{24}{50}\) = \(\frac{12}{25}\)
Question 2.
Pedro is using paper rectangles that are all the same size to make a collage. Each piece is \(\frac{3}{4}\) inch by \(\frac{1}{2}\) inch. What is the area of each piece? Use numbers, words, or pictures to solve the problem. Show your work.
Each piece had an area of ______________ square inch.
Answer:
Pedro is using paper rectangles that are all the same size to make a collage.
Each piece is \(\frac{3}{4}\) inch by \(\frac{1}{2}\) inch.
Area = \(\frac{3}{4}\) x \(\frac{1}{2}\)
Area = \(\frac{3}{8}\)
Bridges in Mathematics Grade 5 Student Book Unit 5 Module 3 Session 2 Answer Key
Modeling Fraction Multiplication
Question 1.
Circle the picture that best represents each problem.
a. \(\frac{1}{2}\) × \(\frac{1}{2}\) = _______________

Answer:

\(\frac{1}{2}\) × \(\frac{1}{2}\) = \(\frac{1}{4}\)
b. \(\frac{2}{3}\) × \(\frac{1}{4}\) = _______________

Answer: 
\(\frac{2}{3}\) × \(\frac{1}{4}\) = \(\frac{2}{12}\) = \(\frac{1}{6}\)
Question 2.
Use the squares to model each combination and find the products. You will need to divide the sides of each square in order to represent each fraction as a dimension.
a. \(\frac{4}{5}\) × \(\frac{5}{6}\) = _______________

Answer: 
\(\frac{4}{5}\) × \(\frac{5}{6}\) = \(\frac{20}{30}\)
b. \(\frac{7}{8}\) × \(\frac{2}{5}\) = _______________

Answer: 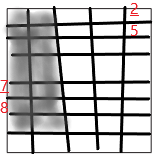
\(\frac{7}{8}\) × \(\frac{2}{5}\) = \(\frac{14}{40}\) = \(\frac{7}{20}\)
c. \(\frac{1}{4}\) × \(\frac{2}{6}\) = _______________

Answer: 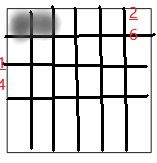
\(\frac{1}{4}\) × \(\frac{2}{6}\) = \(\frac{2}{24}\) = \(\frac{1}{12}\)
Bridges in Mathematics Grade 5 Student Book Unit 5 Module 3 Session 3 Answer Key
Reasoning About Multiplying with Fractions
Write =, >, or < to make each statement true.
Question 1.
3 × 45 = B
a. B ________ 3
b. B ________ 45
Answer:
3 x 45 = B
3 x 45 = 135
B = 135
a. B > 3
b. B > 45
Question 2.
3 × 1 = C
a. C _________ 3
b. C _________ 1
Answer:
3 x 1 = C
3 x 1 = 3
C = 3
a. C = 3
b. C > 1
Question 3.
\(\frac{3}{4}\) × 1 = A
a. A ________ 1
b. A ________ \(\frac{3}{4}\)
Answer:
\(\frac{3}{4}\) × 1 = A
\(\frac{3}{4}\) × 1 = \(\frac{3}{4}\)
A = \(\frac{3}{4}\)
a. A < 1
b. A = \(\frac{3}{4}\)
Question 4.
\(\frac{1}{2}\) × \(\frac{1}{2}\) = P
a. P ________ \(\frac{3}{7}\)
b. P ________ \(\frac{4}{15}\)
c. P ________ 1
Answer:
\(\frac{1}{2}\) × \(\frac{1}{2}\) = P
\(\frac{1}{2}\) × \(\frac{1}{2}\) = \(\frac{1}{4}\)
P = \(\frac{1}{4}\)
a. P < \(\frac{3}{7}\)
b. P < \(\frac{4}{15}\)
c. P > 1
Question 5.
1\(\frac{7}{9}\) x \(\frac{5}{6}\) = Q
a. Q __________ 1\(\frac{7}{9}\)
b. Q __________ \(\frac{5}{6}\)
c. Q __________ 1
Answer:
1\(\frac{7}{9}\) x \(\frac{5}{6}\) = Q
1\(\frac{7}{9}\) x \(\frac{5}{6}\) = \(\frac{16}{9}\) x \(\frac{5}{6}\) = \(\frac{40}{27}\)
Q = \(\frac{40}{27}\)
a. Q > 1\(\frac{7}{9}\)
b. Q < \(\frac{5}{6}\)
c. Q > 1
Question 6.
\(\frac{6}{17}\) × 7 = S
a. S _________ \(\frac{6}{17}\)
b. S _________ 7
c. S _________ 2
Answer:
\(\frac{6}{17}\) × 7 = S
\(\frac{6}{17}\) × 7 = \(\frac{42}{17}\)
S = \(\frac{42}{17}\)
a. S > \(\frac{6}{17}\)
b. S < 7
c. S > 2
Question 7.
Choose the pair of fractions that must have a product less than 1. Then compute the exact product.
2 × \(\frac{7}{8}\)
\(\frac{5}{8}\) × \(\frac{2}{3}\)
1\(\frac{1}{2}\) × 1\(\frac{1}{2}\)
3 × 2\(\frac{2}{3}\)
Answer: The pair of fractions that have a product less than 1 is \(\frac{5}{8}\) × \(\frac{2}{3}\) = \(\frac{5}{12}\)
2 × \(\frac{7}{8}\) = \(\frac{7}{4}\)
\(\frac{5}{8}\) × \(\frac{2}{3}\) = \(\frac{5}{12}\)
1\(\frac{1}{2}\) × 1\(\frac{1}{2}\) = \(\frac{3}{2}\) x \(\frac{3}{2}\) = \(\frac{9}{4}\)
3 × 2\(\frac{2}{3}\) = 3 x \(\frac{8}{3}\) = 3
More Fraction Multiplication
Question 1.
Fill in the chart to solve each of the problems below.
ex:
Multiplication Equation: \(\frac{2}{3}\) × \(\frac{2}{3}\) = \(\frac{4}{9}\)
Labeled Sketch:
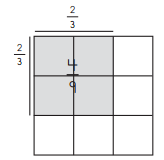
a. Multiplication Equation: \(\frac{2}{3}\) × \(\frac{6}{7}\) =
Labeled Sketch:
Answer: 
\(\frac{2}{3}\) × \(\frac{6}{7}\) = \(\frac{12}{21}\) = \(\frac{4}{7}\)
b. Multiplication Equation: \(\frac{1}{2}\) × \(\frac{4}{6}\) =
Labeled Sketch:
Answer:
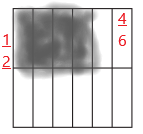
\(\frac{1}{2}\) × \(\frac{4}{6}\) = \(\frac{4}{12}\) = \(\frac{1}{3}\)
c. Multiplication Equation: \(\frac{3}{4}\) × \(\frac{4}{8}\) =
Labeled Sketch:
Answer:
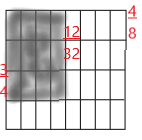
\(\frac{3}{4}\) × \(\frac{4}{8}\) = \(\frac{12}{32}\) = \(\frac{3}{8}\)
Question 2.
Solve each problem.
\(\frac{3}{4}\) × \(\frac{2}{4}\) = _______________
\(\frac{1}{4}\) × \(\frac{3}{6}\) = _______________
\(\frac{5}{6}\) × \(\frac{1}{2}\) = _______________
\(\frac{6}{7}\) × \(\frac{3}{5}\) = _______________
\(\frac{2}{3}\) × \(\frac{4}{5}\) = _______________
\(\frac{6}{8}\) × \(\frac{1}{2}\) = _______________
\(\frac{3}{4}\) × \(\frac{1}{3}\) = _______________
\(\frac{2}{7}\) × \(\frac{2}{4}\) = _______________
Answer:
\(\frac{3}{4}\) × \(\frac{2}{4}\) = \(\frac{6}{16}\) = \(\frac{3}{8}\)
\(\frac{1}{4}\) × \(\frac{3}{6}\) = \(\frac{3}{24}\) = \(\frac{1}{8}\)
\(\frac{5}{6}\) × \(\frac{1}{2}\) = \(\frac{5}{12}\)
\(\frac{6}{7}\) × \(\frac{3}{5}\) = \(\frac{18}{35}\)
\(\frac{2}{3}\) × \(\frac{4}{5}\) = \(\frac{8}{15}\)
\(\frac{6}{8}\) × \(\frac{1}{2}\) = \(\frac{6}{16}\)
\(\frac{3}{4}\) × \(\frac{1}{3}\) = \(\frac{3}{12}\) = \(\frac{1}{4}\)
\(\frac{2}{7}\) × \(\frac{2}{4}\) = \(\frac{4}{28}\) = \(\frac{1}{7}\)
Bridges in Mathematics Grade 5 Student Book Unit 5 Module 3 Session 4 Answer Key
Work Place Instructions 5B Tic-Frac-Toe
Each pair of partners needs:
- 1 Tic-Frac-Toe Record Sheet
- 1 deck of Number Cards, with the 0s and wild cards removed
- 2 colored pencils, in different colors
1. Decide who will be the dealer. The dealer deals out four cards to each player.
2. Player 1 decides which space he wants to claim on the Tic-Frac-Toe Record Sheet. He arranges his four cards to make a fraction-times-a-fraction multiplication problem with a product that fits the description in the desired space.
Two cards are numerators and the other two cards are denominators. For example, with the cards 2, 5, 5, and 8, a player could make \(\frac{2}{5}\) × \(\frac{5}{8}\). Since \(\frac{2}{5}\) × \(\frac{5}{8}\) = \(\frac{1}{4}\), Player 1 can fill any space where the product is less than 1, p < 1. By rearranging the cards to make \(\frac{8}{2}\) × \(\frac{5}{5}\) = 4 instead, Player 1 can fill in any space where the product is greater than 1, p > 1.

3. Player 1 writes the equation in the blank in the desired space with a colored pencil.
4. Player 2 arranges her four cards and uses the other colored pencil to write her equation in a space that describes her product.
5. Players continue, using four new cards on each turn and filling spaces until one player has claimed four spaces in a horizontal, vertical, or diagonal row, and wins the game.
Game Variations
A. Change some of the spaces to read p > 2 for products greater than 2 but less than 3, and p > 3 for products greater than 3.
B. Include the wild cards in the deck. A wild card can be any numeral 1-9.
Answer: Tried the game by changing some of the spaces to read p > 2 for products greater than 2 but less than 3, and p > 3 for products greater than 3. Also, included a wild card of number 7.
Tic-Frac-Toe Moves
In Tic-Frac-Toe, you draw four number cards and arrange them to make two fractions, then multiply them to get a product greater than 1 or a product less than 1.
Question 1.
Bill has the cards 6, 4, 2, and 5.
a. How could he arrange his cards to make two fractions with a product greater than 1?
Answer:
Bill has the cards 6, 4, 2, and 5.
Bill can arrange his cards has \(\frac{4}{2}\) × \(\frac{6}{5}\).
b. What would his product be? Write and solve an equation to show.
Answer:
Since \(\frac{4}{2}\) × \(\frac{6}{5}\)= \(\frac{12}{5}\) = 2\(\frac{2}{5}\) which is greater than 1.
c. How could he arrange his cards to make a product less than 1?
Answer:
Bill has the cards 6, 4, 2, and 5.
Bill can arrange his cards has \(\frac{6}{4}\) × \(\frac{2}{5}\).
d. What would his product be? Write and solve an equation to show.
Answer:
Since \(\frac{6}{4}\) × \(\frac{2}{5}\)= \(\frac{3}{5}\) which is less than 1.
Question 2.
Jeremiah has the cards 3, 9, 4, and 1.
a. How could he arrange his cards to make two fractions with a product greater than 1?
Answer:
Jeremiah has the cards 3, 9, 4, and 1
Jeremiah can arrange his cards has \(\frac{9}{3}\) × \(\frac{4}{1}\).
b. What would his product be? Write and solve an equation to show.
Answer:
Since \(\frac{9}{3}\) × \(\frac{4}{1}\)= \(\frac{12}{1}\) = 12 which is greater than 1.
c. How could he arrange his cards to make a product less than 1?
Answer:
Jeremiah has the cards 3, 9, 4, and 1
Jeremiah can arrange his cards has \(\frac{3}{9}\) × \(\frac{1}{4}\).
d. What would his product be? Write and solve an equation to show.
Answer:
Since \(\frac{3}{9}\) × \(\frac{1}{4}\)= \(\frac{1}{12}\) which is less than 1.
Question 3.
Find the products.
\(\frac{4}{7}\) × \(\frac{1}{3}\) = ________________
\(\frac{5}{6}\) × \(\frac{3}{5}\) = ________________
\(\frac{4}{3}\) × \(\frac{3}{4}\) = ________________
\(\frac{3}{7}\) × \(\frac{7}{5}\) = ________________
Answer:
\(\frac{4}{7}\) × \(\frac{1}{3}\) = \(\frac{4}{21}\)
\(\frac{5}{6}\) × \(\frac{3}{5}\) = \(\frac{15}{30}\) = \(\frac{1}{2}\)
\(\frac{4}{3}\) × \(\frac{3}{4}\) = \(\frac{12}{12}\) = 1
\(\frac{3}{7}\) × \(\frac{7}{5}\) = \(\frac{21}{35}\) = \(\frac{3}{5}\)