Practicing the Bridges in Mathematics Grade 4 Student Book Answer Key Unit 1 Module 2 will help students analyze their level of preparation.
Bridges in Mathematics Grade 4 Student Book Answer Key Unit 1 Module 2
Bridges in Mathematics Grade 4 Student Book Unit 1 Module 2 Session 1 Answer Key
Arranging School Supplies
Mrs. Carter is organizing some of her school supplies that came in square boxes. She is trying to figure out the best way to arrange them. She knows she wants everything to be arranged in a single layer as a rectangle, but she is not sure how to arrange the boxes to make the rectangles. Can you help Mrs. Carter? Solve each problem below. Show your work using numbers, sketches, or words.
Question 1.
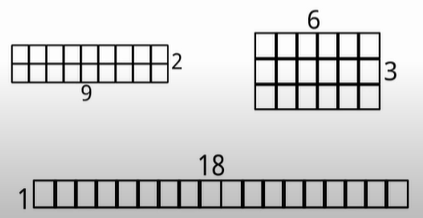
Mrs. Carter has 18 square boxes of tacks.
a. How many different rectangles can she make with the 18 boxes of tacks? What are the dimensions of each of the different rectangles?
Answer:
Three different rectangles. 1 × 18, 2 × 9, and 3 × 6
Explanation:
Given,
No of square boxes of tacks = 18
there are three different rectangles she can make with the 18 boxes of tacks.
The dimensions of each of the different rectangles are 1 × 18, 2 × 9, and 3 × 6
b. How do you know that you found all of the possible rectangles?
Answer:
By using the factors of 18 we can find all the possible rectangles.
Explanation:
No of square boxes of tacks = 18
let us find the factors of 18
3 × 6 = 18
2 × 9 = 18
1 × 18 = 18
By using these factors we can write the dimensions of each of the different rectangles.
Question 2.
Mrs. Carter has 24 square boxes of paperclips. How many different rectangles can she make with the 24 boxes of paperclips? What are the dimensions of each of the different rectangles?
Answer:
There are 4 different rectangles. Their dimensions are 1 × 24, 2 × 12, 3 × 8, and 4 × 6.
Explanation:
Given,
No of square boxes = 24
We need to find out How many different rectangles can she make with the 24 boxes of paperclips?
Now find out the factors of 24
1 × 24 = 24
2 × 12 = 24
3 × 8 = 24
and 4 × 6 = 24
hence the dimensions of each of the different rectangles are 1 × 24, 2 × 12, 3 × 8, and 4 × 6.
a. Mrs. Carter is out of storage space, so she is going to keep her paperclip boxes on the windowsill. What are the dimensions of the rectangle you think Mrs. Carter should use? Explain your thinking.
Answer:
Mrs. Carter should use 1 × 24. The dimensions of the rectangle Mrs. Carter should use is 1 × 24.
Explanation:
Because these rectangles have the same area, so she should use the largest perimeter.
Bridges in Mathematics Grade 4 Student Book Unit 1 Module 2 Session 2 Answer Key
Thinking About Factors
Instructions
Join another pair of students and use your posters from the last session as you discuss and answer the following questions. Refer to your posters to help explain your thinking.
Question 1.
Why do some posters have only one rectangle while others have two or more rectangles?
Answer:
Some posters have only one rectangle while others have two or more rectangles because of the factors of the given posters.
Explanation:
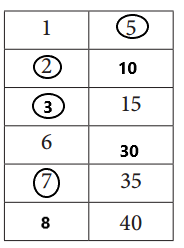
Question 2.
What do all of the posters with even numbers have in common?
Answer:
These even numbers can be divided into two equal groups or pairs and are exactly divisible by 2.
Explanation:
These even numbers have in common is they can be divided into two equal groups or pairs and are exactly divisible by 2.
Question 3.
Some of the arrays are rectangles and some of the arrays are squares. Why is that?
Answer:
Yes, Some of the arrays are rectangles and some of the arrays are squares.
Explanation:
When an array has a different number of rows and a different number of columns it creates a rectangle. When an array has the same number of rows and columns, it creates a square.
Recording Factors
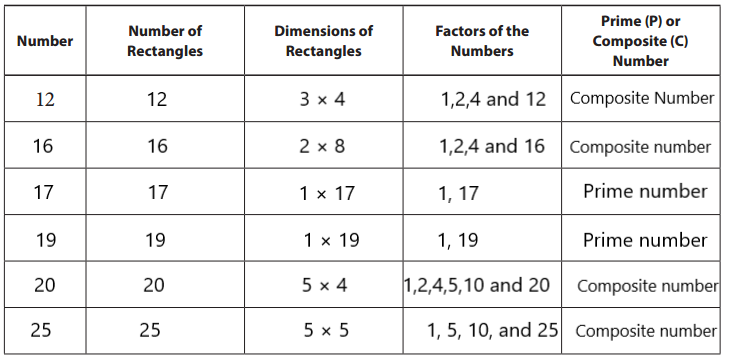
Question 1.
Start by filling in the row for 12. Then write the products from the posters you talked about today in your group in the Number column and fill out the rows for those numbers.
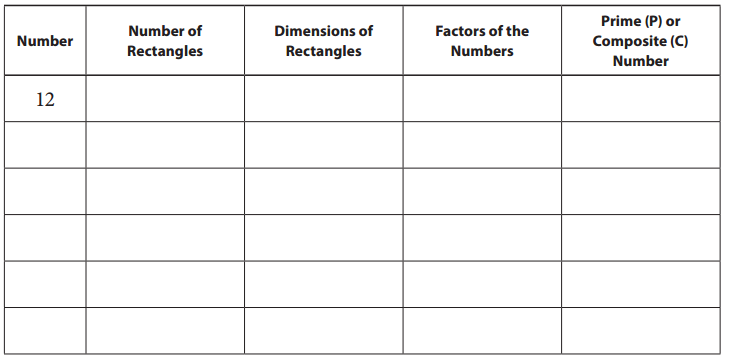
Answer:
We have filled out the given figure. Check the below figure.
Explanation:
Question 2.
Why are some numbers prime and some numbers composite?
Answer:
A prime number has exactly two factors and itself. A composite number is a number that has more than two factors.
Explanation:
Because all natural numbers are either prime or composite but not both. Hence some numbers prime and some numbers composite.
Factors of 36
Use 36 tiles to build each rectangle below. After you build each rectangle, lay red linear pieces along the left side and the top. Then write in the missing dimensions on the sketches below.
Question 1.

Answer:
The missing dimensions are 18.
Explanation:

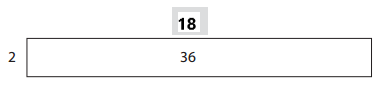
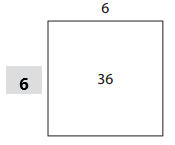
Question 2.
Answer:
The missing dimensions are 18.
Explanation:
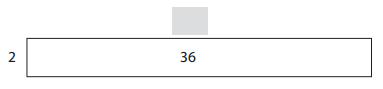
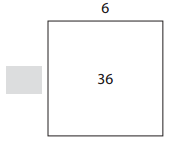
Question 3.
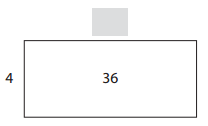
Answer:
The missing dimensions are 9.
Explanation:
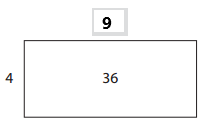
Question 4.
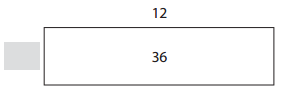
Answer:
The missing dimensions are 3.
Explanation:
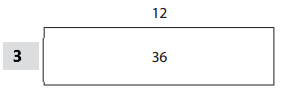
Question 5.
Answer:
The missing dimensions are 6.
Explanation:
Question 6.
The factors of 36 are:
1 and _____, 2 and ____, 4 and ___, ___, and 12, ____ and 6
Answer:
36, 18, 9, 3, and 6.
Explanation:
The factors of 36 are
1 and 36,
2 and 18,
4 and 4,
3 and 12,
6 and 6
Question 7.
Is 36 a prime or a composite number?
a. How do you know?
Answer:
The number 36 is a composite number.
Explanation:
A prime number can only be divided by 1 and itself.
A composite number can be divided by more than 1 and itself.
The factors of 36 are
1, 2, 3, 4, 6, 9, 12, 18, and 36.
Question 8.
Study the list of factors of 36. What patterns do you observe?
Answer:
The list of factors of 36 is 1, 2, 3, 4, 6, 9, 12, 18, and 36.
Explanation:
The patterns we observe here are 2^2 × 3^2
Bridges in Mathematics Grade 4 Student Book Unit 1 Module 2 Session 3 Answer Key
Multiplication Table
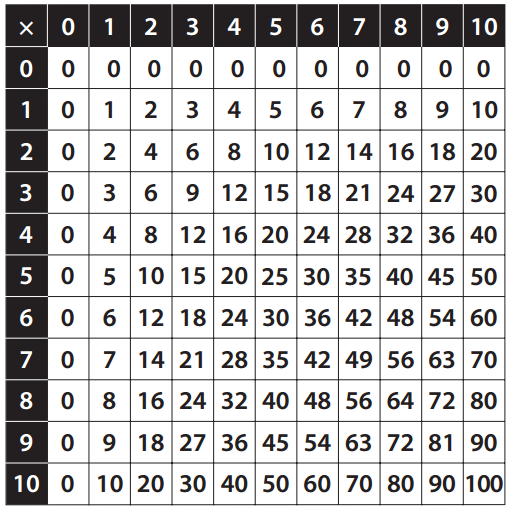
Work Place Instructions 1A Cover Up
Each pair of players needs:
- a 1A Cover Up Record Sheet to share
- 2 spinner overlays
- 4 crayons or colored pencils in different colors
- 1 black crayon or colored pencil
1. Players record their names in the spaces provided on a record sheet.
2. Players take turns spinning the spinners and coloring in arrays with those dimensions. On each turn, players use a black crayon or colored pencil to label the area of the array.
Players talk to their partner about how they found the area.
3. Players will each get 4 turns. Players should use a different color for each array.
4. If a player spins dimensions for an array that will not fit, the player loses that turn unless he can find room to draw two smaller arrays that add up to the area of the array that was spun. The two smaller arrays must both use one of the dimensions spun on that turn.
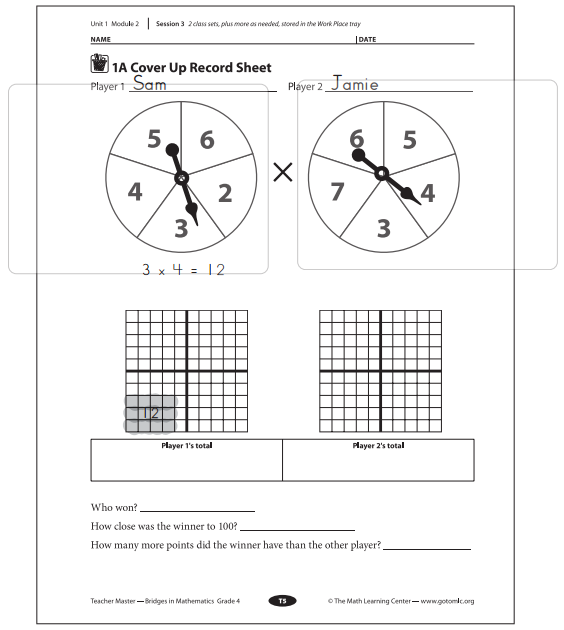
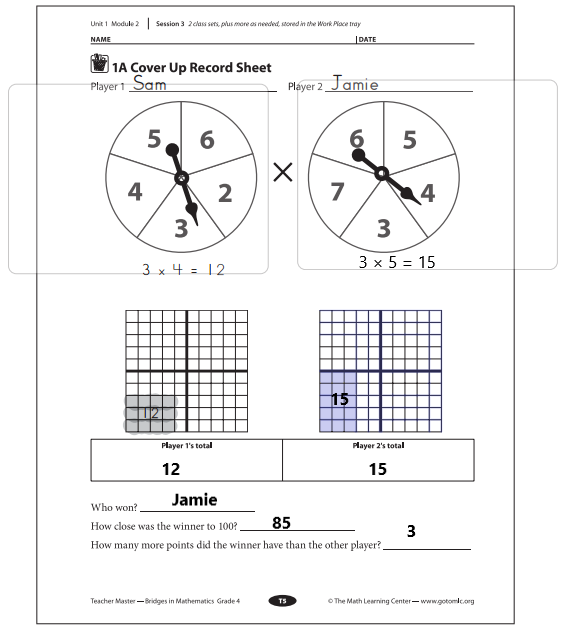
5. After players have both had 4 turns, they determine who got closer to 100 and by how much. They record this information on the record sheet.
6. If players would like to play again, they can get another Cover Up Record Sheet.
Game Variations
A. Players can spin each spinner 5 times and see if they can fit the 5th array in the grid.
B. Players can spin each spinner 5 or more times all at once and then select dimensions for 4 arrays to fit into the grid.
C. If players are having a hard time fitting 4 arrays in the grid, they can play a few games in which they only spin 3 times.
D. Players can play the game with a partner, rather than against a partner, to see how close they can get to 100 working together.
Class Quilt
Mr. Carpenter’s 28 students are making a paper quilt. Each student decorated a square piece of paper. Now, Mr. Carpenter has to decide how to arrange the 28 squares. Help him find the best way to arrange the quilt squares.
Question 1.
How many different ways can Mr. Carpenter arrange the 28 squares? (How many arrays can he make using 28 squares?) Draw the arrangements and label them with their factors.
Answer:
He can make 3 different arrays with 28 squares.
Explanation:
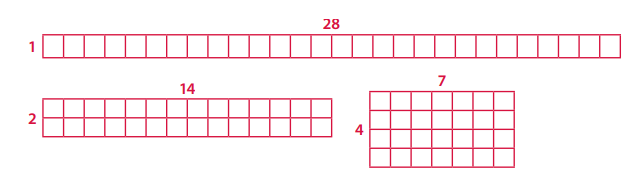
Question 2.
Which arrangement do you think Mr. Carpenter should choose? Why?
Answer:
Mr. Carpenter should choose the third arrangement with factor 4 × 7.
Explanation:
Mr. Carpenter chose the third arrangement with factor 4 × 7 because it is a square shape.
Question 3.
A new student joins Mr. Carpenter’s class. Now he has 29 quilt squares to arrange. How many arrays can he make with 29 quilt squares? Draw the arrays and label them with their factors.
Answer:
He can make 1 arrangement with 29 squares.
Explanation:

Question 4.
CHALLENGE Do you think Mr. Carpenter should use a rectangle to arrange the 29 quilt squares? If not, what shape should he use? Explain your thinking.
Answer:
Bridges in Mathematics Grade 4 Student Book Unit 1 Module 2 Session 4 Answer Key
Work Place Instructions 1B Arrays to One Hundred
Each pair of players needs:
- 2 1B Arrays to One Hundred Record Sheets for each player
- 2 dice numbered 1-6
- 1 die numbered 4-9
- crayons or felt-tip pens and 2 pencils
1. The object of the game is to fill in as much of the grid as possible without going over 100. Students will fill in their own record sheets.
2. The first player rolls any two dice and uses a crayon or colored pen to quickly sketch in an array with those dimensions. If a 1 is rolled, the player can roll again to try to get a bigger number.
3. In the box below the grid, the player writes an equation that describes the array.
4. The player’s partner must agree that the correct product has been shaded in. If it is incorrect, the player must fix it. Partners fill in the grids for each other on their own record sheets.
5. Players take turns rolling any two dice and use a different color pen or crayon to sketch each array.
6. As players’ grids fill up, they might roll an array that won’t fit in one place. Arrays can be broken into smaller arrays. The written equation must show how the player combined smaller arrays to get the product of the numbers rolled.
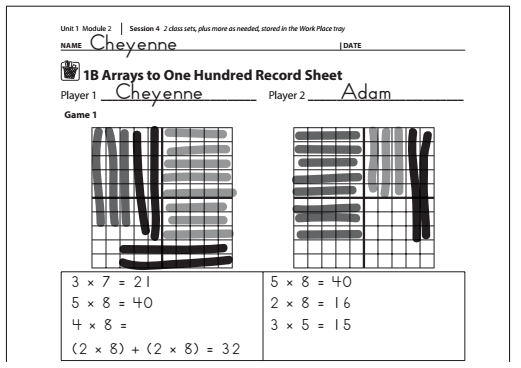
Cheyenne rolled 4 × 8. It would not fit in her grid, so she broke the array into two smaller arrays: (2 × 8) + (2 × 8).
7. If a player rolls an array that can’t fit in his grid, even if it is broken into smaller arrays, that turn is lost.
8. When one player gets close to filling in the entire grid, she can choose to stop rolling the dice. The other player can continue rolling until he wants to stop.
9. The game is over when both players have decided to stop rolling.
10. The player who gets closest to filling in all 100 squares wins the game. Circle the winner on each record sheet.
Game Variation
Partners choose the dice for each other.
Claudia loves to collect shells at the beach. She has a large collection of shells. Today, Claudia is organizing her shells. Write and solve an equation for each problem below.
Question 1.
Claudia made 4 groups with 6 small shells in each group. How many small shells did she use?
Answer:
24 small shells.
Explanation:
Given,
No of groups = 4
No of 6 small shells = 6
To find: How many small shells did she use?
4 × 6 = 24 or 6 × 4 = 24
Question 2.
Claudia made 8 groups with 6 medium-size shells in each group. How many medium sized shells did she use?
Answer:
They have 48 medium size shells.
Explanation:
Given,
No of groups = 8
No of medium size shells = 6
To find: How many medium-sized shells did she use?
8 × 6 = 48
6 × 8 = 48
Question 3.
Claudia made 9 groups with 6 large shells in each group. How many large shells did she use?
Answer:
She used 54 large shells.
Explanation:
Given,
No of groups = 9
No of large shells = 6
9 × 6 = 54 or 6 × 9 = 54
Question 4.
CHALLENGE Claudia had lots of tiny shells. She made three times as many groups of tiny shells as groups of large shells.
a. How many groups of tiny shells did she make?
Answer:
She made 27 groups of tiny shells.
Explanation:
Given,
Claudia made 3 times as many groups of tiny shells
Hence, she made 27 groups of tiny shells.
b. If she put 6 tiny shells in each group, how many tiny shells did she use?
Answer:
She used 162 tiny shells.
Explanation:
Given,
There are 6 tiny shells in each group.
27 × 6 = 162 tiny shells.
Number Line Puzzle
Question 5.
Solve the number line puzzle below:

Answer:

Explanation:
We have solved the number line puzzle.
Bridges in Mathematics Grade 4 Student Book Unit 1 Module 2 Session 5 Answer Key
Multiplying by 4 & 6
Question 1.
Circle all the Double-Doubles facts (×4) in blue. Then solve them and use a regular pencil to write each product.
Answer:
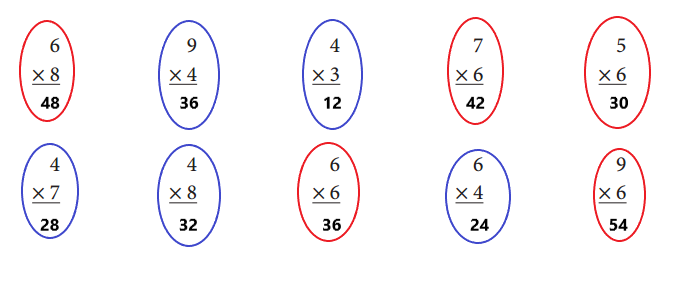
Explanation:
We circled all the Double-Doubles facts (×4) in blue and then solved them. Also used a regular pencil to write each product.
Question 2.
Circle all the Half-Tens Plus One Set facts (×6) in red. Then solve them and use a regular pencil to write each product.
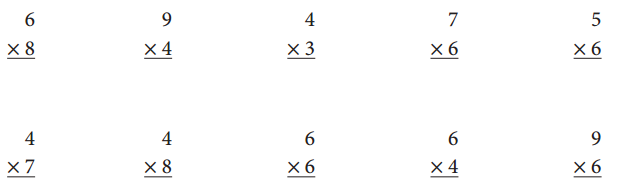
Answer:

Explanation:
I circled all the Half-Tens Plus One Set facts (×6) in red and then solved them. Also used a regular pencil to write each product.
Question 3.
Choose one fact from problem 2 and complete the following steps.
a. Write the fact you chose here: _______
Answer:
The fact we chose here is 6 × 4
Explanation:
From problem 2 we can choose one fact that is 6 × 4.
b. Color in the array for that fact on the grid below.
Answer:
We have colored the array for that fact on the grid below.
Explanation:
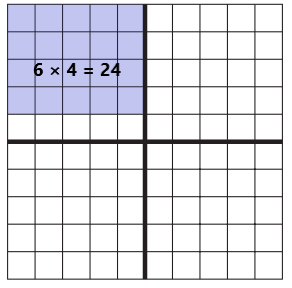
c. Label the array to show how you found the product, and use equations or words to explain your work.
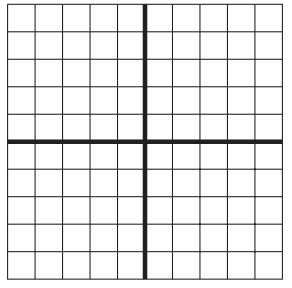
Answer:
We have labeled the array and shown you how to find the product of the array.
Explanation:
Let the length = 6
Width be = 4
Area of the given array is 6 × 4 = 24

Each pair of players needs:
- a 1C Multiple Wheel Record Sheet to share
- 2 dice numbered 1-6
- 2 pencils
1. One player rolls the dice, adds the two numbers, and writes the sum of the numbers in the center of the wheel.
2. Players work together to multiply the number in the center of the wheel times each of the numbers in the middle ring and then write the products in the outside ring.
3. Players take turns recording an equation for each fact in the record sheet chart.
4. Players talk about strategies as they multiply each pair of factors. For example, when multiplying by 9, you can use the Ten Minus One Set strategy.
Student 1 Nines are really hard.
Student 2 I know, but look, we did 10 times 8 already. If we just take away an 8, then we’ll find 9 times 8.
5. When the multiple wheel and chart have been completed, partners discuss and answer the reflection question at the bottom of the record sheet.
Game Variation
Make the game competitive by playing against each other. Roll for the center number and put that number in the middle of the wheel on two separate record sheets. Then see who can complete the wheel faster.
The Multiple Wheel
Question 1.
Fill in the spaces in the multiple wheel.
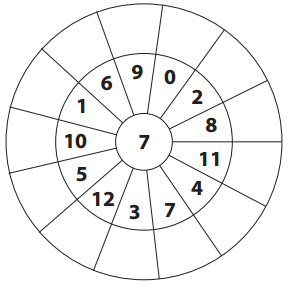
Answer:
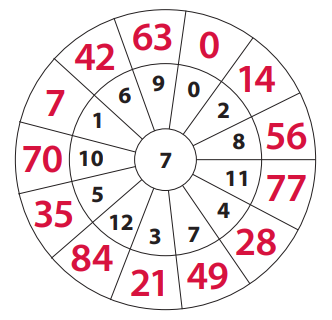
Explanation:
We solved the given equations and filled in the spaces in the multiple wheels.
Question 2.
How did you decide which problems to solve first? Did you use any particular order to solve the problems on the wheel? Explain your thinking.
Answer:
We have decided to solve the problems from a clockwise direction. We can solve the given problems from a clockwise or anti-wise direction.
Question 3.
Solve the equations below:
2 × ____ = 18 ____ × 9 = 36 ____ = 6 × 9 ____ × 8 = 16
4 × ____ = 32 8 × 8 = _____ 3 × 7 = ______ 5 × ____ = 35
Answer:
9, 4, 54, 2, 8, 64, 21, and 7.
Explanation:
2 × 9 = 18 4 × 9 = 36 54 = 6 × 9 2 × 8 = 16
4 × 8 = 32 8 × 8 = 64 3 × 7 = 21 5 × 7 = 35
Question 4.
Is the number 39 prime or composite? Explain your thinking.
Answer:
The number 39 is a composite number.
Explanation:
Yes, the number is composite because 39 has more than two factors i.e. 1, 3, 13, 39. In other words, 39 has more than 2 factors.
Bridges in Mathematics Grade 4 Student Book Unit 1 Module 2 Session 6 Answer Key
Each pair of players needs:
- 2 1D Spinning Around Multiplication Record Sheets
- 1 spinner overlay
- 2 pencils
1. Players take turns spinning over each number circle. On each turn, the player decides what kind of fact was spun. If a fact fits in two categories, only one category is chosen.
2. Each player writes an equation with the factors and their product in the chosen category.
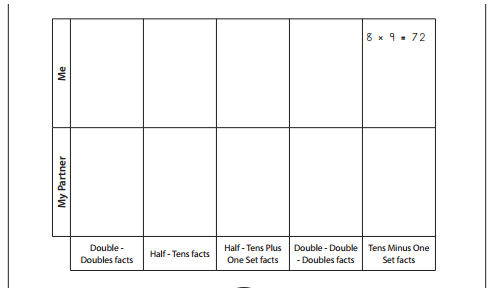
I spun 8 and then 9. It could be Double-Double-Doubles or Tens Minus One Set.
Tens Minus One Set is easier for me, though, so I wrote the equation in the last column.
3. Players record both their own and their partner’s equations on their record sheet.
4. The game ends when one player has at least one equation in each column. Players may have more than one fact in some columns before recording a fact in every column. If the player who took the first turn is the first to get an equation in each column, the other player may take one more turn.
Game Variations
A. Play continues until one player gets at least two facts in every box.
B. Players multiply by each number in one of the number circles by 10, then play as described above. They notice which columns fill and consider whether there are any columns that never get filled.
C. During the game, players consider the probability of being able to fill in each column—which are most likely to be filled in?
Games Problems
Question 1.
Rosa and Jami are playing Spinning Around Multiplication. Rosa spun a 7 and an 8.
a. What is 7 × 8?
Answer:
56.
Explanation:
The answer to the given multiplication is 56.
b. What type of fact did Rosa spin?
Answer:
8 × 7
Explanation:
The fact Rosa used to spun is 8 × 7.
Question 2.
Jami spun a 6 and a 9.
a. What is 6 × 9?
Answer:
54
Explanation:
The answer for 6 × 9 is 54.
b. What type of fact did Jami spin?
Answer:
6 × 9
Explanation:
The type of fact Jami spun is 6 × 9
Question 3.
Carlos and Eli are doing the Multiple Wheel activity. Eli says he can use the fact 3 × 6 to solve 6 × 6. Do you agree or disagree? Explain your thinking.
Answer:
Yes, we can use the fact to solve 6 × 6.
Explanation:
Eli says he can use the fact 3 × 6 to solve 6 × 6.
6 × 3 × 2
So we can solve the multiplication of 3 × 6.
Question 4.
Carlos says he can use the fact 6 × 8 to help him solve 6 × 7 and 6 × 9. Do you agree or disagree? Explain your thinking.
Answer:
No, We don’t agree.
Explanation:
Given,
The given fact is 6 × 8.
6 × 7 and 6 × 9.
There are no factors for 8. Hence we cannot use the fact to solve.
Question 5.
Fill in the ratio table below. Then, circle any numbers in the table that are prime.
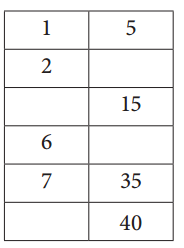
Answer:
We have filled the ratio table below. Also circled numbers in the table that are prime.
Explanation: