Practicing the Bridges in Mathematics Grade 4 Student Book Answer Key Unit 1 Module 3 will help students analyze their level of preparation.
Bridges in Mathematics Grade 4 Student Book Answer Key Unit 1 Module 3
Bridges in Mathematics Grade 4 Student Book Unit 1 Module 3 Session 1 Answer Key
Each pair of players needs:
- a 1E Products Four in a Row Record Sheet to share
- 2 game markers of the same color to share
- 2 pencils
1. Players decide who is going first and who will be X or O.
2 The circled numbers along the left; side of the record sheet are factors. Player 1 places a game marker on one of the factors.
3. Player 2 chooses a second factor by placing the other game marker on a factor. Player 2 draws an X on the product of that factor pair and writes the matching equation in her column of the record sheet.
Player 1 I choose 5 and O’s.
Player 2 I choose 7 and X’s. So I will draw an 18 on 35 because 5 × 7 is 35.
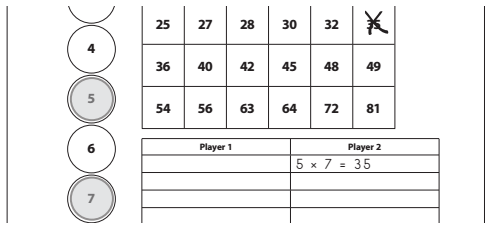
4. Player 1 moves one factor marker to get a new product.
Player 1 I’m moving the factor marker from the 7 to the 4. Since 4 × 5 is 20, I put an O on 20.
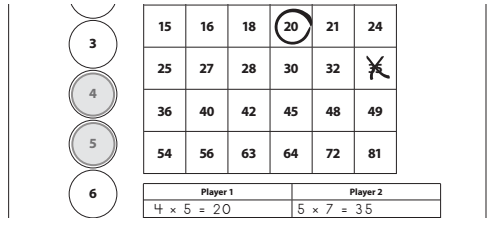
5. Play continues until a player gets four products in a row, across, up and down, or diagonally.
6. Only one of the game markers can be moved during a turn. After choosing a new factor, if the product of the two factors is already marked by an O or an X, the player loses that turn.
7. A marker can be moved so that both markers are on the same factor. For example, if both markers are on 3, the player would mark the product 9 because 3 × 3 = 9.
Game Variations
A. If the player makes a product that is already covered, she can try again.
B. Players use the 1E Products Four in a Row Record Sheet, Variation to play with a game board with fewer factors and fewer products.
Answer:
Product Wheels
Question 1.
Fill in the outer rings for each product wheel.
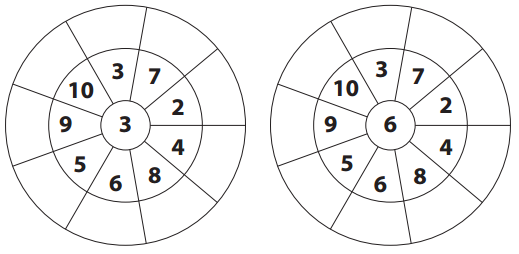
Answer:
Explanation:
We have solved the given equations and filled in the outer rings for each product wheel.
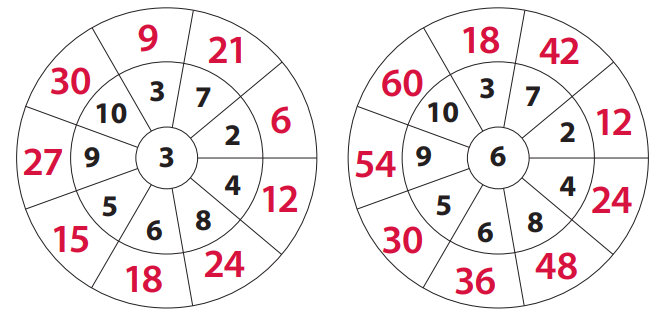
Question 2.
Compare the two product wheels for 3 and 6 above. What pattern do you notice?
Answer:
Even numbers and odd numbers pattern.
Explanation:
By comparing the two product wheels for 3 and 6 above there are even numbers and odd numbers.
For product wheel 3 there are both even and odd numbers.
But in product wheel 6 there are only odd numbers.
Question 3.
Fill in the empty sections of the product wheel below.
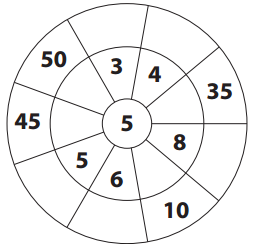
Answer:
Explanation:
We have solved the given equations and filled in the empty sections of the product wheel below.
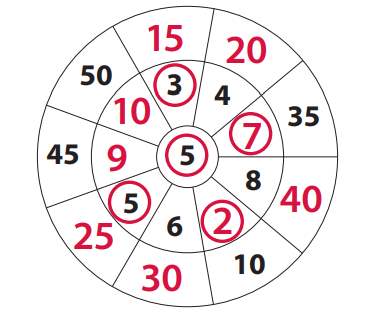
Question 4.
Circle the prime numbers in the product wheel for problem 3.
Answer:
2, 3, 5, 5, and 7.
Explanation:
I have circled the prime numbers in the product wheel for problem 3.

Bridges in Mathematics Grade 4 Student Book Unit 1 Module 3 Session 2 Answer Key
Multiplication & Division Facts
Question 1.
Solve the problems below.
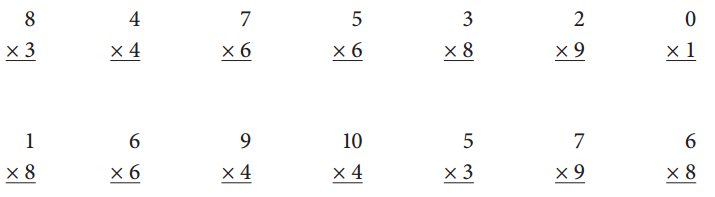
63 ÷ 7 = ____ 42 ÷ 7 = _____ 36 ÷ 4 = ____ 20 ÷ 5 = _____
16 ÷ 8 = ____ 18 ÷ 3 = _____ 6 ÷ 3 = ____ 14 ÷ 2 = _____
Answer:
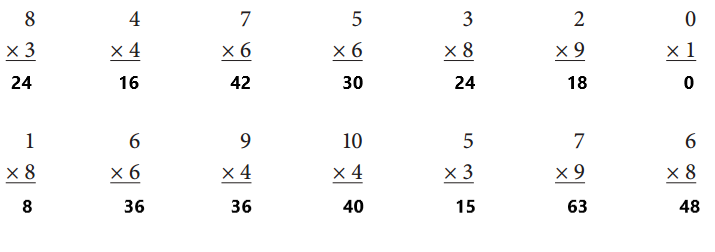
Explanation:
Let us solve the problems given.
63 ÷ 7 = 9
42 ÷ 7 = 6
36 ÷ 4 = 9
20 ÷ 5 = 4
16 ÷ 8 = 2
18 ÷ 3 = 6
6 ÷ 3 = 2
14 ÷ 2 = 7
Question 2.
Circle all the prime numbers in problem 1 (including your answers).
Answer:

Explanation:
I have circled all the prime numbers in problem 1.
Question 3.
Complete the equations.
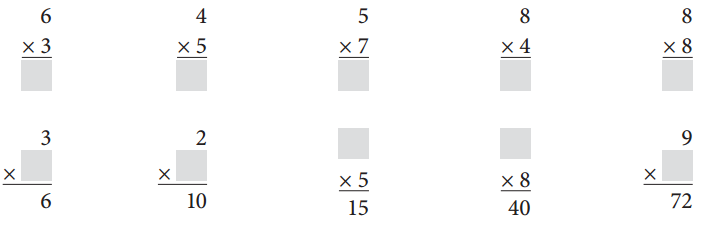
Answer:
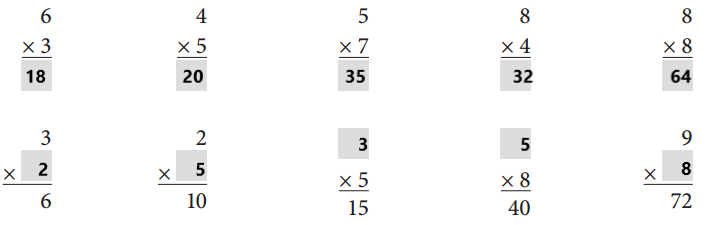
Explanation:
We have completed the equations. Check the above figure.
Question 4.
How can you use the answer to 4 × 8 to solve 4 × 16? Draw an array and then use numbers or words to explain your answer.
Answer:
The answer is 32 and 64.
Explanation:
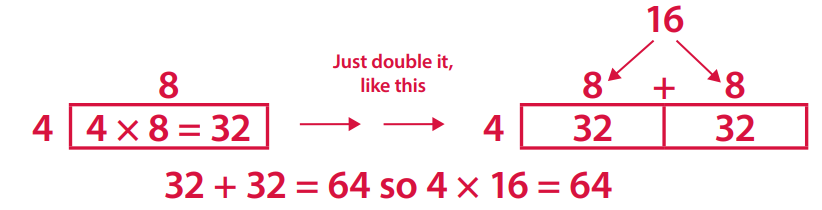
Bridges in Mathematics Grade 4 Student Book Unit 1 Module 3 Session 3 Answer Key
More Multiplicative Comparisons at the Giant’s Door
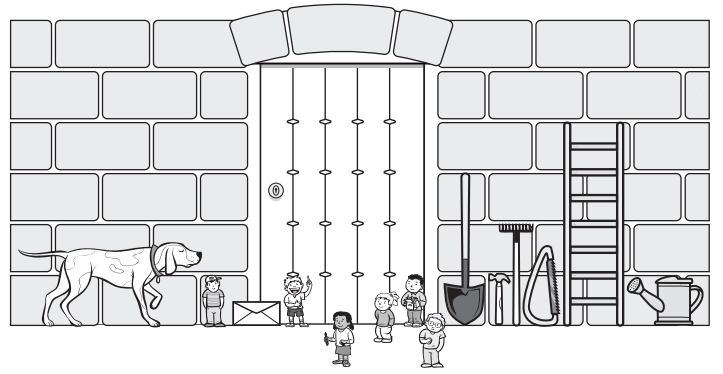
The giant’s hammer is 48” tall. Use this information to solve the problems below. Show your work and write an equation to represent each situation.
Question 1.
The shovel is ______ times as tall as the hammer. The shovel is ______ inches tall.

Answer:
The shovel is 3 times as tall as the hammer. Hence the shovel is 144 inches tall.
Explanation:
Given,
The giant’s hammer is 48” tall.
The shovel is 3 times as tall as the hammer.
48 × 3 = 144
Hence the shovel is 144 inches tall.
Question 2.
The ladder is times as tall as the hammer. The ladder is inches tall.

Answer:
The ladder is 4 times as tall as the hammer. The ladder is 192 inches tall.
Explanation:

Question 3.
The wooden door is times as tall as the hammer. The door is inches tall.

Answer:
The wooden door is 5 times as tall as the hammer. The door is 240 inches tall.
Explanation:

Question 4.
The envelope is ____ as tall as the hammer. The envelope is ____ inches tall.

Answer:
The envelope is half as tall as the hammer. The envelope is 24 inches tall.
Explanation:

Question 5.
CHALLENGE The dog is ____ times as tall the hammer. The dog is ____ inches tall.

Answer:
The dog is 2 times as tall as the hammer. The dog is 96 inches tall.
Explanation:

Question 6.
Fill in the bubble beside the equation that best represents each situation below. (Note: The letter i stands for inches.)
a The hammer is 48 inches tall. The rake is 2 times as tall as the hammer. How tall is the rake?
![]() 48 ÷ 2 = i
48 ÷ 2 = i
![]() 48 + 2 = i
48 + 2 = i
![]() 48 × 2 = i
48 × 2 = i
Answer:
The answer is 48 × 2 = i.
Explanation:
Given,
The hammer is 48 inches tall.
The rake is 2 times as tall as the hammer.
48 × 2 = 96
b. The ladder is 192 inches tall. That is 4 times as tall as the watering can. How tall is the watering can?
![]() 192 ÷ 4 = i
192 ÷ 4 = i
![]() 192 × 4 = i
192 × 4 = i
![]() 192 + 4 = i
192 + 4 = i
Answer:
The answer is 192 ÷ 4 = i.
Explanation:
Given,
The ladder is 192 inches tall.
That is 4 times as tall as the watering can
192 ÷ 4 = i.
Question 7.
The saw is 72 inches tall. The envelope is 24 inches tall. How many times taller is the saw than the envelope? Show your work and write the answer on the line below.
The saw is ____ times as tall as the envelope.
Answer:
The saw is 3 times as tall as the envelope.
Explanation:
Given,
The saw is 72 inches tall.
The envelope is 24 inches tall.
72 ÷ 24 = 3
Hence, The saw is 3 times as tall as the envelope.
Drawing Comparisons & Writing Equations
You will need a ruler marked in centimeters to do some of these problems.
Question 1.
In the space below, draw a horizontal line that is exactly 5 centimeters long. Below that line, draw another horizontal line that is exactly 3 times as long as the first. Write a multiplication equation that gives the length of each line and tells how many times longer the second line is than the first.
![]()
Answer:
The length of each line is 5 cm times longer than the second line is than the first.
Explanation:
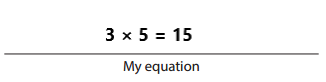
My equation is 3 × 5 = 15 cm.
Question 2.
Here are two lines. Use them to answer the questions below.
A _______
B __________
a. If you just look at both lines, how many times as long is line B than line A? Make an estimate without measuring the lines.
It looks like line B is _____ times as long as line A.
Answer:
It looks like line B is 3 cm times as long as line A.
Explanation:
If we just look at both lines, It looks like line B is 3 cm times as long as line A.
b. Now measure and label both lines in centimeters. How many times as long is line B than line A? Write an equation to show.
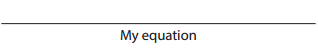
Answer:
4 times as long is line B than line A.
Explanation:
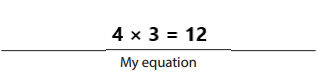
Question 3.
Adam Ant crawled 7 centimeters. Angela Ant crawled twice as far as Adam. Measure, draw, and label a line to show how far Angela Ant crawled.
Answer:
14 cm.
Explanation:
Given,
Adam Ant crawled 7 centimeters.
Angela Ant crawled twice as far as Adam.
7 × 2 = 14 cm
Bridges in Mathematics Grade 4 Student Book Unit 1 Module 3 Session 4 Answer Key
Work Place Instructions 1F Dragon’s Gold
Each pair of players needs:
- 1 1F Dragon’s Gold Record Sheets (players need to agree on which version of the sheet they’re going to use)
- 1 die to share, numbered 1-6 for use with Record Sheet A or numbered 4-9 for use with Record Sheet B
- 1 clear spinner overlay to share
- a regular pencil for each player
1. The object of the game is to mark 5 boxes in a row, going horizontally, vertically, or diagonally. Players each fill in their own record sheet.
2. The first player rolls the die and spins the spinner at the top of his record sheet, and then multiplies the number rolled by the number of times indicated on the spinner.
3. The player then finds the product on his record sheet and records a statement of multiplicative comparison below the number, using an equation that starts with the product.
For example, if the player rolls a 4 and lands on 6 times as many when he spins, he multiplies 6 × 4 to get 24. Then he finds 24 on his record sheet and writes 24 = 6 × 4 below the number to represent the fact that 24 is 6 times as many as 4.

4. The second player takes her turn. Play continues until one of the players has written equations in 5
boxes in a row, horizontally, vertically, or diagonally.
- If a player rolls and spins a product that shows up more than once on the record sheet, he writes an equation in only one of the boxes, not both.
- Players should look for duplicate products on their record sheets, and choose carefully to increase their chances of marking 5 boxes in a row.
• If a player spins and rolls a product she has already marked on her sheet, and there is no duplicate, she can write the equation in the dragon’s box at the center of the sheet. This is allowed once. After that, the player loses her turn and play goes to her partner.
5. The game is over when one of the partners has written an equation in 5 boxes in a row, horizontally, vertically, or diagonally.
Game Variation
A. Partners use a die numbered 4-9 and 2 copies of the 1F Dragon’s Gold Record Sheet B. The game is played the same way, but now students are working with multiplicative comparisons up to 90 = 10 × 9.
More Multiplicative Comparisons
Question 1.
The equation 45 = 5 × 9 can mean (fill in the bubble beside every true sentence):
![]() 45 is the same as 5 groups of 9
45 is the same as 5 groups of 9
![]() 45 is 5 times as many as 9
45 is 5 times as many as 9
![]() 45 is 5 less than 9
45 is 5 less than 9
![]() 45 is the same as 9 groups of 5
45 is the same as 9 groups of 5
Answer:
The answers are 45 is the same as 5 groups of 9, 45 is 5 times as many as 9 and 45 is the same as 9 groups of 5.
Explanation:
Given,
The equation 45 = 5 × 9
45 is the same as 5 groups of 9
45 = 5 × 9
45 is 5 times as many as 9
45 = 5 × 9
45 is the same as 9 groups of 5
45 = 9 × 5
Question 2.
Fill in the bubbles beside the two equations that best represent this situation:
Dante has 36 baseball cards. That is 4 times as many as his friend, Andrew, has. How many baseball cards does Andrew have? (In the equations below, b stands for Andrew’s baseball cards.)
![]() 4 × b = 36
4 × b = 36
![]() 36 × 4 = b
36 × 4 = b
![]() 36 + 4 = b
36 + 4 = b
![]() 36 ÷ b = 4
36 ÷ b = 4
Answer:
The answers are 4 × b = 36 and 36 ÷ b = 4.
Explanation:
Given,
Dante has 36 baseball cards.
That is 4 times as many as his friend.
36 ÷ 4 = 9
Question 3.
Write and solve an equation for each of these problems.
a. Sara is 12 years old. Sara’s mom is 3 times older than Sara. How old is Sara’s mom?
Answer:
Sara’s mom is 36 years old.
Explanation:
Given,
Sara is 12 years old.
Sara’s mom is 3 times older than Sara
12 × 3 = 36 years old.
b. David bought a jacket and a T-shirt. The jacket cost 4 times as much as the T-shirt. The T-shirt cost $20. How much did the jacket cost?
Answer:
$80
Explanation:
Given,
The cost of the T-shirt is $20
The jacket cost 4 times as much as the T-shirt
$20 × 4 = $80
c. Jenny bought a book and a DVD. The book cost $21. That was 3 times more than the DVD. How much did the DVD cost?
Answer:
$7
Explanation:
Cost of book = $21
That was 3 times more than the DVD.
$21 ÷ 3 = $7
Question 4.
CHALLENGE Daniel rode his bike 5 kilometers. His friend, Briana, rode 8 times as far. Her friend, Ted, rode half as far as Briana. How far did Ted ride? Show all your work.
Answer:
20 km.
Explanation:
Daniel rode his bike for 5 kilometers.
His friend, Briana, rode 8 times as far
5 × 8 = 40
Her friend, Ted, rode half as far as Briana
40 ÷ 2 = 20 km.
Bridges in Mathematics Grade 4 Student Book Unit 1 Module 3 Session 5 Answer Key
All in the Family
Question 1.
Fill in the missing number in each triangle. Then write the facts in the fact family.
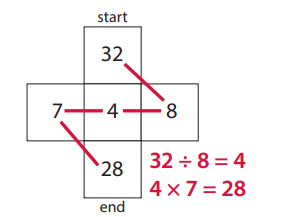
ex
2 × 8 = 16
8 × 2 = 16
2 × 8 = 16
16 ÷ 8 = 2
16 ÷ 2 = 8
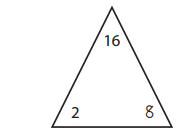
a.
______ × _____ = ______
______ × _____ = ______
______ ÷ _____ = ______
______ ÷ _____ = ______
Answer:
The missing number for the given triangle is = 3
Explanation:
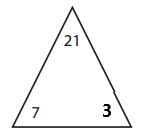
7 × 3 = 21
3 × 7 = 21
21 ÷ 3 = 7
21 ÷ 7 = 3
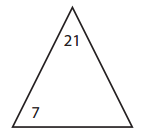
b.
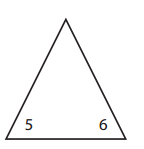
______ × _____ = ______
______ × _____ = ______
______ ÷ _____ = ______
______ ÷ _____ = ______
Answer:
The missing number for the given triangle is 30.
Explanation:
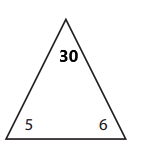
3 × 6 = 18
6 × 3 = 18
30 ÷ 5 = 6
30 ÷ 6 = 5
c.

______ × _____ = ______
______ × _____ = ______
______ ÷ _____ = ______
______ ÷ _____ = ______
Answer:
The missing number for the given triangle is 8.
Explanation:
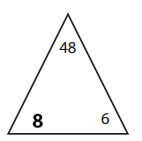
8 × 6 = 48
6 × 8 = 48
48 ÷ 8 = 6
48 ÷ 6 = 8
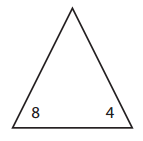
d.
______ × _____ = ______
______ × _____ = ______
______ ÷ _____ = ______
______ ÷ _____ = ______
Answer:
The missing number for the given triangle is 8.
Explanation:
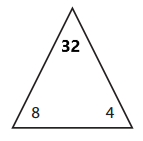
8 × 4 = 32
4 × 8 = 32
32 ÷ 4 = 8
32 ÷ 8 = 4
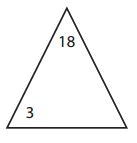
e.
______ × _____ = ______
______ × _____ = ______
______ ÷ _____ = ______
______ ÷ _____ = ______
Answer:
The missing number for the given triangle is 6.
Explanation:
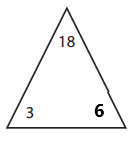
3 × 6 = 18
6 × 3 = 18
18 ÷ 3 = 6
18 ÷ 6 = 3
Question 2.
CHALLENGE Use multiplication and division to find the secret path through each maze. You can only move one space up, down, over, or diagonally each time. Write two equations to explain the path through the maze.
ex
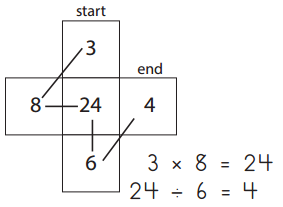
a.
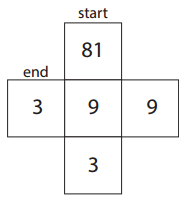
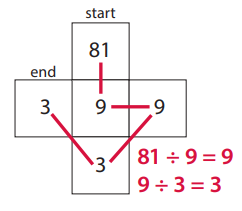
Answer:
9, 3
Explanation:
b.
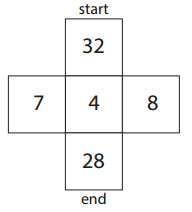
Answer:
The answer is 4 and 28.
Explanation: