Printable Worksheets on Volume available here will assist students in learning about the concept volume. In this Worksheet on Volume, you will find Volume Questions for different shapes, such as a rectangular prism, sphere, cone, cylinders, triangular prisms, etc. You can get an idea of volume in terms of square units such as counting or estimating the number of blocks(square units) shown.
Furthermore, our Volume Worksheets with Solutions will assist you in how to solve the different models of problems with detailed explanations. In fact, it has Volume Questions ranging from easy ones to the most difficult ones keeping in mind all kinds of students. Both Teachers and Students of 5th Grade Math can use this Math Worksheet on Volume to know the formulas for the volume, how to find the volume of simple shapes.
Do Refer Articles on Volume of Simple Shapes:
- Worksheet on Volume of a Cube and Cuboid
- Worked out Problems on Volume of a Cuboid
- Volume of Cubes and Cuboids
Volume Worksheets with Answers
Example 1.
Find the volume of a cube of side 23 cm?
Solution:
Given,
side of the cube s=23 cm
The volume of the cube=s3
v=233
=12,167 cm3
Hence, the volume of the cube is 12,167 cm3.
Example 2.
Find the volume of a cube of side 12cm?
Solution:
Given,
side of the cube s=12 cm
The volume of the cube=s3
v=123
=1728
Hence, the volume of the cube is 1728 cm3.
Example 3.
Find the volume of a cube of side 19cm?
Solution:
Given,
side of the cube s=19 cm
The volume of the cube=s3
v=193
=6859
Hence, the volume of the cube is 6859 cm3.
Example 4.
Find the volume of a cuboid of dimension 12 cm × 110 mm × 140 mm in cubic cm?
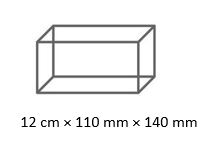
Solution:
Given,
The dimension of the cuboid is 12 cm × 110 mm × 140 mm
i.e. length of the cuboid is=12 cm
The breadth of the cuboid=110 mm=11 cm
Height of the cuboid=140 mm=14 cm
The volume of the cuboid=12.11.14
=1848 cm3
Hence, the volume of the cuboid is 1848 cm3.
Example 5.
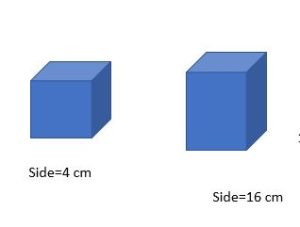
How many cubes of side 4 cm are required to build a cube of side 16 cm?
Solution:
The side of the small cube = 4 cm
The side of the big cube = 16 cm
Let the number of small cubes required = n
The volume of the cube v=s3
n=volume of big cube/volume of small cube
The volume of small cube=43
=64
The volume of big cube=163
=4096
n=4096/64=64
Therefore, 64 cubes of side 4 cm are required to build a cube of 16 cm.
Example 6.
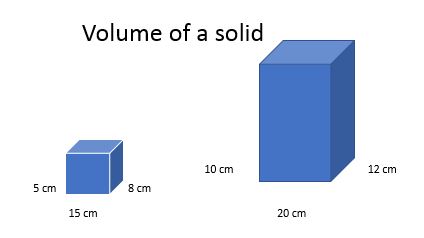
Find the volume of the below solid figure
Solution:
Given
length of the first solid is=15 cm
The breadth of the first solid=8 cm
height of the first solid=5 cm
The volume of the first solid=lbh
=15.8.5
=600 cm3
Hence, the volume of the first solid is 600 cm3
2. Given
length of the first solid is=20 cm
The breadth of the first solid=12 cm
height of the first solid=10 cm
The volume of the first solid=lbh
=20.12.10
=2400 cm3
Hence, the volume of the second solid is 2400 cm3
Example 7.
A cubical of wood was cut into 10 equal cubes of sides 5 cm. What is the volume of the block of wood?
Solution:
Given,
A cubical of wood was cut into 10 equal cubes of sides 5 cm
The volume of 1 cube=5.5.5=125 cm3
The volume of 10 cubes or block of wood=10 × 125=1250 cm3
Hence, the volume of the block of wood is 1250 cm3.
Example 8.
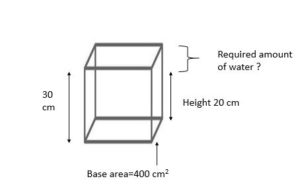
A rectangular container with a base area of 400 cm2 is filled with water to a height of 20 cm. If the container has a height of 30 cm, how much water (in liters) should be added to it to fill it completely?
Solution:
Given,
base area=400 cm2
base area=length × breadth=400 cm2
volume(20 cm)=length ×breadth × height(20 cm)
=400 × 20
=8000 cm3
To convert cm3 into liters, we have to divide it by 1000.
=8000/1000 liters
=8liters
volume(30 cm)=length ×breadth × height(30 cm)
=400 × 30
=12000 cm3
To convert cm3 into liters, we have to divide it by 1000.
=12000/1000 liters
=12 liters
how much water (in liters) should be added to it to fill it completely is 12-8=4 liters
Hence, 4 liters of water is to be added to fill it completely.
Example 9.
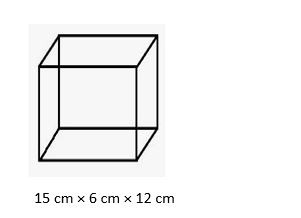
Find the volume of oil that can be poured into a container of dimensions 15 cm × 6 cm × 12 cm?
Solution:
Given,
Length of the container=15 cm
The breadth of the container=6 cm
The height of the container=12 cm
volume=length × breadth × height
=15 cm× 6 cm × 12 cm
=1080 cm3
To convert cm3 into liters, we have to divide it by 1000.
=1080/1000 liters
=1.08 liter
Hence 1.08 liter of oil can be poured into the container.
Example 10.
Find the volume of the water present in the container of dimensions 18 cm × 4 cm × 10 cm?
Solution:
Given,
Length of the container=18 cm
The breadth of the container=14 cm
The height of the container=10 cm
volume=length × breadth × height
=18 cm× 14 cm × 10 cm
=2520 cm3
To convert cm3 into liters, we have to divide it by 1000.
=2520/1000 liters
=2.52 liter
Hence 2.52 liter of water is present in the container.
