To Find the Highest Common Factor of Three numbers by using Division Method | HCF of 3 Numbers by Division Method

On this page, you will learn about Finding the HCF of Three Numbers using the Division Method, Example problems on Finding the Highest Common Factor of given three numbers by using the Division Method. To get the HCF of 3 Numbers we write the given numbers, identify the small number and larger numbers, then divide the numbers by the smallest number.

The Highest Common Factor (HCF) of the two numbers is the highest number among all the common factors of the given numbers. The HCF for two numbers or three numbers is the same. We have covered different questions with a brief explanation on finding HCF, Shortcut to find HCF of Three Numbers, HCF of 3 Numbers Formula, to enhance their math skills as well as provide them with better practice. It will help them to know which number is divisible and which isn’t.

Read More Articles:

• Examples of Highest Common Factor
• Examples to find Highest Common Factor of two numbers by using Division Method
• To find Highest Common Factor by using Prime Factorization Method
• Examples to find Highest Common Factor by using Prime Factorization Method

How to find HCF of 3 Numbers using the Division Method?

The process of finding the Highest factor is easy and requires students to be familiar with its formula. Students need to have proper knowledge of multiplication and division for attempting the questions on HCF of 3 Numbers. They are as follows

Step 1: First, identify the smaller number in the given three numbers.
Step 2: Next, write the first small number as the divisor and the second smaller number as a dividend. Then continue the division process till you get the remainder as 0. The Number that exactly divides is the HCF of the first two numbers.
Step 3: Find the HCF of the third number, using the founded HCF of the first two numbers value as the divisor and the third number as a dividend.
Step 4: The Highest Common Factor you get in step 3 will be the HCF value of the three numbers.

HCF of 3 Numbers Using Division Method

Example 1.
Find the HCF of 30, 45, 75. Using the Division Method?

Solution:
Given the values are 30, 45, and 75.
Now, we need to find out the factors using the division method.
First, in the division, find the HCF value of the first two least numbers that are 30, and 45.

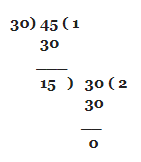
So, 15 is exactly the divided prime factor of 30 and 45.
Now, find the HCF of the third number with the HCF of the first two numbers. The third number is the dividend and the HCF of the first two numbers is a divisor.
The HCF of 15, 75 are,

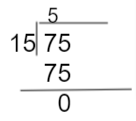
Hence, 15 is the HCF of 15, and 75.
Therefore, the HCF of the given three numbers is 15.

Example 2.
What is the HCF of 5, 7, 9? Using the division method?

Solution:
As given in the question, the values are 5, 7, 9.
Now, we have to find the HCF.
In the division, the smallest number is the divisor and the larger number is the dividend. So, the HCF of 5, and 7 is
`
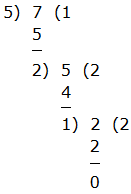
Thus, the HCF of 5, and 7 is 1.
Now, find the HCF of 1, and 9 is

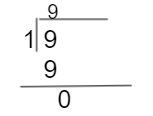
So, the factors of 1, and 9 are 1.
Therefore, the HCF of the given three numbers 5, 7, and 9 is 1.

Example 3.
Find the HCF of 108, 288, 40 using the Division Method.

Solution:
Given the numbers are 108, 288, and 360.
Using the division method, find the Highest Common Factor,
Now, the division operation, in between 108 and 288. Then,

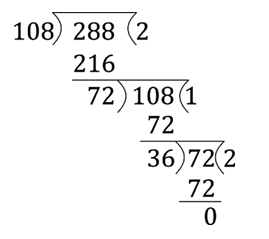
Hence, the HCF of 108, and 288 is 36.
Next, the HCF of the 36, and 360.

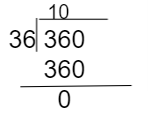
The HCF of 36, 360 is 36.
Hence, the HCF of three given numbers 108, 288, 360 is 36.

Example 4.
What is the HCF of 629, 1517, and 703? Using the Division Method?

Solution:
As given in the question, the values are 629, 1517, and 703.
Now, we are going to find the HCF using the division method.
In this three numbers division method, find the HCF of 629 and 1517, then find the HCF of the first two numbers HCF values, 703.
After performing the division operation, the HCF value of 629, and 1517 is 37.
Next, the HCF of 37 and 703 is 37. The below shows the figure how to perform the division operation of three given numbers,

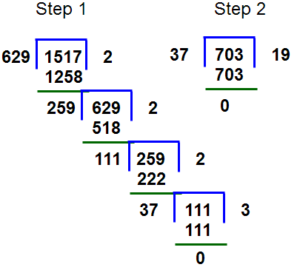
Therefore, the HCF of 629, 1517, 703 is 37.

Example 5.
Find the HCF of 15, 25, and 75 using the division method.

Solution:
Given the HCF finding values are 15, 25, and 75.
Using the division method, we are going to find the HCF.
The HCF of 15, and 25 is

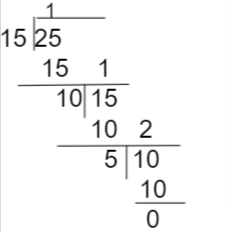
Hence, the Highest Common factor of 15, and 25  is 5.
Now, find the HCF of 5, and 75 is

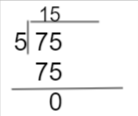
Thus, 5 is exactly the divided prime factor of 5 and 75.
Therefore, the HCF of the given three numbers 15, 25, 75 is 5.

Students who wish to become masters in 5th Grade Math are suggested to refer to our articles on a frequent basis and understand the concepts within.

FAQ’s on HCF of Three Numbers Using the Division Method

1. What are the tricks and formulas to find HCF?

The below are the formulas and tricks to find HCF is,

• If any two numbers are said to be co-prime their HCF is 1.
• Product of any two given numbers = product of HCF and LCM.
• HCF = HCF of Numerators/LCM of denominators.

2. Write the relation between HCF and LCM?

The LCM and HCF are related as by the formula is:
LCM (a, b) = a × b/HCF(a,b)
Where a, and b are the two different given numbers.

3. What’s Highest Common Factor?

HCF is the process of finding the Highest of the common factor of two or more numbers.

4. How to find the HCF of three numbers using the Division Method?

To find out the HCF of three given numbers using the division method,
Step 1: First, Determine the HCF of any two numbers.
Step 2: Next, find out the HCF of the third number and therefore the HCF obtained in step 1.
Step 3: HCF obtained in step 2 is going to be the HCF of the three numbers.