This handy Spectrum Math Grade 7 Answer Key Chapter 7 Lesson 7.3 Calculating Probability provides detailed answers for the workbook questions
Spectrum Math Grade 7 Chapter 7 Lesson 7.3 Calculating Probability Answers Key
The probability of an event is the measure of how likely it is that the event will occur.
Probability (P) =

A bag contains 12 marbles, 7 blue and 5 red. If a marble is chosen at random, the probability that it will be red is:
Probability (P) =
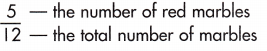
Solve each problem. Write answers as fractions in simplest form.
Question 1.
A bag contains 5 blue marbles, 3 red marbles, and 2 white marbles. What is the probability a selected marble will be red? _____________
What is the probability that a selected marble will not be white? _____________
What is the probability that a selected marble will be either blue or white? _____________
Answer:
The probability of selected marble will be red is probability(p) = \(\frac{3}{10}\),
The probability that a selected marble will not be white is probability(p) = \(\frac{4}{5}\),
The probability that a selected marble will be either blue or white is probability(p) = \(\frac{7}{10}\),
Explanation:
Given no. of blue marbles are 5,no of red marbles are 3 and no. of white marbles are 2, so total no. of outcomes are 5 + 3 + 2 = 10, therefore probability of selected red marble is 3/10; probability that selected marble will not be white is 8/10=4/5; probability that a selected marble will be either blue or white is 5 + 2 = 7 that is 7/10.
Use the spinner to find the following probabilities. Write answers as fractions in simplest form.
Question 2.
P (3) = _______________
Answer:
\(\frac{1}{6}\),
Explanation:
Given from the spinner no. of outcomes are 6 and no. of 3’s are 1 so probability of 3 is p(3) = 1/6
Question 3.
P (odd) = _______________
Answer:
\(\frac{1}{2}\),
Explanation:
Given from the spinner no of odd numbers are 1,3,5 = 3 so, p(odd) = 3/6 = 1/2.
Question 4.
P (1 or 4) = _______________
Answer:
\(\frac{1}{3}\),
Explanation:
Given from the spinner probability of p(1 or 4) is 2/6 = 1/3.
Question 5.
P ( > 4) = _______________
Answer:
\(\frac{1}{3}\),
Explanation:
Given from the spinner probability greater than 4 is 5 and 6 that is 2, so p ( >4) = 2/6 = 1/3
Question 6.
P ( < 6) = _______________
Answer:
\(\frac{5}{6}\),
Explanation:
Given from the spinner p (<6) is 5, no. of outcomes are 6 so p(<6) = 5/6.
Question 7.
P (not 5 or 3) = _______________
Answer:
\(\frac{2}{3}\),
Explanation:
Given from the spinner not 5 or 3 means remaining numbers are 4 so p (not 5 or 3) = 4/6 = 2/3.
Probability can also be thought of as the ratio of desired outcome(s) to the sample space. It can be expressed as a ratio, fraction, decimal, or percent.
When tossing a coin, what is the probability that it will land on heads?
Desired outcome: heads sample space: heads, tails probability: 1:2, \(\frac{1}{2}\), 50%, 0.5.
Find the probability. Write answers as fractions in simplest form.
A box contains 3 red pencils, 4 blue pencils, 2 green pencils, and I regular pencil. If you take I pencil without looking, what is the probability of picking each of the following?
Question 1.
a red pencil ______________
Answer:
\(\frac{3}{10}\),
Explanation:
Given no. of red pencils are 3 and no. of outcomes are 3 + 4 + 2 + 1= 10, so probability(p) of picking a red pencil is 3/10.
Question 2.
a blue pencil ______________
Answer:
\(\frac{2}{5}\),
Explanation:
Given no. of blue pencils are 4, probability (p) of blue pencil is 4/10 = 2/5.
Question 3.
a green pencil ______________
Answer:
\(\frac{1}{5}\),
Explanation:
Given no. of green pencil are 2 so probability(p) of green pencil is 2/10 = 1/5.
Question 4.
a regular pencil ______________
Answer:
\(\frac{1}{10}\),
Explanation:
Given no of regular pencil is 1 so probability (p) of regular pencil is 1/10.
If you spin the spinner shown at the right, what is the probability of the spinner stopping on each of the following?
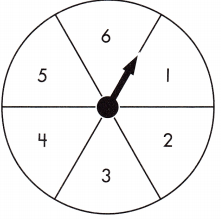
Question 5.
a letter ______________
Answer:
\(\frac{1}{2}\),
Explanation:
Given from the spinner total number of outcomes are 6 and no. of letters are A,B,C is 3 that is 3/6 = 1/2.
Question 6.
an odd number ______________
Answer:
\(\frac{1}{3}\),
Explanation:
Given from the spinner the odd numbers are 1, 3 that is 2 odd numbers and total outcomes are 6, so probability(p) of odd number is 2/6 = 1/3.
Question 7.
an even number ______________
Answer:
\(\frac{1}{6}\),
Explanation:
Given from the spinner even number is 2 that is 1, so probability of even number is (p) is 1/6.
Question 8.
a vowel ______________
Answer:
\(\frac{1}{6}\),
Explanation:
Given from the spinner vowel is A that is 1 vowel so probability(p) of a vowel is 1/6.
Question 9.
the number 3 ______________
Answer:
\(\frac{1}{6}\),
Explanation:
Given from the spinner no. of 3 is 1 so probability(p) of the number 3 is 1/6.
Question 10.
a consonant ______________
Answer:
\(\frac{1}{3}\),
Explanation:
Given from the spinner consonant are B,C that is 2 so probability(p) a consonant is 2/6 = 1/3.
Determine the probability for each of the following events. Write answers as fractions in simplest form.

Question 1.
drawing a gray marble ______________
Answer:
\(\frac{1}{2}\),
Explanation:
Given from the event total number of outcomes are 10 and no. of grey marble are 5, so probability of drawing a grey marble is 5/10 = 1/2.
Question 2.
drawing a white marble ______________
Answer:
\(\frac{3}{10}\),
Explanation:
Given from the event no of white marbles are 3 so probability of drawing a white marble is 3/10.
Question 3.
drawing a black marble ______________
Answer:
\(\frac{1}{5}\),
Explanation:
Given from the event no. of black marble are 2 so probability of black marble is 2/10 = 1/5.
Question 4.
drawing either a gray or a black marble ______________
Answer:
\(\frac{7}{10}\),
Explanation:
Given from the spinner no of drawing either grey or black marble are 5 + 2= 7 so probability is 7/10.
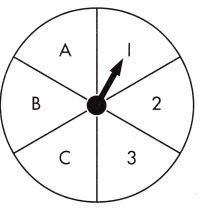
Question 5.
spinning a gray section ______________
Answer:
\(\frac{1}{3}\),
Explanation:
Given from the spinner total no. of outcomes are 12 and no. of spinning a grey section is 4 so probability is 4/12 = 1/3.
Question 6.
spinning a 4 ______________
Answer:
\(\frac{1}{6}\),
Explanation:
Given from the spinner no of 4 is 2 so the probability of spinning a 4 is 2/12 = 1/6.
Question 7.
spinning a 1 ______________
Answer:
\(\frac{1}{6}\),
Explanation:
Given from the spinner no of 1 is 2 so the probability of spinning a 1 is 2/12 = 1/6.
Question 8.
spinning either a 4 or 5 ______________
Answer:
\(\frac{5}{12}\),
Explanation:
Given from the spinner total no. of 4 and 5 is 5 so, the probability of spinning either a 4 or 5 is 5/12.
Question 9.
spinning an even number ______________
Answer:
\(\frac{1}{3}\),
Explanation:
Given from the spinner even numbers are 4,6,4,2 that is 4 so probability of spinning an even number is 4/12 = 1/3.
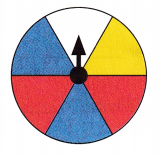
Question 10.
spinning a red section ______________
Answer:
\(\frac{1}{3}\),
Explanation:
Given from the spinner no. of red section are 2 and total no. of outcomes are 6, so probability of spinning a red section is 2/6 = 1/3.
Question 11.
spinning a blue section ______________
Answer:
\(\frac{1}{3}\),
Explanation:
Given from the spinner no. of blue sections are 2 so probability of spinning a a blue section is 2/6 = 1/3.
Question 12.
spinning a yellow section ______________
Answer:
\(\frac{1}{6}\),
Explanation:
Given from the spinner no. of yellow sections are 1 so probability of yellow spinning a yellow section is 1/6.
A jar contains 25 pennies, 20 nickels, and 15 dimes. If someone picks one coin without looking, what are the chances that they will pick the following:
Question 13.
penny ______________
Answer:
\(\frac{5}{12}\),
Explanation:
Given that total no. of outcomes that jar contains are 25 + 20 + 15 = 60 and no. of penny are 25, so probability of penny is 25/60 = 5/12.
Question 14.
nickel ______________
Answer:
\(\frac{1}{3}\),
Explanation:
Given no. of nickel are 20 so probability of nickel is 20/60 = 1/3.
Question 15.
dime ______________
Answer:
\(\frac{1}{4}\),
Explanation:
Given that no. of dimes in jar are 15 so probability of dime is 15/60 = 1/4.