Multiplication of a Matrix by a Number – Definition, Properties, Examples | How to Multiply a Matrix by a Number?

If you are struggling with the topic Multiplication of a Matrix by a Number then this is the right place. If the matrix A is multiplied by k, then the output matrix is kA in which all the elements are k times the elements of A. You must multiply every element of matrix A by the number. As we multiply the matrix with the number, the order of the matrix will not change. The multiplication of a matrix by a number does not depend on the order of the matrix.

Therefore, check out the matrix and multiply it with the given number. The output matrix order is the same as the given matrix multiplied by the number.

What is Multiplication of a Matrix by a Number?

The Matrix Multiplication by a number is finding the product of the matrix by a number. Every element of the matrix is multiplied by the given number to find the output of the Multiplication of a Matrix by a Number. We will not consider the order of the matrix while multiplying the matrix by a number. If A = aij_{m × n} where (i, j)th element and m number of rows and n number of columns and k is the scalar or number, then the multiplication becomes

k × A = kA
If A = aij_{m × n}, kA = k aij_{m × n}

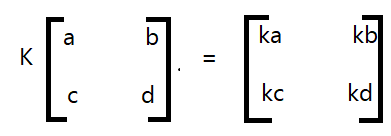
where k is the scalar and A is the matrix.

Properties of Multiplication of a Number by a Matrix

The below properties belong to Scalar Multiplication of a Matrix and helps you to know how to multiply a matrix by a number. Let us consider two matrices A = [aij] and B = [bij] which are having the same order as m × n and also k and l are scalars, then

• 1A = A, where 1 is the identity element of a matrix and A is the matrix.
• kO_{m, n} = O_{m, n}
• 0A = O_{m, n}
• k(pA) = (kp)A
• (k + l)A = kA + lA
  Proof: Substitute A = [aij] in (k + l)A
  (k + l)A = (k + l)[aij]
  = [(k + l)aij] + [kaij] + [laij]
  = k[aij] + l[aij]
  = kA + lA
  (k + l)A = kA + lA
• k(A + B) = kA + kB,
  Proof: Substitute A = [aij] and B = [bij] in k (A + B).
  k (A + B) = k ([aij] + [bij])
  = k[aij + bij] = [k(aij + bij)] = [(kaij) + (kbij)]
  = [kaij] + [kbij] = k[aij] + k[bij] = kA + kB
  k(A + B) = kA + kB,

Also, Read:

• Addition of Matrices
• Subtraction of Matrices

Multiplying a Matrix by a Number Examples

Example 1. If \( A =\left[
\begin{matrix}
12&4 \cr
6&10 \cr
\end{matrix}
\right]
\) and k = 1, then find kA?

Solution: The given matrix is \( A =\left[
\begin{matrix}
12&4 \cr
6&10 \cr
\end{matrix}
\right]
\) and k = 1.
To find kA, we need multiply the value of k with all the elements of the matrix A.
Now, multiply all the elements of the matrix A with 1.
\( kA = (1) \left[
\begin{matrix}
12&4 \cr
6&10 \cr
\end{matrix}
\right]
\) = \( \left[
\begin{matrix}
1 * 12&1 * 4 \cr
1 * 6&1 * 10 \cr
\end{matrix}
\right]
\) = \( \left[
\begin{matrix}
12&4 \cr
6&10 \cr
\end{matrix}
\right]
\)

Therefore, the multiplication of k and A is \( \left[
\begin{matrix}
12&4 \cr
6&10 \cr
\end{matrix}
\right]
\)

Example 2. If \( A =\left[
\begin{matrix}
10&2&11 \cr
5&6&4 \cr
1&0&3 \cr
\end{matrix}
\right]
\) and c = -2, then find cA?

Solution: The given matrix is \( A =\left[
\begin{matrix}
10&2&11 \cr
5&6&4 \cr
1&0&3 \cr
\end{matrix}
\right]
\) and c = -2.
To find cA, multiply the value of c by all the elements of matrix A.
Now, multiply all the elements of the matrix A with -2 to find the output.
\( cA = (-2)\left[
\begin{matrix}
10&2&11 \cr
5&6&4 \cr
1&0&3 \cr
\end{matrix}
\right]
\) = \( \left[
\begin{matrix}
-2 * 10&-2 * 2&-2 * 11 \cr
-2 * 5&-2 * 6&-2 * 4 \cr
-2 * 1&-2 * 0&-2 * 3 \cr
\end{matrix}
\right]
\) = \( \left[
\begin{matrix}
-20&-4&-22 \cr
-10&-12&-8 \cr
-2&0&-6 \cr
\end{matrix}
\right]
\)

Therefore, the multiplication of c and A is \( \left[
\begin{matrix}
-20&-4&-22 \cr
-10&-12&-8 \cr
-2&0&-6 \cr
\end{matrix}
\right]
\)

Example 3. Find 3B where \( B =\left[
\begin{matrix}
4&5 \cr
11&10 \cr
\end{matrix}
\right]
\)

Solution: the given matrix is \( B =\left[
\begin{matrix}
4&5 \cr
11&10 \cr
\end{matrix}
\right]
\)
To find 3B, we need to multiply the value of 3 by all the elements of matrix B.
\( 3B =\left[
\begin{matrix}
3 * 4&3 * 5 \cr
3 * 11&3 * 10 \cr
\end{matrix}
\right]
\) = \( \left[
\begin{matrix}
12&15 \cr
33&30 \cr
\end{matrix}
\right]
\)

Therefore, the required matrix is 3B = \( \left[
\begin{matrix}
12&15 \cr
33&30 \cr
\end{matrix}
\right]
\)

Example 4. Find 5A – 2B where \( A =\left[
\begin{matrix}
1&0 \cr
0&1 \cr
\end{matrix}
\right]
\) and \( B =\left[
\begin{matrix}
3&4 \cr
2&7 \cr
\end{matrix}
\right]
\)

Solution: Given matrices are \( A =\left[
\begin{matrix}
1&0 \cr
0&1 \cr
\end{matrix}
\right]
\) and \( B =\left[
\begin{matrix}
3&4 \cr
2&7 \cr
\end{matrix}
\right]
\)
Firstly, find 5A.
To find 5A, we need to multiply the value 5 with all the elements of matrix A.
\( 5A =\left[
\begin{matrix}
5 * 1&5 * 0 \cr
5 * 0&5 * 1 \cr
\end{matrix}
\right]
\) = \( \left[
\begin{matrix}
5&0 \cr
0&5 \cr
\end{matrix}
\right]
\)
Now, find 2B.
\( 2B =\left[
\begin{matrix}
2 * 3&2 * 4 \cr
2 * 2&2 * 7 \cr
\end{matrix}
\right]
\) = \( \left[
\begin{matrix}
6&8 \cr
4&14 \cr
\end{matrix}
\right]
\)
Finally, find 5A – 2B = \( \left[
\begin{matrix}
5&0 \cr
0&5 \cr
\end{matrix}
\right]
\) – \( \left[
\begin{matrix}
6&8 \cr
4&14 \cr
\end{matrix}
\right]
\)
\( \left[
\begin{matrix}
5 – 6&0 – 8 \cr
0 – 4&5 – 14 \cr
\end{matrix}
\right]
\) = \( \left[
\begin{matrix}
-1&-8 \cr
-4&-9 \cr
\end{matrix}
\right]
\)

Therefore, the value of 5A – 2B = \( \left[
\begin{matrix}
-1&-8 \cr
-4&-9 \cr
\end{matrix}
\right]
\)

FAQs on Matrix Multiplication by a Number

1. How to do Matrix Multiplication by a Number?

Multiply each element of th ematrix by a number.

2. Does the Multiplication of Matrix by a Number depends on the order of the matrix?

No, the order of the matrix will not affect the Matrix Multiplication by a Number.

3. Write any two properties of Scalar Multiplication of a Matrix.

The two properties of Scalar Multiplication of a Matrix are

• (k + l)A = kA + lA
• k(A + B) = kA + kB

4. Is it possible to multiply a matrix by more than one number?

Yes, you can multiply a matrix by more than one number.

5. Find 3A where \( A = \left[
\begin{matrix}
1&0 \cr
0&1 \cr
\end{matrix}
\right]
\)

The answer is \( 3A = \left[
\begin{matrix}
3&0 \cr
0&3 \cr
\end{matrix}
\right]
\)

Summary

Be the first to learn all the 10th Grade Math Matrices concepts on our website. If you want the best way of learning, you must go through our articles, worksheets, and practice tests, etc. Every article we provide here will give you the best practice and improve your knowledge.