Scalar Multiplication of a Matrix will define the output of a matrix when it is multiplied by a scalar. The Multiplication of matrices by a scalar is nothing but multiplying a matrix with real numbers. The real number is multiplied by every element of the matrix. In other words, the entire matrix is multiplied by the real number without missing any element in it. Let us find the product of a real number and a matrix in the 10th Grade Math Scalar Multiplication of a Matrix article. Every example will let you know how to multiply a matrix by a scalar.
What is Scalar Multiplication of Matrices?
The Scalar Multiplication of Matrices is finding the product of the matrices and a scalar. In scalar multiplication, we multiply every element of the matrix by a real number. If you consider a matrix A which is equal to aij and the scalar k, then the multiplication of matrices by a scalar becomes kA = kaij.
k × A = kA = kaijm × n where m and n are numbers of rows and number of columns of the given matrix.
Here kA is the matrix obtained from the multiplication of scalar k and Matrix A.
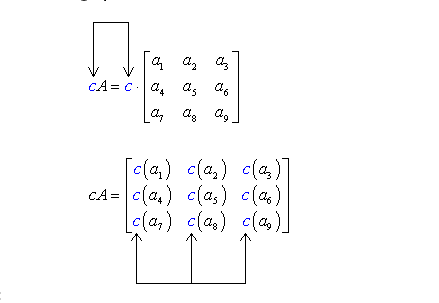
where c is the scalar and A is the matrix.
Also, find
- Identity (or Unit) Matrix
- Triangular Matrix
- Order of a Matrix
- Addition of Two Matrices
- Subtraction of Two Matrices
- Equal Matrices
- Null Matrix
Properties of Scalar Multiplication of a Matrix
Check out the different properties of scalar multiplication of a matrix when one or more than one matrices are given. If you take two matrices A = [aij] and B = [bij] which are having the same order as m × n and also k and l are scalars, then
-
- k(A + B) = kA + kB,
Proof: Substitute A = [aij] and B = [bij] in k (A + B).
k (A + B) = k ([aij] + [bij])
= k[aij + bij] = [k(aij + bij)] = [(kaij) + (kbij)]
= [kaij] + [kbij] = k[aij] + k[bij] = kA + kB
k(A + B) = kA + kB, - (k + l)A = kA + lA
Proof: Substitute A = [aij] in (k + l)A
(k + l)A = (k + l)[aij]
= [(k + l)aij] + [kaij] + [laij]
= k[aij] + l[aij]
= kA + lA
(k + l)A = kA + lA - k(pA) = (kp)A
- 0A = Om, n
- kOm, n = Om, n
- 1A = A, where 1 is the identity element of a matrix.
- k(A + B) = kA + kB,
Solved Examples on Matrix Multiplication by a Scalar
Scalar Multiplication of a Matrix solved examples are provided below with step by step explanation. Check out the answers and solving process to learn to solve Scalar Multiplication of Matrices problems.
Example 1. If \( A =\left[
\begin{matrix}
6&2 \cr
3&5 \cr
\end{matrix}
\right]
\) and k = 2, then find kA?
Solution: The given matrix is \( A =\left[
\begin{matrix}
6&2 \cr
3&5 \cr
\end{matrix}
\right]
\) and k = 2.
To find kA, we need multiply the value of k with all the elements of the matrix A.
Now, multiply all the elements of the matrix A with 2.
\( kA = (2) \left[
\begin{matrix}
6&2 \cr
3&5 \cr
\end{matrix}
\right]
\) = \( \left[
\begin{matrix}
2 * 6&2 * 2 \cr
2 * 3&2 * 5 \cr
\end{matrix}
\right]
\) = \( \left[
\begin{matrix}
12&4 \cr
6&10 \cr
\end{matrix}
\right]
\)
Therefore, the multiplication of k and A is \( \left[
\begin{matrix}
12&4 \cr
6&10 \cr
\end{matrix}
\right]
\)
Example 2. If \( A =\left[
\begin{matrix}
5&1&5 \cr
4&9&3 \cr
0&5&4 \cr
\end{matrix}
\right]
\) and c = -3, then find cA?
Solution: The given matrix is \( A =\left[
\begin{matrix}
5&1&5 \cr
4&9&3 \cr
0&5&4 \cr
\end{matrix}
\right]
\) and c = -3.
To find cA, we need to multiply the value of c by all the elements of matrix A.
Now, multiply all the elements of the matrix A with -3 to find the output.
\( cA = (-3)\left[
\begin{matrix}
5&1&5 \cr
4&9&3 \cr
0&5&4 \cr
\end{matrix}
\right]
\) = \( \left[
\begin{matrix}
-3 * 5&-3 * 1&-3 * 5 \cr
-3 * 4&-3 * 9&-3 * 3 \cr
-3 * 0&-3 * 5&-3 * 4 \cr
\end{matrix}
\right]
\) = \( \left[
\begin{matrix}
-15&-3&-15 \cr
-12&-27&-9 \cr
-0&-15&-12 \cr
\end{matrix}
\right]
\)
Therefore, the multiplication of c and A is \( \left[
\begin{matrix}
-15&-3&-15 \cr
-12&-27&-9 \cr
-0&-15&-12 \cr
\end{matrix}
\right]
\)
Example 3. Find 4B where \( B =\left[
\begin{matrix}
1&0 \cr
0&1 \cr
\end{matrix}
\right]
\)
Solution: the given matrix is \( B =\left[
\begin{matrix}
1&0 \cr
0&1 \cr
\end{matrix}
\right]
\)
To find 4B, we need to multiply the value of 4 by all the elements of matrix B.
\( 4B =\left[
\begin{matrix}
4 * 1&4 * 0 \cr
4 * 0&4 * 1 \cr
\end{matrix}
\right]
\) = \( \left[
\begin{matrix}
4&0 \cr
0&4 \cr
\end{matrix}
\right]
\)
Therefore, the required matrix is 4B = \( \left[
\begin{matrix}
4&0 \cr
0&4 \cr
\end{matrix}
\right]
\)
Example 4. Find 3A – 2B where \( A =\left[
\begin{matrix}
4&5 \cr
3&2 \cr
\end{matrix}
\right]
\) and \( B =\left[
\begin{matrix}
6&7 \cr
4&2 \cr
\end{matrix}
\right]
\)
Solution: Given matrices are \( A =\left[
\begin{matrix}
4&5 \cr
3&2 \cr
\end{matrix}
\right]
\) and \( B =\left[
\begin{matrix}
6&7 \cr
4&2 \cr
\end{matrix}
\right]
\)
Firstly, find 3A.
To find 3A, we need to multiply the value 3 with all the elements of matrix A.
\( 3A =\left[
\begin{matrix}
3 * 4&3 * 5 \cr
3 * 3&3 * 2 \cr
\end{matrix}
\right]
\) = \( \left[
\begin{matrix}
12&15 \cr
9&6 \cr
\end{matrix}
\right]
\)
Now, find 2B.
\( 2B =\left[
\begin{matrix}
2 * 6&2 * 7 \cr
2 * 4&2 * 2 \cr
\end{matrix}
\right]
\) = \( \left[
\begin{matrix}
12&14 \cr
8&4 \cr
\end{matrix}
\right]
\)
Finally, find 3A – 2B = \( \left[
\begin{matrix}
12&15 \cr
9&6 \cr
\end{matrix}
\right]
\) – \( \left[
\begin{matrix}
12&14 \cr
8&4 \cr
\end{matrix}
\right]
\)
\( \left[
\begin{matrix}
12 – 12&15 – 14 \cr
9 – 8&6 – 4 \cr
\end{matrix}
\right]
\) = \( \left[
\begin{matrix}
0&1 \cr
1&2 \cr
\end{matrix}
\right]
\)
Therefore, the value of 3A – 2B = \( \left[
\begin{matrix}
0&1 \cr
1&2 \cr
\end{matrix}
\right]
\)
Faqs on Scalar Multiplication of a Matrix
1. What is the scalar multiplication of a matrix?
The scalar multiplication of a matrix is the multiplication of a matrix by a real number. We can multiply each element of the matrix by a real number. If k is a scalar and A = aij, then kA = kaij.
2. Is it possible to multiply a matrix by more than one scalar?
Yes, we can multiply a single matrix by more number of matrices.
3. If scalar k = 1 and matrix is an identity matrix, what is the multiplication of a matrix by a scalar.
The multiplication of the identity matrix and 1 becomes the identity matrix.
4. Find 2A where \( A = \left[
\begin{matrix}
2&4 \cr
6&8 \cr
\end{matrix}
\right]
\)
The answer is \( 2A = \left[
\begin{matrix}
4&8 \cr
12&16 \cr
\end{matrix}
\right]
\)
Conclusion
The Scalar Multiplication of Matrix examples and properties are given in this article. You can stay connected to our website to know the latest syllabus of all the topics. We will give you the best opportunity to learn online and offline using our articles. You can use our website in both ways to learn all the difficult concepts. So, don’t wait. Immediately start preparing for the exam and get good marks.
