Angle is one of the most important concepts in Mathematics. Students who feel tough & tricky to understand the concept of Measuring an Angle can go through this article. As we have explained clearly about how to measure angles easily. Usually, the subject of trigonometry is based on the Measurement of Angles.
Learning Geometry concepts is most important to all students as it covers various concepts like angles. In this article, you will find precise info regarding how to measure an angle in degrees, Measuring an Angle by a Protractor, without a protractor that helps for better understanding of the topic.
Also Check:
What is an Angle?
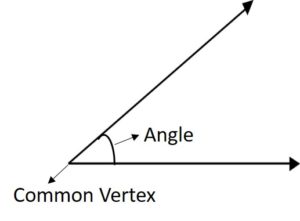
In geometry, an angle can be described as the figure formed when two rays are joined together or intersect at a single point. The point where two rays coincide is called the vertex of an angle. Angles are measured in degrees and angle is denoted by the symbol ∠ . Let’s take a glance at how the angle looks:
Measuring an Angle with a Protractor
Generally, we use a ruler for measuring the line segment of a length but the angles are measured with the commonly used geometry equipment called Protractor. An angle is measured in degrees and will denote with a symbol °.
A protractor has 360 degrees and it is one complete revolution. It is a semi-circular tool in geometry used to measure and draw angles. There are two sets of measurements in the protractor, one is the clockwise direction from 0° to 180° and another an anti-clockwise direction from 180° to 0°.
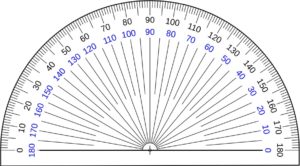
If the kids are familiar with this tool then it will be easy for them to measure or construct an angle using a protractor. While using the protractor, the students should know where the common vertex line hits the protractor.
The size of an angle depends on how wide the two sides are opening. The following figure explains how we measure an angle with a common vertex.
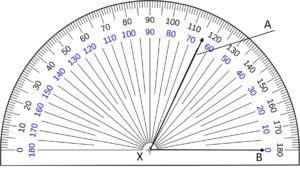
In the above figure, the angle AXB i.e., ∠AXB = 65°.
How to Measure an Angle without a Protractor?
When you don’t have a protractor handy, you can define the angle size with the help of basic geometric principles of the triangle. The calculation of measuring an angle without a protractor can rely on whether you’re measuring an acute, obtuse, or reflex angle. Check the below steps of all three methods carefully and perform the angle measurements easily & effortlessly:
Method 1: Acute
- Firstly, draw a vertical line connecting the 2 rays of the angle.
- Later, start measuring the length of the adjacent side to find the run.
- Then, do the same with the length of the opposite side to discover the rise.
- Now, divide rise by the run to determine the slope of the angle.
- Finally, make use of the calculator to find the degrees of the angle,
Method 2: Obtuse
- At first, extend the bottom ray of the angle in a straight line.
- Draw a vertical line connecting the top ray and the line.
- Next, measure the length of the bottom line from the vertex.
- After that, measure the length of the vertical line.
- Find the slope of the acute angle to determine the degrees of the acute angle.
- At last, subtract the degrees of the acute angle from 180° to find the actual measure of an angle.
Method 3: Reflex
- In step 1, you have to identify the smaller acute angle connected with the reflex angle.
- Now, draw a vertical line connecting the rays of the acute angle.
- Next, measure the rise and the run of the acute angle.
- Divide rise by a run to find the slope of the acute angle.
- Open the calculator and find the degrees of the acute angle.
- Subtract the degrees of the acute angle from 360°.
- In the end, you will get the degrees of the given angle.
A Comprehensive Collection of 4th Grade Math Activity Worksheets are readily available to print are for free and learn the Important Skills taught in your Classroom.
How to Measure Angles in Degrees?
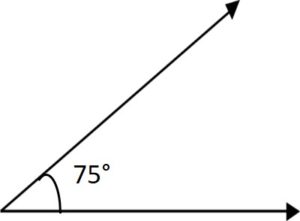
Generally, we measure angles in degrees. A degree is a measurement of a plane angle, which has 360 degrees in one full rotation. Angles can also be measured in radians but mostly, we use the degrees with the help of a protractor and it is one of the most common approaches to measure angles. We represent degrees by a small circle as ° following the measured number. For example, we represent 75 degrees as 75°.
Measuring Angles with a Protractor Examples
Example 1:
Draw an angle of 44° with the protractor.
Solution:
To draw an angle of 44° we go by step by step procedure.
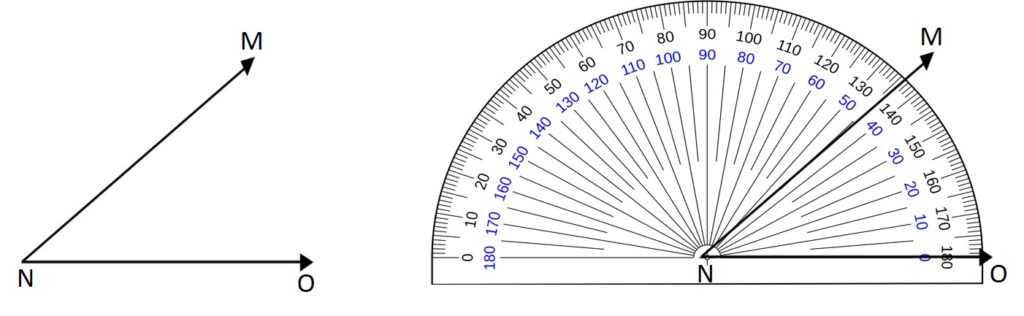
Firstly, we take an angle and name it ∠MNO.
Now, draw a line NO and keep the protractor on the line drawn. So, that the midpoint of the protractor is at point N.
Adjust the protractor where the line NO is parallel to the straight edge of the protractor.
The protractor has two way of measurements marked from 0° to 180° from both ends.
Mark the point where the point NO coincides with the 0°.
Now, from 0°, check the ray that NM matches with the curved edges of the protractor. This expression gives us the measurement of an angle ∠MNO.
The picture representation of an angle ∠MNO is as follows:
Example 2:
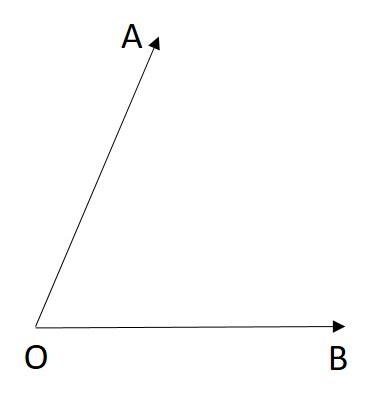
Measure the given angle AOB in degrees.
Solution:
First, observe the given angle ∠AOB.
We measure an angle in degrees by using a protractor.
Place the protractor on the baseline and the midpoint of the protractor should be at point O.
Change the position of the protractor where the line OB is a straight edge to the protractor.
Now, measure the angle from 0° where the line OB coincides.
Check the degrees of the ray OA that coincides with the edges of the protractor. The ray where it coincides is our degree’s measurement of an angle.
Let us see how many degrees is our angle ∠AOB from the image given below:
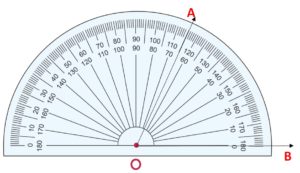
Thus, the ∠AOB is 65°.
Example 3:
Measure an angle ∠QPR in a clockwise direction of a protractor.
Solution:
First, take an angle ∠QPR.
Keep the protractor on baseline RP and the midpoint of the protractor be at point P.
The line PR should be the straight edge to the protractor.
Next, measure the angle from 0° to 180° where it coincides with the line PR.
Read the protractor where the line QP coincides with the degrees of a scale and it is our measurement of an angle ∠QPR.
The image gives a clear representation of how the angel ∠QPR was placed in a protractor and measured.
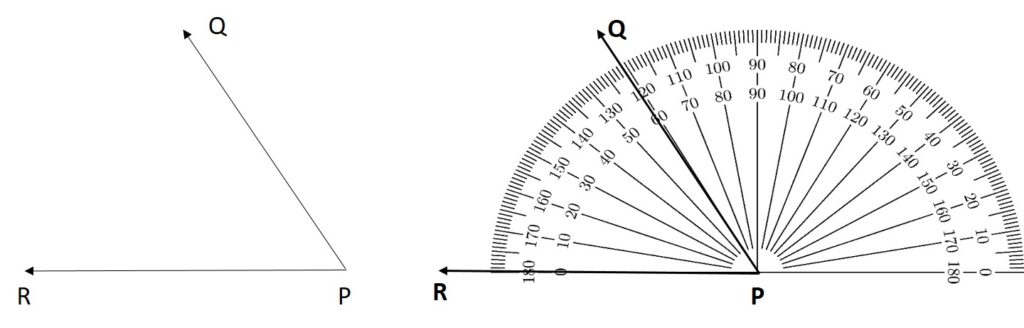
So, the ∠QPR is equal to 59°.
