Many students get confused with these three terms mean, median, and mode. In this article, we can easily learn these three terms without any confusion, but first, we are learning the mean in this article with more knowledge. In Mathematics, a mean is just defined because of the average of the given set of numbers. The mean is additionally considered together with the measures of central tendencies in Statistics. Mean gives the central value of the set of values. The remaining two measures of central tendency are median and mode.
Do Read:
Mean – Introduction
Let us discuss the definition of the mean, formula with an example. To calculate the mean, we need to add the total values in a datasheet and then divide the sum by the total number of values. Consider an example, we want to find the average age of students in a class, then we have to add the age of each student present in the class and then the sum result is divided by the total number of students present in the class.
Mean is commonly used in statistics. In school, we have to learn this concept with the name average. But in the higher classes, we will learn this topic by name mean, it is an advanced version of a series or sequence of a number. We will also learn about the median and mode along with the mean. Mode is defined as the number in the list, which is repeated a more number of times. Median is defined as the middle value of a given data when all the values are arranged in ascending order.
What is meant by Mean?
The mean is defined because of the average or the common value in a collection of numbers. In statistics, it is a measure of the central tendency of a probability distribution along median and mode. Mean denotes the equal distribution of values for a given data set.
The mean meaning is to evaluate the average. Mean is that the sum of all the given data divided by the general or total number of data values given within the set. The formula for mean calculation is given by,
Mean is =sum of the observations / Total number of the Observations.
Usually, the symbol of the mean is ‘X̄’ Therefore bar of x is the mean representation. so, it will be
X̄ = (x1 + x2 + x3 +….+xn)/n.
Types of Mean
The mean has three different types. There are:
- Arithmetic Mean (AM)
- Harmonic Mean (HM)
- Geometric Mean (GM)
Arithmetic Mean: The arithmetic mean is defined as the simplest and most widely used to measure average or mean. The sum of a group of numbers, and then divided that sum by the total numbers used in the series.
For example, given data is 1, 2, 3, 4, 5, 6 then the arithmetic mean is
(1+ 2+ 3+ 4+ 5+ 6 )/6 = 21/6 = 3.5
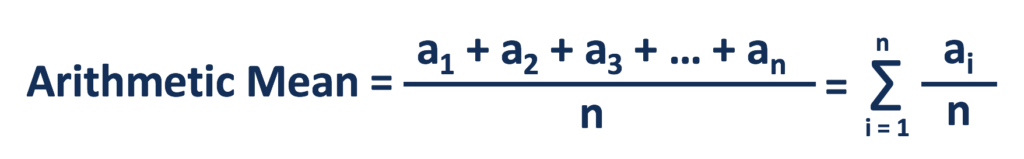
Harmonic Mean: The Harmonic mean is defined as the average ratio. If two numbers x and y, then the harmonic mean is 2xy(x+y). If we have three elements then the harmonic mean is 3xyz(xy+xz+yz).
Harmonic Mean (HM) = n / (1/x1+ 1/x2+ 1/x3+……..1/xn).
Geometric Mean: The Geometric mean is defined as, multiplying all the numbers together and taking the nth root of the product.
Mean of Raw Data
The mean of raw data is to calculate, first take the sum of all the raw data into samples and then divide them by the total number of raw data in the sample. Then we will divide by the total number of the raw data points. This will also be called ‘n’ for sample size.
In the mean of raw data n is the observations, to calculate the arithmetic mean a set of data we will first add (sum) all values (x), and then divide the result by the number of values (n). ∑ is the symbol used to summation indication of values. so we obtained a formula of the mean (x̄) is as given below:
x̄=∑ x/n
If x1, x2, x3, ……. xn are there. where ‘n ‘ is observations, then
Arithmetic Mean = (x1, x2, x3, ……. xn)/n = (∑xi)/n ,Where ∑ (Sigma) is a Greek letter showing summation.
Mean of Grouped Data
The mean of grouped data is to calculate, first will determine the midpoint or class mark of each class or interval. These classmarks or midpoints must be multiplied by the frequencies of the corresponded classes. In the mean of grouped data, the sum of the products divided by the entire number of values is going to be the worth (or) value of the mean.
In grouped data, the mean uses the class intervals of the midpoints. So, the formula of grouped data mean is,
Mean = Sum of the (Midpoint x Frequency) Sum of Frequency.
How to Find Mean?
For finding the mean we have steps to calculate the mean value of a given data. The process is
- First, we add all the numbers, then the result is called the sum.
- Next, we can count the given data numbers. This number is called a sample size.
- After that sum is divided by the total number of given values.
Mean of Negative Numbers
Till now we have seen how to find the mean of the positive number but if we want to find the mean of a negative number. Let us see how to find them,
Example:
1. Find the mean of 6, -3, 9, -7, 2, 1.
Solution:
Given the data set is 6, -3, 9, -7, 2, 1
We find the mean of a given data,
The formula of Mean is,
Mean = Sum of data / Total number of data.
Substitute the given values in the above formula, we get
Mean = ( 6 + (-3) + 9 + (-7) +2 + 1) / 6
Mean = (6- 3 + 9 -7 +2 + 1) / 6
Mean = 8/ 6 = 1.33
Therefore, the mean of a given data is 1. 33
Solved Examples on Mean of Grouped and Raw Data
Problem 1:
Calculate the mean of the given data 3, 5, 7, 9?
Solution:
Given data values are 3, 5, 7, 9
The total number of given data value is 4
Now, we can be finding the Mean of the given value.
We know, the formula of Mean.
Mean = Sum of data / Total number of the data
Substitute the given values into the above formula, we get
Mean = (3+5+7+9)/4 = 24/4 = 6
Therefore the Mean of the given data is 6.
Problem 2:
Find the mean of the first 10 even numbers?
Solution:
Given, find the 10 even numbers mean
Even numbers of first 10 numbers are 2, 4, 6, 8, 10
Now we finding the mean of the above even numbers.
The total number of data is 5
We know the Mean formula,
Mean = Sum of data set / Total number of data set
Substitute the values in the above formula, we get
Mean = (2+4+6+8+10) / 5 = 30/5 = 6
Therefore, the Mean of the first 10 even numbers is 6.
Problem 3:
If X is added to the given data set 4, 6, 8, 12, 5 and the new mean is 10. Calculate the value of X?
Solution:
Given the data set is 4, 6, 8, 12, 5 and the new mean is 10.
We are finding the value of X.
The total of the given data set is 5.
We know the mean formula, which is
Mean = sum of data / total number of data.
Substitute the given values into the above formula, we get
15 = (4+ 6+ 8+ 12+ 5+ X)/ 5
Simplify it, we get the value of X.
15 x 5 = 35+ X
75 = 35 + X
Subtract the value we get
75 – 35 = X
X = 40
Therefore the value of X is 40.
Problem 4:
Find the value of x. If the mean of five observations x, x + 3, x + 5, x + 7, x + 9 is 1.
Solution :
Given the mean of five observations x, x + 3, x + 5, x + 8, x + 9 is 10.
Sum the given five observations,
Sum = x + (x + 3) + (x + 5) + (x + 8) + (x + 9) = 5x + 25
Now, we find the mean.
We know the mean formula,
Mean = sum of observations/ Total number of observations.
10 = ( 5x + 25 ) / 5
10 x 5 = 5x + 25
50 – 25 = 5x
25 = 5x
x =5
Therefore, the value of x is 5.
Frequently Asked Questions on Mean
1. Define Mean?
Mean is defined as the ratio of the sum of all the observations or data and the total number of observations or data set in statistics. The formula for mean calculation is,
Mean = Sum of all the observations / Total number of the observations.
2. What are the types of Mean?
There are three different types of Mean, namely:
- Arithmetic Mean (AM)
- Geometric Mean (GM)
- Harmonic Mean (HM)
3. What is the purpose of Mean?
The main purpose of mean in statistics is preferred by the average, it is most commonly used to measure the center of a numerical data set. The Sum of all the values is divided by the total number of values is called as Mean.
4. How is Mean calculated?
The mean of a given data calculation process is as given below:
- Add all the numbers, the result is called the sum.
- After adding the sum is divisible by the total numbers of the given data.
5. List the merits of Mean?
The advantages of Mean is listed below:
- It is simple to understand and easily calculate.
- Mean is based on all observations of the given data.
- It is suitable for further algebraic functions.
- Mean is widely used in statistical analysis and it is capable of being treated mathematically.
- Mean is the fluctuation of sampling.
- Every kind of data that is mean can be calculated.