All the solutions provided in McGraw Hill Math Grade 5 Answer Key PDF Chapter 10 Lesson 9 Division with Unit Fractions will give you a clear idea of the concepts.
McGraw-Hill My Math Grade 5 Answer Key Chapter 10 Lesson 9 Division with Unit Fractions
Build It
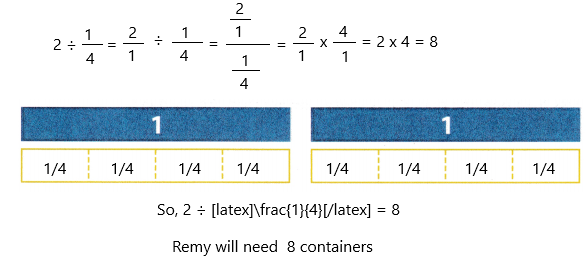
Remy has 2 gallons of lemonade. She needs to divide the lemonade into \(\frac{1}{4}\)-gallon containers. How many \(\frac{1}{4}\)-gallon containers does she need?
Find 2 ÷ \(\frac{1}{4}\) ← THINK: How many groups of \(\frac{1}{4}\) are in 2?
1. Represent the 2 gallons by placing 2 whole fraction tiles.
2. Place enough of the \(\frac{1}{4}\)-fraction tiles below the 2 whole fraction tiles to represent the same amount. Label the model with \(\frac{1}{4}\)-fraction tiles.

How many \(\frac{1}{4}\)-fraction tiles did it take to equal the 2 whole fractions tiles?
So, 2 ÷ \(\frac{1}{4}\) = ____
Remy will need ____ containers.
Answer:
The number of gallons of lemonade = 2
2 ÷ 1/4
if we divide
Try it
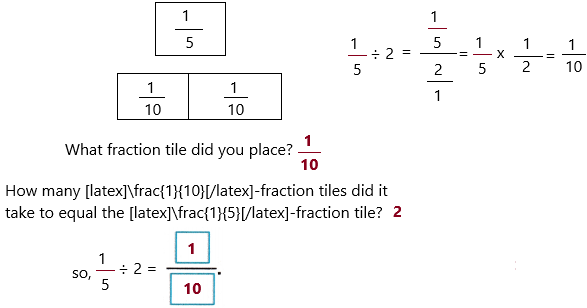
Find \(\frac{1}{5}\) ÷ 2.
Helpful Hint
\(\frac{1}{5}\) represents one out of the five tiles that would make a whole.
2. Since you are dividing by 2, you are dividing \(\frac{1}{5}\) into two equal groups.
Find a fraction tile that when placed twice, will be the same size as the \(\frac{1}{5}\)-fraction tile.
Label the model with the fraction tiles you placed.
What fraction tile did you place? ____
How many \(\frac{1}{10}\)-fraction tiles did it take to equal the \(\frac{1}{5}\)-fraction tile? ____
So, \(\frac{1}{5}\) ÷ 2 =  ?
?
Answer:
Talk About It
Mathematical PRACTICE 2 Reason Determine whether each of the following statements is true or false. Explain your reasoning.
Question 1.
When a whole number greater than one is divided by a unit fraction less than one, the quotient is always greater than the dividend.
Answer: True
Explanation: you are dividing the whole number into fractional groups. So the quotient is always greater than the dividend.
Question 2.
When a unit fraction less than one is divided by a whole number greater than one, the quotient is always greater than the dividend.
Answer: False
Explanation: you are dividing a fraction into equal groups. So the quotient is always less than the dividend.
Practice It
Mathematical PRACTICE 5 Use Math Tools Use fraction tiles to divide. Draw your models below.
Question 3.
3 ÷ \(\frac{1}{3}\) = ___
Answer:
The above-given:
3 ÷ 1/3
Now dividing a whole number with a fraction number can be easily done by following a few simple steps that are below-mentioned.
1. Initially, we need to convert the given whole numbers into a fraction so that we can easily divide both fractions, so to do this we have to simply add 1 as the denominator.
2. After doing so we have to find the reciprocal for the obtained fraction number.
3. Now, that we have both the factions we need to multiply them with each other.
4. Finally, we can simplify the obtained equation to get its lowest terms.
procedure:
1. We need to represent the tiles that would make the whole.
2. Since you are dividing by 3, you are dividing \(\frac{1}{3}\) into three equal groups.
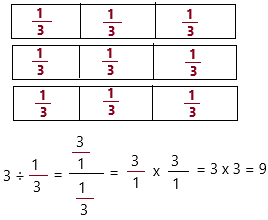
Therefore, 3 ÷ \(\frac{1}{3}\) = 9
Question 4.
2 ÷ \(\frac{1}{5}\) = ___
Answer:
The above-given:
2 ÷ 1/5
1. We need to represent the tiles that would make the whole.
2. Since you are dividing by 2, you are dividing \(\frac{1}{5}\) into five equal groups.
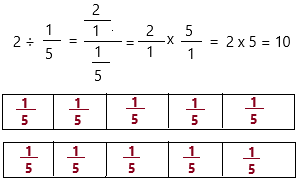
Therefore, 2 ÷ \(\frac{1}{5}\) = 10.
Question 5.
4 ÷ \(\frac{1}{2}\) = ___
Answer:
The above-given:
4 ÷ 1/2
1. We need to represent the tiles that would make the whole.
2. Since you are dividing by 4, you are dividing \(\frac{1}{2}\) into two equal groups.
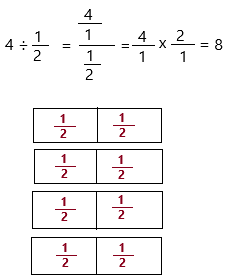
Therefore, 4 ÷ \(\frac{1}{2}\) = 8.
Question 6.
3 ÷ \(\frac{1}{6}\) = ___
Answer:
The above-given:
3 ÷ 1/6
1. We need to represent the tiles that would make the whole.
2. Since you are dividing by 3, you are dividing \(\frac{1}{6}\) into six equal groups.
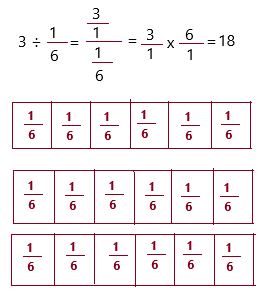
Therefore, 3 ÷ \(\frac{1}{6}\) = 18.
Question 7.
\(\frac{1}{3}\) ÷ 4 = ___
Answer:
The above-given:
1/3 ÷ 4
1. We need to represent the tiles that would make the whole.
2. Since you are dividing by 4, you are dividing \(\frac{1}{3}\) into four equal groups.
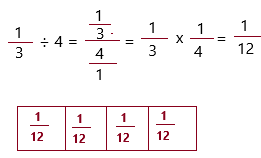
Therefore, \(\frac{1}{3}\) ÷ 4 = 1/12.
Question 8.
\(\frac{1}{2}\) ÷ 3 = ___
Answer:
The above-given:
1/2 ÷ 3
1. We need to represent the tiles that would make the whole.
2. Since you are dividing by 3, you are dividing \(\frac{1}{2}\) into three equal groups.
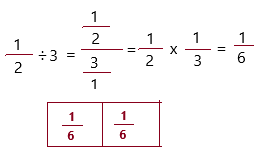
Therefore, \(\frac{1}{2}\) ÷ 3 = 1/6.
Question 9.
\(\frac{1}{3}\) ÷ 2 = ___
Answer:
The above-given:
1/3 ÷ 2
1. We need to represent the tiles that would make the whole.
2. Since you are dividing by 2, you are dividing \(\frac{1}{3}\) into two equal groups.
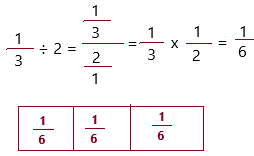
Therefore, \(\frac{1}{3}\) ÷ 2 = 1/6
Question 10.
\(\frac{1}{4}\) ÷ 2 = ___
Answer:
The above-given:
1/4 ÷ 2
1. We need to represent the tiles that would make the whole.
2. Since you are dividing by 2, you are dividing \(\frac{1}{4}\) into two equal groups.
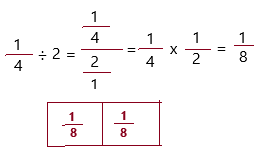
Therefore, \(\frac{1}{4}\) ÷ 2 = 1/8
Apply It
Question 11.
Mathematical PRACTICE 5 Use Math Tools Randall Is cutting a submarine sandwich into smaller pieces. He has 4 feet of sandwich that he wants to divide into \(\frac{1}{3}\)-foot sandwiches. How many sandwiches will he have after he cuts the sandwich? Use tiles to help you solve.
Answer:
The above-given:
According to the above-given information:
The equation would be:
4 ÷ 1/3
1. We need to represent the tiles that would make the whole.
2. Since you are dividing by 2, you are dividing \(\frac{1}{3}\) into three equal groups.
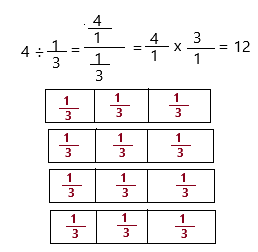
Therefore, he has 12 sandwiches after he cuts.
Question 12.
Brittany is making party favors. She is dividing \(\frac{1}{2}\) pound of jelly beans into 6 packages. How many pounds of jelly beans will be in each package? Use tiles to help you solve.

Answer:
According to the above-given information:
The equation would be:
1/2 ÷ 6
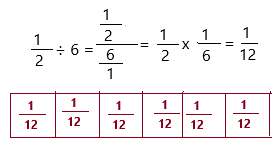
Therefore, 1/12 pounds of jelly beans will be in each package.
Question 13.
Mathematical PRACTICE 2 Use Symbols Circle the missing divisor below from the equation 5 ÷ ![]() = 25. Explain.
= 25. Explain.

Answer:
The above-given:
5 ÷ x = 25
we need to find out the x.
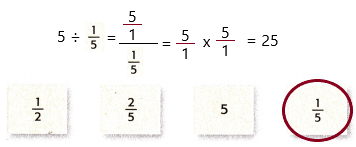
Question 14.
? Building on the Essential Question How can I use fraction tiles to help divide a whole number by a unit fraction?
Answer:
Fraction tiles can be used to help divide a whole number by a unit fraction.
– Fraction Tiles represent different fractions for instructive comparison. Expand the possibilities of teaching fractions and equivalence with proportionally sized tiles. They are used to teach students how to compare and construct fractions, work with mixed numbers, and add/subtract fractions with like and unlike denominators.
McGraw Hill My Math Grade 5 Chapter 10 Lesson 9 My Homework Answer Key
Practice
Use fraction tiles to divide. Draw your models below.
Question 1.
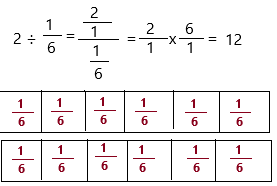
2 ÷ \(\frac{1}{6}\) = ____
Answer:
The above-given:
2 ÷ 1/6
Now dividing a whole number with a fraction number can be easily done by following a few simple steps that are below-mentioned.
1. Initially, we need to convert the given whole numbers into a fraction so that we can easily divide both fractions, so to do this we have to simply add 1 as the denominator.
2. After doing so we have to find the reciprocal for the obtained fraction number.
3. Now, that we have both the factions we need to multiply them with each other.
4. Finally, we can simplify the obtained equation to get its lowest terms.
procedure:
1. We need to represent the tiles that would make the whole.
2. Since you are dividing by 2, you are dividing \(\frac{1}{6}\) into six equal groups.
Question 2.
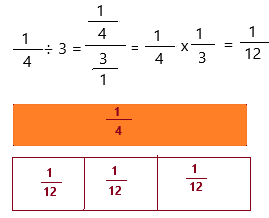
\(\frac{1}{4}\) ÷ 3 = ____
Answer:
Now dividing a whole number with a fraction number can be easily done by following a few simple steps that are below-mentioned.
1. Initially, we need to convert the given whole numbers into a fraction so that we can easily divide both fractions, so to do this we have to simply add 1 as the denominator.
2. After doing so we have to find the reciprocal for the obtained fraction number.
3. Now, that we have both the factions we need to multiply them with each other.
4. Finally, we can simplify the obtained equation to get its lowest terms.
procedure:
1. We need to represent the tiles that would make the whole.
2. Since you are dividing by 3, you are dividing \(\frac{1}{3}\) into three equal groups.
Problem Solving
Question 3.
Harold spent \(\frac{3}{4}\) hour milking cows. He milked 3 groups of cows. If he spent an equal amount of time on each group of cows, what fraction of an hour did he spend milking each group? Use tiles to help you solve.
Answer:
The above-given:
The time he spent milking cows = 3/4 hours.
The number of cows he milked for = 3
The equation: 3/4 ÷ 3
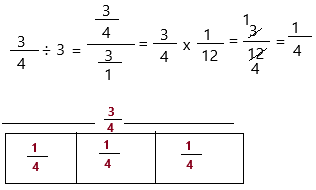
Therefore, he spent 1/4 hours milking each cow.
Question 4.
Rosanne and her family drove for 8 hours on their vacation trip. Every \(\frac{1}{2}\) hour, they played a different game. How many different games did they play? Use tiles to help you solve.
Answer:
The above-given:
The number of hours he drove = 8
The number of hours they played a different game = 1/2
The number of different games they played = P
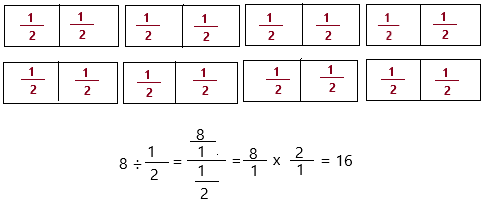
Therefore, they played 16 games.
Question 5.
Mathematical PRACTICE 5 Use Math Tools Girish used 4 cups of flour to make bread. He divided the flour into \(\frac{1}{3}\)-cup portions for each batch. How many batches of bread does Girish have? Use tiles to help you solve.
Answer:
The above-given:
The number of cups of flour used to make bread = 4
The number of portions for each bath divided = 1/3
The number of batches of bread Girish has = G
The equation would be:
4 ÷ 1/3
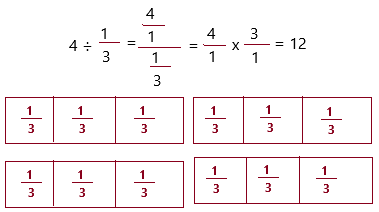
Therefore, he has 12 batches of bread.
Question 6.
Jason is cutting a roll of sausage into pieces that are \(\frac{1}{2}\)– inch thick. If the roll is 6 inches long, how many pieces of sausage can he cut? Use tiles to help you solve.

Answer:
The above-given:
The number of inches thick she cuts = 1/2
The number of inches = 6
The number of pieces of sausage can he cut = C
C = 6 ÷ 1/2
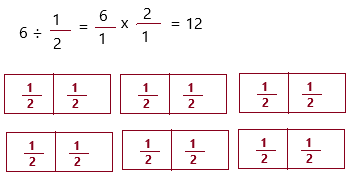
Therefore, he cuts it into 12 pieces.
Question 7.
Hubert cut a piece of yarn into pieces that are each \(\frac{2}{3}\) foot long. If the yarn is 6 feet long, how many pieces of yarn did he cut? Use tiles to help you solve.
Answer:
The above-given;
The length of each piece = 2/3 foot
The number of feet = 6
The number of pieces of yarn he can cut = Y
The equation:
Y = 6 ÷ 2/3
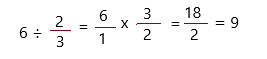
Therefore, he can cut the yarn into 9 pieces.