All the solutions provided in McGraw Hill My Math Grade 5 Answer Key PDF Chapter 10 Review will give you a clear idea of the concepts.
McGraw-Hill My Math Grade 5 Chapter 10 Review Answer Key
Vocabulary Check
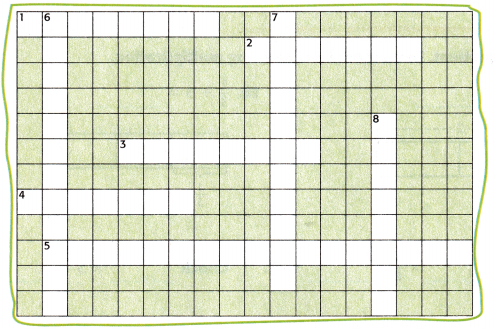
Read each clue. Fill the corresponding section of the crossword puzzle to answer each clue. Use the words In the word bank.
dividend divisor fraction Inverse operations
quotient mixed number scaling unit fraction
Across
1. The result of a division problem.
2. The number that divides the dividend.
3. A number that is being divided.
4. The process of resizing a number when you multiply by a fraction that is greater than or less than 1.
5. Operations that undo each other, such as multiplication and division.
Down
6. A fraction with a numerator of 1.
7. A number that has a whole number part and a fraction part.
8. A number that represents part of a whole or part of a set.
Answer:
1. the quotient is the number which is generated when we perform division operations on two numbers. Basically, it is the result of the division method.
Dividend = Quotient × Divisor + Remainder
If the remainder is equal to 0, then;
Dividend = Quotient × Divisor
Therefore,
Quotient = Dividend ÷ Divisor
2. In division, we divide a number by any other number to get another number as a result. So, the number which is getting divided here is called the dividend. The number which divides a given number is the divisor.
The operation of division in the form of Dividend ÷ Divisor = Quotient
The above expression can also be written as: Divisor = Dividend ÷ Quotient
– The divisor divides the number into parts.
– The divisor can divide the dividend either completely or partially. When divided completely, the remainder is zero and when divided partially, the remainder is a non-zero integer.
– Divisor could be a positive or negative number.
– A number that divides an integer exactly, leaving no remainder, is also termed the divisor.
– The divisor 1 and -1 can divide every integer, present in the number line.
3. In division, we divide a number by any other number to get another number as a result. So, the number which is getting divided here is called the dividend.
4. Scaling is the factor which is used to represent the object size. The size of the object can be shown by increasing or decreasing its original size. In general, the represented size of the object increased for the small object whereas it decreased for the bigger object. Scaling is used for better viewing of an object.
5. Inverse means the opposite effect of an action or a step. In mathematics, we have operations such as addition(+), subtraction(-), multiplication(x), division(÷), squaring, square root, and logarithms.
– When we use two operations together, it is possible to have an inverse impact on the result due to the operations used. The process in which the effect of one operation is inversed by another operation is termed as inverse operations.
6. All the fractions with 1 as the numerator are known as unit fractions. In these fractions, we take only one part of the whole which is divided equally into a finite number of parts. Unit denotes one. Therefore, they are known as unit fractions. Examples: 1/2, 1/3, 1/4…
7. A mixed number is a combination of a whole number and a proper fraction.
8. A fraction represents a numerical value, which defines the parts of a whole.

Concept Check
Estimate each product. Draw a bar diagram if necessary.
Question 9.
\(\frac{3}{4}\) × 23
______________
Answer:
The above-given equation:
3/4 x 23
The estimation of 23 is 24.
3/4 x 24
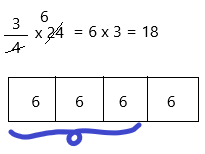
Therefore, the answer is 18.
Question 10.
\(\frac{1}{5}\) × 22
______________
Answer:
The above-given:
1/5 x 22
The estimation of 22 is 20.
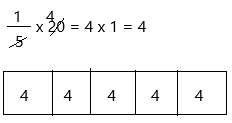
Therefore, the answer is 4.
Multiply. Write in the simplest form.
Question 11.
\(\frac{1}{3}\) × 21
______________
Answer:
Simplifying a fraction means reducing a fraction to its simplest form. A fraction is in its simplest form if its numerator and denominator have no common factors other than 1.
To simplify fractions, write the factors of the numerator and denominator and mark the common factors in them. Then, divide the numerator and denominator by the common factors until they have no common factor except 1. The fraction thus obtained is in its simplest form.
The above-given equation: 1/3 x 21
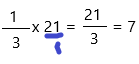
Therefore, \(\frac{1}{3}\) × 21 = 7.
Question 12.
26 × \(\frac{1}{2}\)
______________
Answer:
Simplifying a fraction means reducing a fraction to its simplest form. A fraction is in its simplest form if its numerator and denominator have no common factors other than 1.
To simplify fractions, write the factors of the numerator and denominator and mark the common factors in them. Then, divide the numerator and denominator by the common factors until they have no common factor except 1. The fraction thus obtained is in its simplest form.
The above-given equation: 26 x 1/2
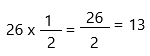
Therefore, 26 × \(\frac{1}{2}\) = 13
Question 13.
\(\frac{1}{5}\) × \(\frac{3}{8}\)
______________
Answer:
Simplifying a fraction means reducing a fraction to its simplest form. A fraction is in its simplest form if its numerator and denominator have no common factors other than 1.
To simplify fractions, write the factors of the numerator and denominator and mark the common factors in them. Then, divide the numerator and denominator by the common factors until they have no common factor except 1. The fraction thus obtained is in its simplest form.
The above-given equation: 1/5 x 3/8
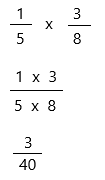
Therefore, \(\frac{1}{5}\) × \(\frac{3}{8}\) = 3/40
Question 14.
\(\frac{1}{2}\) × \(\frac{7}{8}\)
______________
Answer:
Simplifying a fraction means reducing a fraction to its simplest form. A fraction is in its simplest form if its numerator and denominator have no common factors other than 1.
To simplify fractions, write the factors of the numerator and denominator and mark the common factors in them. Then, divide the numerator and denominator by the common factors until they have no common factor except 1. The fraction thus obtained is in its simplest form.
The above-given equation: 1/2 x 7/8
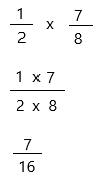
Therefore, \(\frac{1}{2}\) × \(\frac{7}{8}\) = 7/16.
Question 15.
3\(\frac{1}{4}\) × \(\frac{3}{5}\)
______________
Answer:
Simplifying a fraction means reducing a fraction to its simplest form. A fraction is in its simplest form if its numerator and denominator have no common factors other than 1.
To simplify fractions, write the factors of the numerator and denominator and mark the common factors in them. Then, divide the numerator and denominator by the common factors until they have no common factor except 1. The fraction thus obtained is in its simplest form.
The above-given equation: 3 1/4 x 3/5
3 1/4 is a mixed fraction. So convert it into an improper fraction.
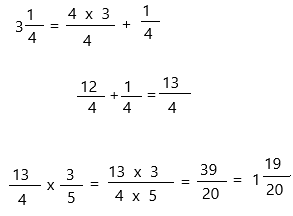
Therefore, 3\(\frac{1}{4}\) × \(\frac{3}{5}\) = 1 19/20
Question 16.
1\(\frac{1}{8}\) × 3\(\frac{2}{3}\)
______________
Answer:
Simplifying a fraction means reducing a fraction to its simplest form. A fraction is in its simplest form if its numerator and denominator have no common factors other than 1.
To simplify fractions, write the factors of the numerator and denominator and mark the common factors in them. Then, divide the numerator and denominator by the common factors until they have no common factor except 1. The fraction thus obtained is in its simplest form.
The above-given equation: 1 1/8 x 3 2/3
both the fractions are mixed fractions. Convert them into improper fractions.
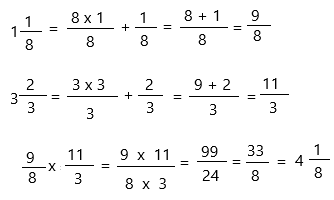
Find each quotient. Use a model. Check using multiplication.
Question 17.
2 ÷ \(\frac{1}{6}\) = ______________
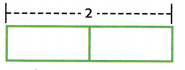
Check ____ × \(\frac{1}{6}\) = ____ or 2
Answer:
The above-given equation:
2 ÷ 1/6
This can be simplified as:
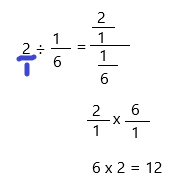
The model can be represented as:
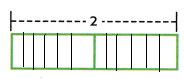
We need to check the answer:
12 x 1/6 = 2
Therefore, the answer is proved.
Question 18.
\(\frac{1}{3}\) ÷ 5 = ______________
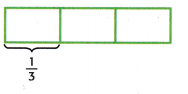
Check ____ × 5 = ____ or \(\frac{1}{3}\)
Answer:
The above-given equation:
1/3 ÷ 5
This can be simplified as:
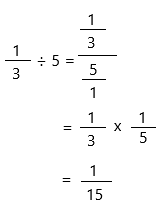
we need to check the answer:
1/15 x 5 = 5/15 = 1/3
Therefore, the answer is proved.
Problem Solving
Question 19.
Ken is working on a project for social studies. He has a piece of poster board that needs to be divided equally into \(\frac{1}{3}\)-foot sections. The poster board is 4 feet wide. How many sections will Ken have
on the poster board?
Answer:
The above-given:
The number of sections that need to be divided equally each = 1/3 foot
The length of feet = 4
The number of sections Ken has on the poster board = B
B = 4 ÷ 1/3
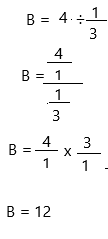
Therefore, he has 12 sections.
Question 20.
Samantha measured the dimensions of a rectangular poster frame. It was \(\frac{3}{4}\)– yard long and \(\frac{1}{2}\)– yard wide. What is the area of the frame?
Answer:
The length of a rectangular poster frame = 3/4
The width of a rectangular poster frame = 1/2
The area of the frame = A
The area of the rectangle = length x width
A = 3/4 x 1/2
A = 3 x 1/ 4 x 2
A = 3/8 square yards.
Therefore, the area of the frame is 3/8 square yards.
Question 21.
At Middle Avenue School, \(\frac{1}{30}\)– of the students are on the track team. The track coach offered to buy pizza or subs for everyone on the team. Of the students for whom the coach bought food, \(\frac{3}{5}\) ordered pizza. What fraction of the students at Middle Avenue School ate pizza?
Answer:
The above-given:
The number of students on the track team = 1/30
The number of students who ordered pizza = 3/5
The fraction of students who ate pizza = F
F = 3/5 of 1/30 students
F = 3/5 x 1/30
F = 3/150
F = 1/50
Therefore, 1/50 is the required fraction of who ate pizza.
Question 22.
Saraid is dividing \(\frac{1}{4}\)– pound of cashews into 5 plastic bags. What fraction of a pound of cashews will be in each plastic bag? Draw a model to help you solve.
Answer:
The above-given:
The number of pounds of cashews Saraid is dividing = 1/4
The number of plastic bags = 5
The fraction of a pound of cashews in each plastic bag = C
C = 1/4 ÷ 5
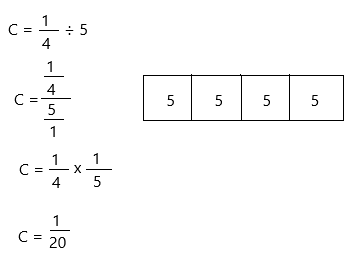
Therefore, each plastic bag have 1/20 pound cashews.
Test Practice
Question 23.
The Great Rope Company sells a rope that is 5 feet long. Juan wants to make sections that are \(\frac{1}{3}\) foot long. How many sections will Juan be able to make? Use the model.
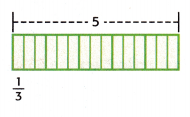
A. 18 sections
B. 15 sections
C. 6 sections
D. 3 sections
Answer: Option B is correct.
The above-given:
The length of rope = 5
The number of sections Juan wants to make each = 1/3
The number of sections he can make = J
J = 5 ÷ 1/3
J = 5/1/1/3
J = 5/1 x 3/1
J = 5 x 3
J = 15
Therefore, he can make 15 sections.
Reflect
Use what you learned about fraction operations to complete the graphic organizer.
Now reflect on the ESSENTIAL QUESTION. Write your answer below.
Answer:

Here are some applications of fractions in real life:
– Dividing pizza slices equally amongst everyone requires fractions.
– In time, Half n hour(1/2) is a common way of expressing 30 minutes.
– To make drinks like mocktails, different fractions of liquids are mixed in the right amounts to get the best outcome.
– If we go to a restaurant with friends and the waitress brings a single bill. To divide the total among the friends, we use fractions.
For example, 11 friends went to a restaurant and the total bill was 3300rs. Now the amount for each friend has to pay?
Now we have to divide the total bill/no. of friends.
3300/11 = 300
Each friend has to pay 300rs.