All the solutions provided in McGraw Hill My Math Grade 4 Answer Key PDF Chapter 14 Lesson 3 Model Angles will give you a clear idea of the concepts.
McGraw-Hill My Math Grade 4 Answer Key Chapter 14 Lesson 3 Model Angles
An angle is a geometric shape that is formed when two rays have the same endpoint.
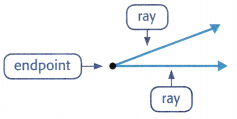
Angles are measured by the amount of rotation, or turning, from one ray to another.
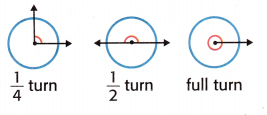
Draw It
Trace the lines to draw an angle that measures \(\frac{1}{4}\) turn. Then draw an angle that measures less than \(\frac{1}{4}\) turn.
1. Draw an angle that measure \(\frac{1}{4}\) turn.
Trace the lines to draw two rays with a common endpoint. The two rays form an angle.
The center of the circle is at the same point as the endpoint of the two rays. The angle you drew measures \(\frac{1}{4}\) turn.

2. Draw an angle that measures less than \(\frac{1}{4}\) turn.
Using the center of the circle as an endpoint, draw a ray that is inside the angle you drew in Step 1.
The ray you drew and the horizontal ray form an angle. This angle measures less than \(\frac{1}{4}\) turn.
Answer:
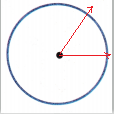
The above figure represents an angle which is less than \(\frac{1}{4}\) turn. The center of the circle is treated as an endpoint of two rays, which forms an angle. At first draw an horizontal ray from the center of the circle. Then, draw a ray as shown in the above figure to form an angle less than \(\frac{1}{4}\) turn.
Try It
Trace the lines to draw an angle that measures \(\frac{1}{4}\) turn. Then draw an angle that measures greater than \(\frac{1}{4}\) turn.
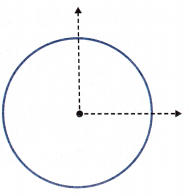
1. Draw an angle that measures \(\frac{1}{4}\) turn.
Trace the lines to draw two rays with a common endpoint. The two rays form an angle.
The center of the circle is at the same point as the endpoint of the two rays.
The angle you drew measures \(\frac{1}{4}\) turn.
2. Draw an angle that measures greater than \(\frac{1}{4}\) turn.
Using the center of the circle as an endpoint, draw a ray that is outside the angle you drew in Step 1.
The ray you drew and the horizontal ray form an angle.
This angle measures greater than \(\frac{1}{4}\) turn.
Answer:
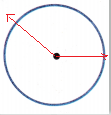
The above figure represents an angle which is greater than \(\frac{1}{4}\) turn. The center of the circle is treated as an endpoint of two rays, which forms an angle. At first draw an horizontal ray from the center of the circle. Then, draw a ray as shown in the above figure to form an angle greater than \(\frac{1}{4}\) turn.
Talk About It
Question 1.
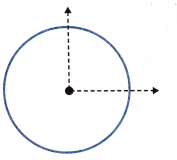
Mathematical PRACTICE Draw a Conclusion Without drawing a circle, determine whether the angle at the right has a measure that is greater than, less than, or equal to \(\frac{1}{2}\) turn. Explain.
![]()
Answer: Equal to \(\frac{1}{2}\) turn
The angle measured here is equal to \(\frac{1}{2}\) turn. Take a point as reference. Take a thread at that reference point and trace the horizontal line and rotate the tread in half turn, which then forms the required angle.
Question 2.
Mathematical PRACTICE Explain to a Friend Refer to the angle you drew in the activity above. State whether the angle’s measure is greater than, less than, or equal to \(\frac{1}{2}\) turn. Explain.
Answer: Equal to \(\frac{1}{2}\) turn
The angle measured here is equal to \(\frac{1}{2}\) turn. Take a point as reference. Take a thread at that reference point and trace the horizontal line and rotate the tread in half turn, which then forms the required angle.
Practice it
Question 3.
Draw an angle with a measure less than \(\frac{1}{4}\) turn.
Answer:
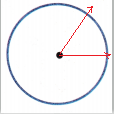
The above figure represents an angle which is less than \(\frac{1}{4}\) turn. The center of the circle is treated as an endpoint of two rays, which forms an angle. At first draw an horizontal ray from the center of the circle. Then, draw a ray as shown in the above figure to form an angle less than \(\frac{1}{4}\) turn.
Question 4.
Draw an angle with a measure greater than \(\frac{1}{4}\) turn.

Answer:
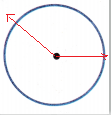
The above figure represents an angle which is greater than \(\frac{1}{4}\) turn. The center of the circle is treated as an endpoint of two rays, which forms an angle. At first draw an horizontal ray from the center of the circle. Then, draw a ray as shown in the above figure to form an angle greater than \(\frac{1}{4}\) turn.
Draw lines to match each figure to its description.
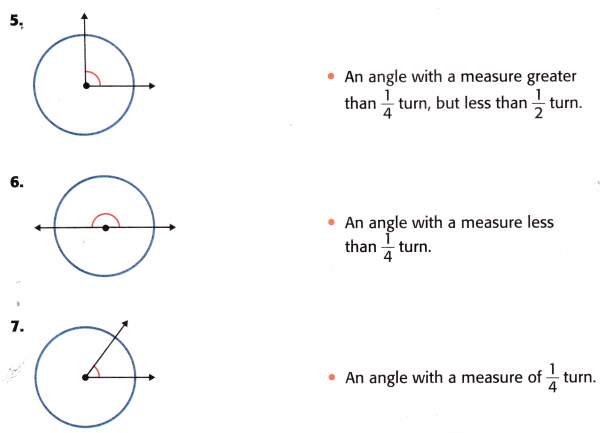

Answer:
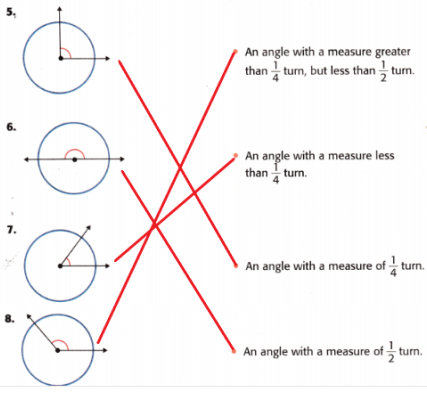
5. An angle with a measure of \(\frac{1}{4}\) turn.
6. An angle with a measure of \(\frac{1}{2}\) turn.
7. An angle with a measure less than \(\frac{1}{4}\) turn.
8. An angle with a measure greater than \(\frac{1}{4}\) turn, but less than \(\frac{1}{2}\) turn.
Apply It
Question 9.
Draw the hands on the clock below to show 5:00.

Describe the measure of the angle formed by the hands of the clock.
Answer:

Clock can be represented as a circle with 360 degrees in it, and that each number indicates an angle with a separation of 360/12 = 30. So, the angle between each number can be consider as 30 degrees.
To illustrate the angle between the hands of a clock at 5:00, the hour hand is on two at 5:00 and the minute hand is on twelve. Therefore, 5 * 30 = 150. The angle at 5:00 is 150 degrees.
Question 10.
Draw a real-world object that shows an angle with a measure of \(\frac{1}{4}\) turn.
Answer: \(\frac{1}{4}\) turn can be considered as 90 degrees as \(\frac{1}{4}\) th part of 360 degrees is 90 degrees.
The real world example for a 90 degrees angle is that a clock that shows 3:00, as the hour hand is on two at 3:00 and the minute hand is on twelve. It can be given as 3 * 30 = 90. The angle at 3:00 is 90 degrees. It can be illustrated as the figure given below.
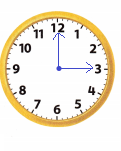
Other real world examples with \(\frac{1}{4}\) turn or 90 degrees are geometrical shapes rectangle and square that have a measurement of all four angles as 90 degrees.
Question 11.
Mathematical PRACTICE Model Math Draw two angles that share a common endpoint and a common ray. Together, they should form an angle with a measure of \(\frac{1}{4}\) turn.
Answer: When two angles are having common endpoint and a common ray, then they are said to be Adjacent angles. The endpoint of the rays, forming the sides of an angle, is called the vertex of an angle.
\(\frac{1}{4}\) turn can be considered as 90 degrees as \(\frac{1}{4}\) th part of 360 degrees is 90 degrees. An adjacent angle is complementary to another if the total of its adjacent angles is 90 degrees.
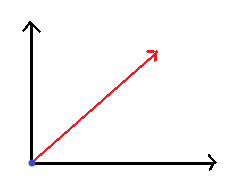
The above figure represents the adjacent angles. As you can observe, there is a common endpoint and common ray which is forming an angle with a measure of \(\frac{1}{4}\) turn.
Write About It
Question 12.
How can I describe an angle’s measure?
Answer: An angle is a geometric shape that is formed when two rays have the same endpoint. The rotation of a ray’s beginning point to its endpoint is referred to as an angle. The amount of rotation from a ray’s initial point to its endpoint is measured as an angle. If the rotation is in the clockwise direction, the angle is said to be positive; if in the anticlockwise direction, it is said to be negative.
Angles are measured by the amount of rotation, or turning, from one ray to another. Angles are typically expressed in terms of degrees. A complete rotation in either a clockwise or counterclockwise direction, with the beginning and ending points being the same, is referred to as a degree. There are 360 parts in a rotation. It is said to be 1 degree if the rotation from the initial and ending side is \(\frac{1}{360}\)th of the rotation.
McGraw Hill My Math Grade 4 Chapter 14 Lesson 3 My Homework Answer Key
Practice
Circle the correct description for the measure of each angle.
Question 1.
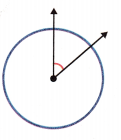
less than \(\frac{1}{4}\) turn
greater than \(\frac{1}{4}\) turn
Answer: less than \(\frac{1}{4}\) turn
The above figure represents an angle which is less than \(\frac{1}{4}\) turn. The center of the circle is treated as an endpoint of two rays, which forms an angle. \(\frac{1}{4}\) turn can be considered as 90 degrees as \(\frac{1}{4}\) th part of 360 degrees is 90 degrees. So, in the above given figure, the angle is less than 90 degrees.
Question 2.
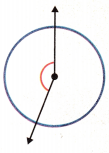
less than \(\frac{1}{4}\) turn
greater than \(\frac{1}{4}\) turn
Answer: greater than \(\frac{1}{4}\) turn
The above figure represents an angle which is greater than \(\frac{1}{4}\) turn. The center of the circle is treated as an endpoint of two rays, which forms an angle. \(\frac{1}{4}\) turn can be considered as 90 degrees as \(\frac{1}{4}\) th part of 360 degrees is 90 degrees. So, in the above given figure, the angle is greater than 90 degrees.
Question 3.
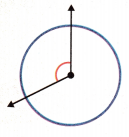
less than \(\frac{1}{2}\) turn
greater than \(\frac{1}{3}\) turn
Answer: less than \(\frac{1}{2}\) turn
The above figure represents an angle which is less than \(\frac{1}{2}\) turn. The center of the circle is treated as an endpoint of two rays, which forms an angle. \(\frac{1}{2}\) turn can be considered as 180 degrees as \(\frac{1}{2}\)th part of 360 degrees is 180 degrees. So, in the above given figure, the angle is less than 180 degrees.
Draw an angle with a measure greater than turn.
Question 4.
\(\frac{1}{4}\) turn

Answer:
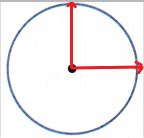
The above figure represents an angle with \(\frac{1}{4}\) turn. The center of the circle is treated as an endpoint of two rays, which forms an angle. At first draw an horizontal ray from the center of the circle. Then, draw a ray as shown in the above figure to form an angle with \(\frac{1}{4}\) turn.
Question 5.
\(\frac{1}{2}\) turn

Answer:
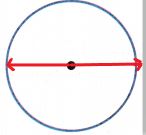
The above figure represents an angle with \(\frac{1}{2}\) turn. The center of the circle is treated as an endpoint of two rays, which forms an angle. At first draw an horizontal ray from the center of the circle. Then, draw a ray as shown in the above figure to form an angle with \(\frac{1}{2}\) turn.
Question 6.
greater than \(\frac{1}{2}\) turn

Answer:
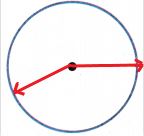
The above figure represents an angle which is greater than \(\frac{1}{2}\) turn. The center of the circle is treated as an endpoint of two rays, which forms an angle. At first draw an horizontal ray from the center of the circle. Then, draw a ray as shown in the above figure to form an angle greater than \(\frac{1}{2}\) turn.
Question 7.
less than \(\frac{1}{4}\) turn

Answer:
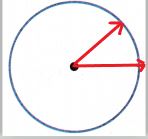
The above figure represents an angle which is less than \(\frac{1}{4}\) turn. The center of the circle is treated as an endpoint of two rays, which forms an angle. At first draw an horizontal ray from the center of the circle. Then, draw a ray as shown in the above figure to form an angle less than \(\frac{1}{4}\) turn.
Problem Solving
Question 8.
Mathematical PRACTICE Be Precise Describe the rays of an angle that measures \(\frac{1}{2}\) turn.
Answer: A \(\frac{1}{2}\) turn is termed as a straight angle which has a measure of 180 degrees. It is termed as such because it looks like a straight line. A ray is part of a line.
Question 9.
Mathematical PRACTICE Model Math Imagine a clock with the hour hand at 12 and the minute hand at 2. Does the angle formed by the two hands have a measure greater than, less than, or equal to \(\frac{1}{4}\) turn?
Answer: less than \(\frac{1}{4}\) turn
Consider the fact that a clock has 360 degrees and is shaped like a circle. 60 minutes make to an hour, thus 360 degrees divided by that number equals 6. The minute hand therefore rotates six degrees per minute. The hour hand rotates around the clock in 720 minutes. 720 minutes divided by 360 degrees equals 0.5. The hour hand therefore moves 0.5 degrees per minute.
At 12:10, the hour hand has moved 10 out of 720 possible times from the top of the clock. 10 times 0.5 degrees is 5 degrees. At 12:10, the minute hand has moved 10 out of 60 possible times from the top of the clock. 10 times 6 degrees is 60 degrees. Therefore, 60 – 5 = 55 degrees.
\(\frac{1}{4}\) turn can be considered as 90 degrees as \(\frac{1}{4}\) th part of 360 degrees is 90 degrees. As 55 degrees is less than 90 degrees, the angle formed by a clock with the hour hand at 12 and the minute hand at 2 is less than \(\frac{1}{4}\) turn.
Vocabulary Check
Question 10.
In your own words, define angle.
Answer: An angle is a geometric shape that is formed when two rays have the same endpoint. The rotation of a ray’s beginning point to its endpoint is referred to as an angle. The amount of rotation from a ray’s initial point to its endpoint is measured as an angle. If the rotation is in the clockwise direction, the angle is said to be positive; if in the anticlockwise direction, it is said to be negative.
Angles are measured by the amount of rotation, or turning, from one ray to another. Angles are typically expressed in terms of degrees. A complete rotation in either a clockwise or counterclockwise direction, with the beginning and ending points being the same, is referred to as a degree. There are 360 parts in a rotation. It is said to be 1 degree if the rotation from the initial and ending side is \(\frac{1}{360}\)th of the rotation.