All the solutions provided in McGraw Hill My Math Grade 4 Answer Key PDF Chapter 14 Lesson 2 Draw Parallel and Perpendicular Lines will give you a clear idea of the concepts.
McGraw-Hill My Math Grade 4 Answer Key Chapter 14 Lesson 2 Draw Parallel and Perpendicular Lines
You can describe lines, rays, and line segments by the way they cross each other or do not cross each other.
Math in My World
Example 1
Oliver was riding in the car and saw this sign. Describe how the outlined line segments cross each other or do not cross each other.

Parallel lines are always the same distance apart. They do not meet or cross each other.
So, Oliver saw a figure with ________________ line segments.
Answer: So, Oliver saw a figure with 4 line segments.
The outlined line segments do not cross each other as they are parallel lines. In the above sign, the opposite line segments are parallel to each other.
The pairs of line segments that do not intersect or meet at any point are called parallel line segments. The lines are in a plane such that they are always the same distance apart and never meet, no matter how far they are extended.
Example 2
Describe the figure. Use parallel, perpendicular, or intersecting. Use the most specific term.
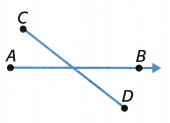
The figure shows ray AB and line segment CD.
The figures cross each other but do not form square corners.
\(\overrightarrow{A B}\) and \(\overline{C D}\) are ________________.
Answer: Intersecting
\(\overrightarrow{A B}\) and \(\overline{C D}\) are Intersecting.
When two or more lines cross each other in a plane, they are called intersecting lines. The intersecting lines share a common point, which exists on all the intersecting lines, and is called the point of intersection.
Talk Math
Name a real-world example of parallel line segments and intersecting line segments.

Answer: Parallel line segment examples in real life are railroad tracks, marking on the streets, zebra crossing on the roads, staircase and railings, etc.
When two or more lines cross each other in a plane, they are called intersecting lines. The intersecting lines share a common point, which exists on all the intersecting lines, and is called the point of intersection. Intersecting line segments examples are Cross roads (two roads meeting at a common point), scissors (the two arms of the scissors), the letter X of English alphabet, etc.
Guided Practice
Question 1.
Describe the line segments outlined on the tennis racquet.

Answer: Parallel line segments
The pairs of line segments that do not intersect or meet at any point are called parallel line segments. The lines are in a plane such that they are always the same distance apart and never meet, no matter how far they are extended.
McGraw Hill My Math Grade 4 Chapter 14 Lesson 2 My Homework Answer Key
Practice
Question 1.
Describe the figure. Use parallel, perpendicular, or intersecting. Use the most specific term.
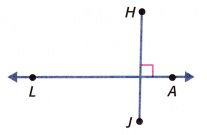
Answer: Perpendicular
A straight line that forms a right angle (90 degrees) with another line is referred to as perpendicular lines. In other words, two lines are said to be perpendicular to one another if they intersect at a right angle.
Here, AL is a line and HJ is a line segment. Both of them intersect each other at right angle (90 degrees) as shown in the figure.
Mathematical PRACTICE Use Symbols Draw an example of each figure.
Question 2.
\(\overleftrightarrow{G P}\) || \(\overleftrightarrow{N D}\)
Answer:
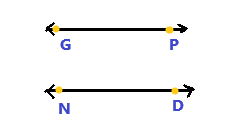
The above figure represents \(\overleftrightarrow{G P}\) || \(\overleftrightarrow{N D}\). GP and ND are both lines in which both are parallel to each other.
The pairs of line segments that do not intersect or meet at any point are called parallel line segments. The lines are in a plane such that they are always the same distance apart and never meet, no matter how far they are extended.
Question 3.
\(\overrightarrow{H Y}\) intersects \(\overline{Q A}\)
Answer:
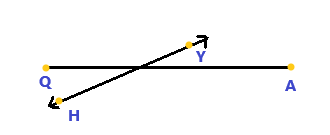
The above figure represents \(\overrightarrow{H Y}\) intersects \(\overline{Q A}\). HY is a line which extends infinitely and QA is a line segment with two endpoints.
When two or more lines cross each other in a plane, they are called intersecting lines. The intersecting lines share a common point, which exists on all the intersecting lines, and is called the point of intersection.
Problem Solving
Question 4.
Mathematical PRACTICE Model Math Martin is washing windows. First he must raise the blinds. Describe the kind of line segments formed by the horizontal blinds.

Answer: Parallel lines
The horizontal blinds of a window are parallel to each other. The pairs of line segments that do not intersect or meet at any point are called parallel line segments. The lines are in a plane such that they are always the same distance apart and never meet, no matter how far they are extended.
Vocabulary Check
Draw a line to match each vocabulary term to its example.
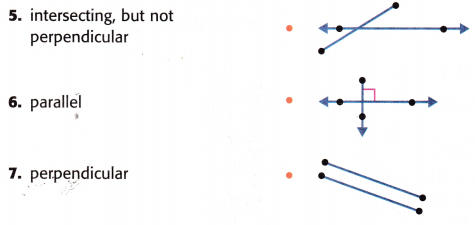
5. intersecting, but not perpendicular- When two or more lines cross each other in a plane, they are called intersecting lines. The intersecting lines share a common point, which exists on all the intersecting lines, and is called the point of intersection.
6. Parallel – The pairs of line segments that do not intersect or meet at any point are called parallel line segments. The lines are in a plane such that they are always the same distance apart and never meet, no matter how far they are extended.
7. Perpendicular – A straight line that forms a right angle (90 degrees) with another line is referred to as perpendicular lines. In other words, two lines are said to be perpendicular to one another if they intersect at a right angle.
Test Practice
Question 8.
Which is the correct description of the figure?
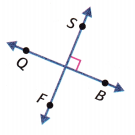
(A) \(\overleftrightarrow{Q B}\) || \(\overleftrightarrow{S F}\)
(B) \(\overleftrightarrow{Q B}\) ⊥ \(\overleftrightarrow{Q B}\)
(C) \(\overleftrightarrow{Q S}\) ⊥ \(\overleftrightarrow{B F}\)
(D) \(\overleftrightarrow{Q S}\) || \(\overleftrightarrow{B F}\)
Answer: \(\overleftrightarrow{Q B}\) ⊥ \(\overleftrightarrow{S F}\)
QB and SF are both line segments, where both intersect each other perpendicularly. A straight line that forms a right angle (90 degrees) with another line is referred to as perpendicular lines. In other words, two lines are said to be perpendicular to one another if they intersect at a right angle.