All the solutions provided in McGraw Hill My Math Grade 4 Answer Key PDF Chapter 13 Lesson 5 Relate Area and Perimeter will give you a clear idea of the concepts.
McGraw-Hill My Math Grade 4 Answer Key Chapter 13 Lesson 5 Relate Area and Perimeter
Math in My World
Example 1
The swim team put its trophy on a table that has an area of 12 square feet. List all of the possible lengths and widths of rectangles with an area of 12 square feet.

The models show all of the possible rectangles. Label each model.
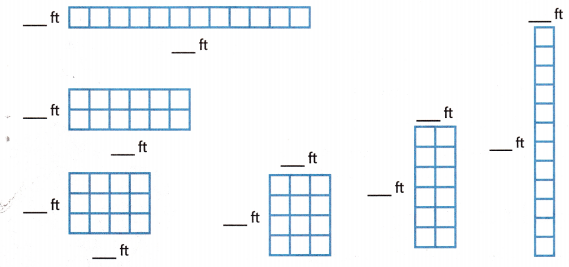
So, the table could have the following possible lengths and widths.
_____________ × _______________ = 12
_____________ × _______________ = 12
_____________ × _______________ = 12
_____________ × _______________ = 12
_____________ × _______________ = 12
_____________ × _______________ = 12
Answer: Given the figures,
We will find the possible lengths and widths.
The possible lengths and widths are,
12 ft x 1 ft = 12 ft
2 ft x 6 ft = 12 ft
3 ft x 4 ft = 12 ft
4 ft x 3 ft = 12 ft
6 ft x 2 ft = 12 ft
12 ft x 1 ft = 12 ft
Example 2
Find the rectangle with the greatest area whose perimeter is 14 units.
The table shows each rectangle that has a perimeter of 14 units. Complete the table.
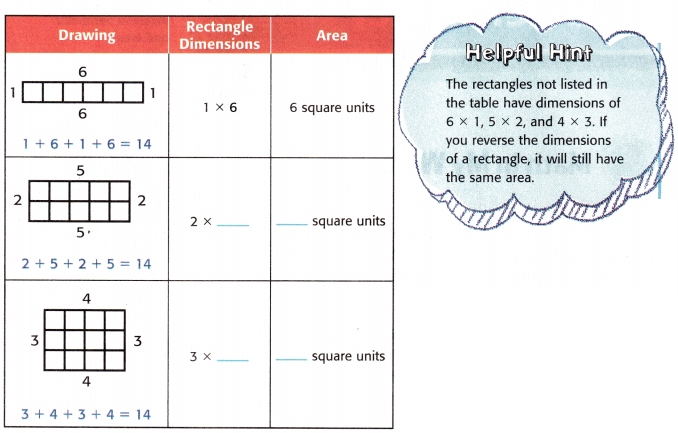
The greatest area is ____________ square units.
So, the rectangle with the greatest area is ____________ units by ____________ units. Its area is ____________ square units.
Answer: Given the figure, we will find the width and area of the rectangle figures.
(i) The given figure, consists of a length is 2 units and width is 5 units.
The formula for the area of a rectangle is l x w
A = 2 x 5 = 10 square units.
(ii) Given that, the figure consists of 3 units and 4 units.
Now, find the area of a rectangle.
The formula for the area of the rectangle is, l x w
A = 3 x 4 = 12 square units.
Now, find the greatest area of a rectangle.
The greatest area of a rectangle is 12 square units.
So, the rectangle with the greatest area is 3 units by 4 units. Its area is 12 square units.
Talk Math
Which rectangle in Example 2 has the least area?

Answer: The least area in Example 2 is 6 square units.
Guided Practice
List all the possible dimensions of rectangles for each area.
Question 1.
9 square units
_____________ × _______________
_____________ × _______________
_____________ × _______________
Answer: Given the area of a rectangle is 9 square units.
Now, write the possible dimensions of the rectangle area.
The formula for the area of a rectangle is l x w. So, the possible dimensions are
1 x 9 = 9
3 x 3 = 9
9 x 1 = 9
Question 2.
14 square units
_______________
_______________
_______________
_______________
Answer: Given the area of the rectangle is 14 square units.
We will write the possible dimensions of the rectangle area.
The area of a rectangle formula is l x w. So, the possible dimensions are,
1 x 14 = 14
2 x 7 = 14
7 x 2 = 14
14 x 1 = 14
Independent Practice
List all the possible dimensions of rectangles for each area.
Question 3.
16 square units
Answer: Given that the area of a rectangle is 16 sq. units.
We will write the possible dimensions of the area of a rectangle.
The area of a rectangle is l x w.
So, the possible dimensions are,
1 x 16 = 16
2 x 8 = 16
4 x 4 = 16
8 x 2 = 16
16 x 1 = 16
Question 4.
20 square units
Answer: Given that the area of a rectangle is 20 sq. units.
We will write the possible dimensions of the area of a rectangle.
The area of a rectangle is l x w.
So, the possible dimensions are
1 x 20 = 20
2 x 10 = 20
4 x 5 = 20
5 x 4 = 20
Find the perimeter and area for each square or rectangle.
Question 5.

Perimeter: ________________
Area: ________________
Answer: The perimeter of a square is, 4s = 4 x 4 = 16 units.
The area of a square is, s x s = 4 x 4 = 16.
Explanation: Given the figure, it consists of a length and width is 4 units.
So, the figure is square in shape.
Now, we will find the area of a square and the perimeter of a square.
The perimeter of a square formula is, 4 x s = 4 x 4 = 16 units.
The formula for the area of the square is, S x S.
A = 4 x 4 = 16 sq.units.
Question 6.

Perimeter: ________________
Area: ________________
Answer: The perimeter of a rectangle is 20 units.
The area of a rectangle is, l x w = 8 x 2 = 16 sq.units.
Explanation: The given figure consists of a length is 8 units and width is 2 units.
Now, we will find the area and perimeter of a rectangle.
The formula for the perimeter of a rectangle is 2(l+w).
The perimeter of a rectangle is, 2(8+2) = 2(10) = 20 units.
The area of a rectangle formula is l x w.
So, the area of a rectangle is 8 x 2 = 16 sq.units
Question 7.
What do the figures in Exercises 5 and 6 have in common? How do these figures differ?
Answer: The exercise 5 and 6 figures both have the same area. But they have different perimeters.
Problem Solving
Question 8.
Mathematical PRACTICE Plan Your Solution Violet is making a rectangular banner for the basketball team to run through before the start of the game. She has 24 square feet of paper. List all of the possible dimensions of rectangles with an area of 24 square feet.

Answer: Given the area is 24 sq. ft.
We will write the possible dimensions of rectangles with an area of 24 sq. ft.
The possible dimensions are,
2 ft x 12 ft = 24 sq. feet
3 ft x 8 ft = 24 sq. ft
4 ft x 6 ft = 24 sq. ft
6 ft x 4 ft = 24 sq.ft
8 ft x 3 ft = 24 sq. ft
12 ft x 2 ft = 24 sq.ft
24 ft x 1 ft = 24 sq. ft
Question 9.
Which of the dimensions found in Exercise 8 has the greatest perimeter?
Answer: The greatest perimeter dimensions found in exercise 8 is 1ft x 24 ft or 24 ft x 1 ft.
Question 10.
If a rectangle has a greater perimeter than another rectangle, does it also have a greater area? Explain.
Answer: No. There is no such particular relation between perimeter and area, sometimes perimeter>area but sometimes area>perimeter. It mainly depends on the values.
HOT Problems
Question 11.
Mathematical PRACTICE Reason Is it possible to draw a rectangle that has an area of 24 square units and a perimeter of 24 units? Explain.
Answer: It is not possible to draw a rectangle that will have an area of 24 square units and a perimeter of 24 units.
Explanation: The formula for the area of a rectangle is l x w.
The given area of a rectangle is 24 square units.
The factors of 24 are 1, 2, 3, 4, 6, 8, 12, and 24.
Using each pair of factors, we will find the perimeter of 24 units.
The perimeter of a rectangle is 2(l+w)
1 and 24, the perimeter is 50.
2 and 12, the perimeter is 28.
3 and 8, the perimeter is 22.
4 and 6 perimeter is 20.
So, it’s not possible to draw a rectangle with an area and perimeter are 24.
Question 12.
Building on the Essential Question What is the difference between area and perimeter?
Answer: The perimeter is used to measure the distance of the outer surface of the shape, whereas the area is used to measure the inner surface of the shape.
McGraw Hill My Math Grade 4 Chapter 13 Lesson 5 My Homework Answer Key
Practice
Draw two possible rectangles for each perimeter. Find the area of each.
Question 1.
20 units
Answer: Given the perimeter of a rectangle is 20 units, draw the possible rectangles.
The two possible rectangles are,
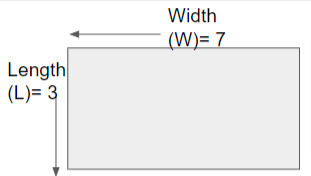
The area of a rectangle formula is, l x w
A = 7 x 3 = 21 square units.
Another possible way of the rectangle is,
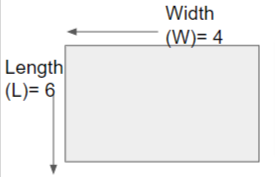
The area of a rectangle formula is l x w.
A = 6 x 4 = 24 square units.
Question 2.
8 units
Answer: Given the perimeter of a rectangle is 8 units, draw the possible rectangles.
The possible way of the rectangle is,

The formula for the area of a rectangle is, l x w
A = 1 x 3 = 3 sq.units.
Another way of the possible rectangle is,
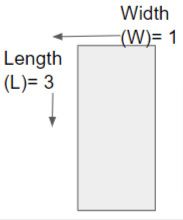
The area of a rectangle formula is, l x w
A = 3 x 1 = 3 sq.units.
Problem Solving
Question 3.
Mathematical PRACTICE Use Number Sense Tomas drew a rectangle with an area of 6 square centimeters. What is the greatest possible perimeter for this rectangle?
Answer: The greatest possible perimeter of a rectangle is 14.
Explanation: The area of a rectangle formula is l x w.
The given area of a rectangle is 6 sq. cm. It means multiplying the length and width would give us 6.
6 will obtain by, 1 x 6=6 and 2 x 3=6
Let’s find the perimeter, by using 1 and 6.
The formula for the Perimeter of a rectangle is 2(l+w)
P =2(1+6) = 2(7)
P = 14
Now, find the perimeter by using 2 and 3.
P = 2(2+3) = 2(5)
P = 10.
So, the greatest possible perimeter of the rectangle is 14.
Question 4.
Danica has laid out floor tiles so they form a rectangle with a perimeter of 18 inches. What is the difference between the greatest and least possible areas of the rectangle?
Answer: The difference between the greatest and possible areas of the rectangle is 20-8 = 12 inches.
Explanation: Given that, the perimeter of a rectangle is 18 inches.
P= 2(l+w)
2(l+w)= 18
l+w = 18/2 =9.
Now, find the possible pairs of integers, the sum of integers is 9.
The possible pairs are, (8,1), (7,2), (6,3), (5,4)
Now, find the area of each pair.
The area of the rectangle formula is, l x w
A = 8 x 1 = 8
A = 7 x 2 = 14
A = 6 x 3 = 18
A = 5 x 4 = 20
So, the greatest and least area of the rectangle is 20 and 8.
The difference is 20 – 8 = 12 inches.
Question 5.
A rectangle has an area of 30 square meters and a perimeter of 34 meters. What are the dimensions of the rectangle?
Answer: The dimensions of the rectangle are, 15 and 2.
Explanation: Given that, the area of a rectangle is 30 sq.m
Now, find the dimensions of the rectangle.
The area of a rectangle formula is l x w.
A = 15 x 2 = 30 sq.m
We get the given area value.
The perimeter of a rectangle is 2(l+w)
P = 2(15+2) = 2(17) = 34 meters.
we get the given perimeter value.
So, the dimensions of the rectangle are 15 and 7.
Test Practice
Question 6.
A square has a perimeter of 28 feet. What is its area?
(A) 45 square feet
(B) 48 square feet
(C) 49 square feet
(D) 50 square feet
Answer: C
Explanation: Given that, the perimeter of a square is 28 ft.
The formula for the perimeter of a square is 4S.
So, we get the perimeter value as 4 x 7 = 28 ft.
Now, find the area of a square.
The area of a square formula is S x S.
Based on the perimeter of a square value, one side of a square is 7ft.
A = 7 x 7 = 49 sq.ft
So, option C is correct.