All the solutions provided in McGraw Hill My Math Grade 4 Answer Key PDF Chapter 13 Lesson 4 Measure Area will give you a clear idea of the concepts.
McGraw-Hill My Math Grade 4 Answer Key Chapter 13 Lesson 4 Measure Area
You know that area is the number of square units needed to cover a region or figure without any overlap.
Math in My World
Example 1
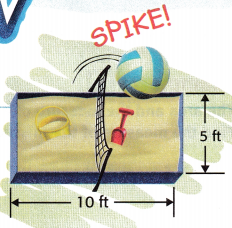
The Perez family wants to put the sandbox shown in their backyard. What is the area of the sandbox?
One Way:
Count unit squares.
Tile the rectangle with unit squares. Each unit square has an area of one square foot.
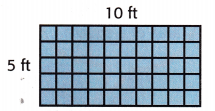
There are ______________ unit squares.
There are ______________ square feet.
Another Way:
Multiply.
Multiply the length times the width to find the area.
A = length × width
A = l × w
A = 10 feet × 5 feet
A = ___________ square feet
So, the area of the sandbox is _____________ square feet.
Answer: Given that, the rectangular sandbox.
The length of the box is 10 ft and the width is 5 ft.
We are using two ways, to find the area.
One way,
Count the length and width of unit squares and multiply them.
So, there are 5 x 10 unit squares.
There are 50 square feet.
Another way:
Using the formula way,
The area of a rectangle formula is l x w
Area = 10 ft x 5 ft
A = 50 square feet
So, the area of the rectangular sandbox is 50 square feet.
Example 2
The area and the measure of one side of the square are given. Find the measure of the missing side.
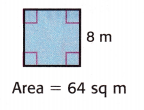
A = s × s Write the formula.
64 = 8 × s
Think: 8 times what number equals 64?
s = _____________ meters
The measure of the missing side is _____________ meters.
Answer: S = 8 meters.
Explanation: Given the square, the one side of a square is 8m.
The square has equal sides.
Now, find the area of a square.
The formula for the area of a square is s x s.
A = 8 x 8 = 64 sq . m
We get the given area value.
So, the missing measure of the missing side is 8 meters.
Talk Math
Describe two ways to find the area of a square.

Answer:
One Way:
Count unit squares.
Tile the rectangle with unit squares. Each unit square has an area of one square foot.
Another Way:
Multiply.
Multiply the length times the width to find the area.
A = length × width
A = l × w
Guided Practice
Find the area of each square or rectangle.
Question 1.

A = ______________
Answer: A= 8 x 4 = 32 sq.units
Explanation: Given the rectangle figure,
The figure consists of a length is 8 units and width is 4 units.
Now, find the area of a rectangle.
The area of a rectangle formula is, l x w
So, A = 8 x 4 = 32 sq.units
Question 2.
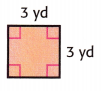
A = ______________
Answer: 9 square yd
Explanation: Given the square figure, with side is 3 yd.
We will find the area of the square.
The area of a square formula is, s x s
So, A = 3 x 3 = 9 square yard.
McGraw Hill My Math Grade 4 Chapter 13 Lesson 4 My Homework Answer Key
Practice
Find the area of each figure.
Question 1.
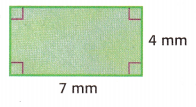
A = _____________ square millimeters
Answer: 28 square millimeters
Explanation: Given the figure,
The figure is rectangular in shape.
The length and width of the rectangle are 7mm and 4 mm.
We need to find the area of a rectangle.
The formula for the area of a rectangle is, l x w
A = 7 x 4 = 28 sq.mm
Question 2.

A = _____________ square units
Answer: A = 4 Square units
Explanation: Given the square figure,
The side of a square is 2 units.
Now, find the area of a square.
The Area of a square formula is, s x s
A = 2 x 2 = 4 sq. units
Question 3.

A = _____________ square units
Answer: A = 15 square units.
Explanation: The given rectangle figure consists of 5 units and 3 units.
We will find the area of a rectangle.
The Area of a rectangle formula is, l x w
A = 5 x 3 = 15 sq.units.
Question 4.
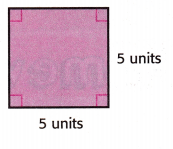
A = _____________ square units
Answer: A = 25 square units
Explanation: Given the square figure, the side of a square is 5 units.
Now, find the area of a square.
The area of a square formula is, s x s
A = 5 x 5 = 25 sq. units.
Problem Solving
Question 5.
Mathematical PRACTICE Justify Conclusions One side of a square is 10 units. Which is greater, the number of square units for the area of the square or the number of units for the perimeter? Explain.
Answer: The area of a square will be greater.
Explanation: Given that one side of a square is 10 units.
We will find the area of a square and the perimeter of a square.
The formula for the area of the square is, s x s
A = 10 x 10 = 100 square units.
Now, find the perimeter of a square.
The perimeter of a square is, 4s = 4 x 10 = 40 units.
Comparing the area and perimeter of a square. The area of a square is greater.
Question 6.
Eric created a rectangular patio using 1-foot square paving stones, which are sold in batches by the dozen. The patio measures 7 feet by 8 feet. How many batches of paving stones did Eric need? (Hint: 1 dozen = 12)
Answer: Eric needs 5 Batches of paving stones.
Explanation: Given that, the patio measures are 7 ft and 8ft.
Eric creates a rectangular patio using 1-foot square paving stones.
Now, we will find how many batches of paving stones are needed.
First, multiply 8 and 7 we get the needed stones.
So, 8 x 7 = 56 stones.
The paving stones are sold in batches by the dozen. (1 dozen = 12)
We need to find how many times 12 goes into 56.
But, the 12 cannot go into 56 evenly, so12 x 5=60 which will be more than enough stones for Eric’s patio.
Therefore, Eric needs 5 batches of paving stones for his patio.
Test Practice
Question 7.
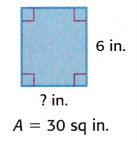
What is the perimeter of the rectangle?
(A) 22 inches
(B) 24 inches
(C) 26 inches
(D) 28 inches
Answer: (A) 22 inches
Explanation: Given the length of the rectangle is 6 in and the area is 30 sq. in.
Now, we will find the perimeter of the rectangle.
The perimeter of a rectangle formula is 2(l+w)
So, we will find the width value.
The area of a rectangle is l x w
A = l x w
30 = 6 x w
30/6 = w
width = 5
The perimeter of a rectangle is, 2(l+w)
P = 2(6+5) = 2(11)
The perimeter of a rectangle is 22 inches.
So, option C is correct.