All the solutions provided in McGraw Hill My Math Grade 4 Answer Key PDF Chapter 10 Lesson 6 Use Place Value and Models to Add will give you a clear idea of the concepts.
McGraw-Hill My Math Grade 4 Answer Key Chapter 10 Lesson 6 Use Place Value and Models to Add
Math in My World
Example 1
Denny walked \(\frac{3}{10}\) mile to the post office. Then he walked \(\frac{5}{100}\) mile to the grocery store. How far did he walk in all? Write the answer as a fraction with a denominator of 100 and as a decimal.

Use a model to show \(\frac{3}{10}\) + \(\frac{5}{100}\).
1. Write \(\frac{3}{10}\) as a fraction with a denominator of 100.
The decimal models show that \(\frac{3}{10}\) = \(\frac{30}{100}\).

2. Add like fractions.
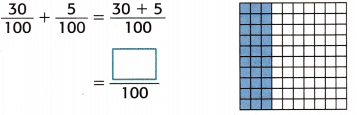
3. Write the sum as a decimal.
Think of \(\frac{35}{100}\) as thirty-five hundredths. So, \(\frac{35}{100}\) = 0.35.
So, \(\frac{3}{10}\) + \(\frac{5}{100}\) = \(\frac{35}{100}\), or _______________.
Denny walked \(\frac{35}{100}\), or 0.35, mile in all.
Answer: In order to make the denominators of both fractions same for addition, multiply and divide \(\frac{3}{10}\) by 10. Then, it becomes \(\frac{30}{100}\)
Now, \(\frac{30}{100}\) + \(\frac{5}{100}\) = \(\frac{35}{100}\)

\(\frac{35}{100}\) = 0.35 in decimal
Example 2
Find \(\frac{4}{10}\) + \(\frac{22}{100}\). Write the sum as a fraction with a denominator of 100 and as a decimal.
1. Write \(\frac{4}{10}\) as a fraction with a denominator of 100.
The decimal models show that \(\frac{4}{10}\) = \(\frac{40}{100}\).

2. Add like fractions.
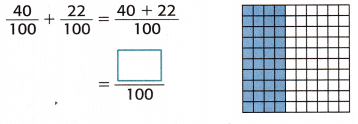
3. Write the sum as a decimal.
Think of \(\frac{62}{100}\) as sixty-two hundredths. So, \(\frac{62}{100}\) = 0.62.
So, \(\frac{4}{10}\) + \(\frac{22}{100}\) = \(\frac{62}{100}\) or _____________.
Check:
The models show that \(\frac{4}{10}\) + \(\frac{22}{100}\) = \(\frac{62}{100}\) or 0.62

Answer: In order to make the denominators of both fractions same for addition, multiply and divide \(\frac{4}{10}\) by 10. Then, it becomes \(\frac{40}{100}\)
Now, \(\frac{40}{100}\) + \(\frac{22}{100}\) = \(\frac{62}{100}\)

\(\frac{62}{100}\) = 0.62 in decimal
Talk Math
In Example 2, why was \(\frac{4}{10}\) written as \(\frac{40}{100}\)?

Answer: For calculating sum of two fractions, we need like fractions. In order to make the denominators of both fractions same for addition, multiply and divide \(\frac{4}{10}\) by 10. Then, it becomes \(\frac{40}{100}\). Now, as the denominators are same, we can simply perform addition of numerators.
Guided Practice
Add. Write each sum as a fraction with a denominator of 100 and as a decimal.
Question 1.
\(\frac{5}{10}\) + \(\frac{1}{100}\) = _______________
Answer: \(\frac{51}{100}\) = 0.51
In order to make the denominators of both fractions same for addition, multiply and divide \(\frac{5}{10}\) by 10. Then, it becomes \(\frac{50}{100}\)
Now, \(\frac{50}{100}\) + \(\frac{1}{100}\) = \(\frac{51}{100}\)
\(\frac{51}{100}\) = 0.51 in decimal
Question 2.
\(\frac{7}{10}\) + \(\frac{13}{100}\) = ________________
Answer: \(\frac{83}{100}\) = 0.83
In order to make the denominators of both fractions same for addition, multiply and divide \(\frac{7}{10}\) by 10. Then, it becomes \(\frac{70}{100}\)
Now, \(\frac{70}{100}\) + \(\frac{13}{100}\) = \(\frac{83}{100}\)
\(\frac{83}{100}\) = 0.83 in decimal
Independent Practice
Shade the models to find each sum. Write the sum as a fraction with a denominator of 100.
Question 3.
\(\frac{2}{10}\) + \(\frac{37}{100}\) = ______________

Answer: \(\frac{57}{100}\) = 0.57

In order to make the denominators of both fractions same for addition, multiply and divide \(\frac{2}{10}\) by 10. Then, it becomes \(\frac{20}{100}\)
Now, \(\frac{20}{100}\) + \(\frac{37}{100}\) = \(\frac{57}{100}\)
\(\frac{57}{100}\) = 0.57 in decimal
Question 4.
\(\frac{7}{10}\) + \(\frac{11}{100}\) = ________________

Answer: \(\frac{81}{100}\) = 0.81

In order to make the denominators of both fractions same for addition, multiply and divide \(\frac{7}{10}\) by 10. Then, it becomes \(\frac{70}{100}\)
Now, \(\frac{70}{100}\) + \(\frac{11}{100}\) = \(\frac{81}{100}\)
\(\frac{81}{100}\) = 0.81 in decimal
Add. Write each sum as a fraction with a denominator of 100 and as a decimal.
Question 5.
\(\frac{6}{10}\) + \(\frac{24}{100}\) = _________________
Answer: \(\frac{84}{100}\) = 0.84
In order to make the denominators of both fractions same for addition, multiply and divide \(\frac{6}{10}\) by 10. Then, it becomes \(\frac{60}{100}\)
Now, \(\frac{60}{100}\) + \(\frac{24}{100}\) = \(\frac{84}{100}\)
\(\frac{84}{100}\) = 0.84 in decimal
Question 6.
\(\frac{5}{10}\) + \(\frac{21}{100}\) = _________________
Answer: \(\frac{71}{100}\) = 0.71
In order to make the denominators of both fractions same for addition, multiply and divide \(\frac{5}{10}\) by 10. Then, it becomes \(\frac{50}{100}\)
Now, \(\frac{50}{100}\) + \(\frac{21}{100}\) = \(\frac{71}{100}\)
\(\frac{71}{100}\) = 0.71 in decimal
Question 7.
\(\frac{3}{10}\) + \(\frac{65}{100}\) = _________________
Answer: \(\frac{95}{100}\) = 0.95
In order to make the denominators of both fractions same for addition, multiply and divide \(\frac{3}{10}\) by 10. Then, it becomes \(\frac{30}{100}\)
Now, \(\frac{30}{100}\) + \(\frac{65}{100}\) = \(\frac{95}{100}\)
\(\frac{95}{100}\) = 0.95 in decimal
Question 8.
\(\frac{1}{10}\) + \(\frac{52}{100}\) = _________________
Answer: \(\frac{62}{100}\) = 0.62
In order to make the denominators of both fractions same for addition, multiply and divide \(\frac{1}{10}\) by 10. Then, it becomes \(\frac{10}{100}\)
Now, \(\frac{10}{100}\) + \(\frac{52}{100}\) = \(\frac{62}{100}\)
\(\frac{62}{100}\) = 0.62 in decimal
Question 9.
\(\frac{8}{10}\) + \(\frac{17}{100}\) = _________________
Answer: \(\frac{97}{100}\) = 0.97
In order to make the denominators of both fractions same for addition, multiply and divide \(\frac{8}{10}\) by 10. Then, it becomes \(\frac{80}{100}\)
Now, \(\frac{80}{100}\) + \(\frac{17}{100}\) = \(\frac{97}{100}\)
\(\frac{97}{100}\) = 0.97 in decimal
Question 10.
\(\frac{2}{10}\) + \(\frac{42}{100}\) = _________________
Answer: \(\frac{62}{100}\) = 0.62
In order to make the denominators of both fractions same for addition, multiply and divide \(\frac{2}{10}\) by 10. Then, it becomes \(\frac{20}{100}\)
Now, \(\frac{20}{100}\) + \(\frac{42}{100}\) = \(\frac{62}{100}\)
\(\frac{62}{100}\) = 0.62 in decimal
Question 11.
\(\frac{6}{10}\) + \(\frac{19}{100}\) = _________________
Answer: \(\frac{79}{100}\) = 0.79
In order to make the denominators of both fractions same for addition, multiply and divide \(\frac{6}{10}\) by 10. Then, it becomes \(\frac{60}{100}\)
Now, \(\frac{60}{100}\) + \(\frac{19}{100}\) = \(\frac{79}{100}\)
\(\frac{79}{100}\) = 0.79 in decimal
Question 12.
\(\frac{3}{10}\) + \(\frac{35}{100}\) = _________________
Answer: \(\frac{65}{100}\) = 0.65
In order to make the denominators of both fractions same for addition, multiply and divide \(\frac{3}{10}\) by 10. Then, it becomes \(\frac{30}{100}\)
Now, \(\frac{30}{100}\) + \(\frac{35}{100}\) = \(\frac{65}{100}\)
\(\frac{65}{100}\) = 0.65 in decimal
Problem Solving
For Exercises 13 and 14, write each answer as a fraction with a denominator of 100 and as a decimal.
Question 13.
Marisa walked her dog \(\frac{1}{10}\) mile on Saturday and \(\frac{55}{100}\) mile on Sunday. How far did she walk her
dog in all?

Answer: \(\frac{65}{100}\) = 0.65
Number of miles walked by Marisa’ dog on saturday = \(\frac{1}{10}\) mile
Number of miles walked by Marisa’ dog on sunday= \(\frac{55}{100}\) mile
In order to make the denominators of both fractions same for addition, multiply and divide \(\frac{1}{10}\) by 10. Then, it becomes \(\frac{10}{100}\)
Now, \(\frac{10}{100}\) + \(\frac{55}{100}\) = \(\frac{65}{100}\)
Therefore, total miles walked by Marisa’s dog = \(\frac{65}{100}\) = 0.65 in decimal
Question 14.
Nevaeh read \(\frac{2}{10}\) of a book. Her older sister read \(\frac{60}{100}\) of the same book. How much of the book did they read altogether?
Answer: \(\frac{80}{100}\) = 0.80 = 0.8
Nevaeh read \(\frac{2}{10}\) of a book
Her older sister read \(\frac{60}{100}\) of the same book.
In order to make the denominators of both fractions same for addition, multiply and divide \(\frac{2}{10}\) by 10. Then, it becomes \(\frac{20}{100}\)
Now, \(\frac{20}{100}\) + \(\frac{60}{100}\) = \(\frac{80}{100}\)
Therefore, they read \(\frac{80}{100}\) of the book altogether, which is 0.80 in decimal
Question 15.
Mathematical PRACTICE Use Algebra Find the unknown in the number sentence ![]()
Answer: 11
\(\frac{3}{10}\) + \(\frac{?}{100}\) = \(\frac{41}{100}\)
\(\frac{?}{100}\) = \(\frac{41}{100}\) – \(\frac{3}{10}\)
Make sure all the values in the denominators are same. In order to make the denominators same for calculation, represent \(\frac{3}{10}\) in the form of denominator 100 by multiplying and dividing it with 10. Then, it becomes \(\frac{30}{100}\)
Now, replace \(\frac{3}{10}\) with \(\frac{30}{100}\) in the equation for calculation
\(\frac{?}{100}\) = \(\frac{41}{100}\) – \(\frac{30}{100}\)
= \(\frac{41 – 30}{100}\)
= \(\frac{11}{100}\)
Therefore, the missing number is 11 in the given equation.
HOT Problems
Question 16.
Mathematical PRACTICE Explain to a Friend Refer to Exercise 15. Explain to a friend or classmate how you found the unknown.
Answer: To find the unknown number, simplify the steps in the following way.
Step 1: Move \(\frac{3}{10}\) from Left side of the equation to right side, in order to make unknown equation as subject.
\(\frac{?}{100}\) = \(\frac{41}{100}\) – \(\frac{3}{10}\)
Step 2: Make sure all the values in the denominators are same. In order to make the denominators same for calculation, represent \(\frac{3}{10}\) in the form of denominator 100 by multiplying and dividing it with 10. Then, it becomes \(\frac{30}{100}\)
Step 3: Now, replace \(\frac{3}{10}\) with \(\frac{30}{100}\) in the equation for calculation
latex]\frac{?}{100}[/latex] = \(\frac{41}{100}\) – \(\frac{30}{100}\)
= \(\frac{41 – 30}{100}\)
= \(\frac{11}{100}\)
Step 4: Now, compare the both equations on left and right side for the conclusion.
Therefore, the missing number is 11 in the given equation.
Question 17.
Building on the Essential Question How does place value help when adding \(\frac{1}{10}\) and \(\frac{1}{100}\)?
Answer: \(\frac{1}{10}\) can be noted as 1 tenth, which is 0.1 and \(\frac{1}{100}\) can be noted as 1 hundredth, which is 0.01.
Place value represents the position of a digit in the number. The digits followed by decimal point are noted in tenth’s place, hundredth’s place, thousandth’s place and so on.
McGraw Hill My Math Grade 4 Chapter 10 Lesson 6 My Homework Answer Key
Practice
Add. Write each sum as a fraction with a denominator of 100 and as a decimal.
Question 1.
\(\frac{2}{10}\) + \(\frac{33}{100}\) = ________________
Answer: \(\frac{53}{100}\) = 0.53
In order to make the denominators of both fractions same for addition, multiply and divide \(\frac{2}{10}\) by 10. Then, it becomes \(\frac{20}{100}\)
Now, \(\frac{20}{100}\) + \(\frac{33}{100}\) = \(\frac{53}{100}\)
\(\frac{53}{100}\) = 0.53 in decimal
Question 2.
\(\frac{6}{10}\) + \(\frac{25}{100}\) = ________________
Answer: \(\frac{85}{100}\) = 0.85
In order to make the denominators of both fractions same for addition, multiply and divide \(\frac{6}{10}\) by 10. Then, it becomes \(\frac{60}{100}\)
Now, \(\frac{60}{100}\) + \(\frac{25}{100}\) = \(\frac{85}{100}\)
\(\frac{85}{100}\) = 0.85 in decimal
Question 3.
\(\frac{4}{10}\) + \(\frac{17}{100}\) = ________________
Answer: \(\frac{57}{100}\) = 0.57
In order to make the denominators of both fractions same for addition, multiply and divide \(\frac{4}{10}\) by 10. Then, it becomes \(\frac{40}{100}\)
Now, \(\frac{40}{100}\) + \(\frac{17}{100}\) = \(\frac{57}{100}\)
\(\frac{57}{100}\) = 0.57 in decimal
Question 4.
\(\frac{2}{10}\) + \(\frac{22}{100}\) = ________________
Answer: \(\frac{42}{100}\) = 0.42
In order to make the denominators of both fractions same for addition, multiply and divide \(\frac{2}{10}\) by 10. Then, it becomes \(\frac{20}{100}\)
Now, \(\frac{20}{100}\) + \(\frac{22}{100}\) = \(\frac{42}{100}\)
\(\frac{42}{100}\) = 0.42 in decimal
Problem Solving
Mathematical PRACTICE Use Number Sense Write each answer as a fraction with a denominator of 100 and as a decimal.
Question 5.
An insect’s body is \(\frac{1}{10}\) inch long. The insect’s head is \(\frac{3}{100}\) inch long. What is the combined length of the insect’s body and head?
Answer: \(\frac{13}{100}\) = 0.13
Length of insect’s body = \(\frac{1}{10}\) inch
Length of insect’s head = \(\frac{3}{100}\) inch
In order to make the denominators of both fractions same for addition, multiply and divide \(\frac{1}{10}\) by 10. Then, it becomes \(\frac{10}{100}\)
Now, \(\frac{10}{100}\) + \(\frac{3}{100}\) = \(\frac{13}{100}\)
Therefore, total length of insect = \(\frac{13}{100}\) = 0.13 in decimal
Question 6.
Makenna rode her bike \(\frac{6}{10}\) mile in the morning and \(\frac{23}{100}\) mile in the afternoon. How far did she ride her bike in all?
Answer: \(\frac{83}{100}\) = 0.83
Makenna rode her bike \(\frac{6}{10}\) mile in the morning and \(\frac{23}{100}\) mile in the afternoon.
In order to make the denominators of both fractions same for addition, multiply and divide \(\frac{6}{10}\) by 10. Then, it becomes \(\frac{60}{100}\)
Now, \(\frac{60}{100}\) + \(\frac{23}{100}\) = \(\frac{83}{100}\)
Therefore, total distance Makenna rode her bike = \(\frac{83}{100}\) = 0.83 in decimal
Test Practice
Question 7.
Which addition expression describes the model at the right?
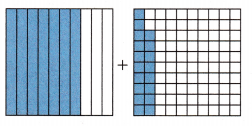
(A) \(\frac{70}{10}\) + \(\frac{18}{100}\)
(B) \(\frac{7}{10}\) + \(\frac{18}{100}\)
(C) \(\frac{7}{100}\) + \(\frac{18}{100}\)
(D) \(\frac{7}{10}\) + \(\frac{18}{10}\)
Answer: B (\(\frac{7}{10}\) + \(\frac{18}{100}\))
As, there are 7 blue parts colored out of 10, which is \(\frac{7}{10}\). Similarly, there are 18 colored parts out of 100, which is \(\frac{18}{100}\)