All the solutions provided in McGraw Hill My Math Grade 4 Answer Key PDF Chapter 10 Lesson 5 Decimals and Fractions will give you a clear idea of the concepts.
McGraw-Hill My Math Grade 4 Answer Key Chapter 10 Lesson 5 Decimals and Fractions
Decimals and fractions can show equivalent amounts. You can write equivalent fractions and you can also write fractions as decimals.
Math in My World
Example 1
Kara travels \(\frac{7}{10}\) mile from her bus stop to the next stop. Write \(\frac{7}{10}\) as a fraction with a denominator of 100. Then write the fraction as a decimal.

Use a model to show \(\frac{7}{10}\).
1. Write as a fraction with a denominator of 100.
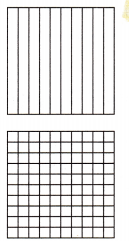
Shade seven tenths of the tenths grid.
On the hundredths grid, shade squares so that the same fraction of the two grids is shaded.
How many squares did you shade on the hundredths grid? ______________
The decimal models show that \(\frac{7}{10}\) is equivalent to \(\frac{70}{100}\).
2. Write the fraction as a decimal.
Think of \(\frac{7}{10}\) as seven tenths. So, \(\frac{7}{10}\) = 0.7.

So, \(\frac{7}{10}\) can be written as \(\frac{70}{100}\) and 0.7.
Answer:
1) 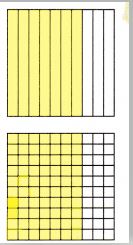
\(\frac{7}{10}\) = \(\frac{70}{100}\) = 0.70
Since 1 tenth is equal to 10 hundredths, 7 tenths is equal to 70 hundredths. You could also find the equivalent fraction by multiplying the numerator and denominator by 10.
7 tenths is represented using 7 yellow parts out of 10 parts. And, 70 hundredths is represented using 70 yellow parts out of 100 parts.
How many squares did you shade on the hundredths grid? 70
2) \(\frac{7}{10}\) = 0.7
Example 2
Write \(\frac{9}{10}\) as an equivalent fraction with a denominator of 100 and as a decimal.
Use a model to show \(\frac{9}{10}\).
1. Write \(\frac{9}{10}\) as a fraction with a denominator of 100.

Shade nine tenths of the tenths grid.
On the hundredths grid, shade squares so that the same fraction on the two grids is shaded.
How many squares did you shade on the hundredths grid? _____________
The decimal models show that \(\frac{9}{10}\) is equivalent to \(\frac{90}{100}\).
2. Write the fraction as a decimal.
Think of \(\frac{9}{10}\) as nine tenths. So, \(\frac{9}{10}\) = 0.9.
So, \(\frac{9}{10}\) can be written as \(\frac{90}{100}\) and 0.9.
Notice that ninety hundredths, or 0.90, ¡s the same as nine tenths, or 0.9.
Answer:
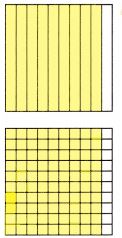
\(\frac{9}{10}\) = \(\frac{90}{100}\) = 0.90
Since 1 tenth is equal to 10 hundredths, 9 tenths is equal to 90 hundredths. You could also find the equivalent fraction by multiplying the numerator and denominator by 10.
9 tenths is represented using 9 yellow parts out of 10 parts. And, 90 hundredths is represented using 90 yellow parts out of 100 parts.
How many squares did you shade on the hundredths grid? 90
2) \(\frac{9}{10}\) = 0.9
Talk Math
Is one tenth greater than or less than one hundredth? Explain.

Answer: Tenths are larger than hundredths.
Tenths are ten times greater than hundredths.
One tenth is one part from ten equally divided a product (eg. Area). One hundredths is also one part from hundred equally divided portions of the same product (eg. area)
For instance,
\(\frac{1}{10}\) of a dollar is 10 cents or a dime.
\(\frac{1}{100}\) of a dollar is one penny.
Guided Practice
Write each fraction as an equivalent fraction with a denominator of 100. Then write the fraction as a decimal.
Question 1.
\(\frac{1}{10}\)
Fraction: 
Decimal: ______________
Answer:
Fraction: 
Since 1 tenth is equal to 10 hundredths, 1 tenths is equal to 10 hundredths. You could also find the equivalent fraction by multiplying the numerator and denominator by 10.
Decimal: 0.1
Question 2.
\(\frac{5}{10}\)
Fraction: 
Decimal: ______________
Answer:
Fraction: 
Since 1 tenth is equal to 10 hundredths, 5 tenths is equal to 10 hundredths. You could also find the equivalent fraction by multiplying the numerator and denominator by 10.
Decimal: 0.5
McGraw Hill My Math Grade 4 Chapter 10 Lesson 5 My Homework Answer Key
Practice
Question 1.
Write \(\frac{4}{10}\) as an equivalent fraction with a denominator of 100. Shade the grids to show that the fractions are equivalent. Then write the fraction as a decimal.
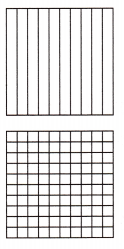
Fraction: 
Decimal: _______________
Answer:
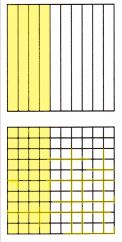
Fraction: 
Since 1 tenth is equal to 10 hundredths, 4 tenths is equal to 10 hundredths. You could also find the equivalent fraction by multiplying the numerator and denominator by 10.
4 tenths is represented using 4 yellow parts out of 10 parts. And, 40 hundredths is represented using 40 yellow parts out of 100 parts.
Decimal: 0.4
Problem Solving
Question 2.
Of Cadence’s paintbrushes, \(\frac{2}{10}\) were used to paint a picture. Write \(\frac{2}{10}\) as a fraction with a denominator of 100. Then write the fraction as a decimal.

Answer: \(\frac{2}{10}\) = \(\frac{20}{100}\) = 0.20
Since 1 tenth is equal to 10 hundredths, 2 tenths is equal to 20 hundredths. You could also find the equivalent fraction by multiplying the numerator and denominator by 10.
\(\frac{2}{10}\) = 0.2
Question 3.
Of the trees in a park, \(\frac{6}{10}\) have red leaves. Write \(\frac{6}{10}\) as a fraction with a denominator of 100. Then write the fraction as a decimal.
Answer: \(\frac{6}{10}\) = \(\frac{60}{100}\) = 0.60
Since 1 tenth is equal to 10 hundredths, 6 tenths is equal to 60 hundredths. You could also find the equivalent fraction by multiplying the numerator and denominator by 10.
\(\frac{6}{10}\) = 0.6
Question 4.
Of the menu items at a deli, \(\frac{9}{10}\) are sandwiches. Write \(\frac{9}{10}\) as a fraction with a denominator of 100. Then write the fraction as a decimal.
Answer: \(\frac{9}{10}\) = \(\frac{90}{100}\) = 0.90
Since 1 tenth is equal to 10 hundredths, 9 tenths is equal to 90 hundredths. You could also find the equivalent fraction by multiplying the numerator and denominator by 10.
\(\frac{9}{10}\) = 0.9
Question 5.
Mathematical PRACTICE Find the Error Marjorie wrote the fraction \(\frac{7}{10}\) as a fraction with a denominator of 100. She then wrote the fraction as a decimal. Find and correct her mistake. Explain.
\(\frac{7}{10}\) = \(\frac{7}{100}\)
= 0.07
Answer: \(\frac{7}{10}\) = \(\frac{70}{100}\) = 0.70
Since 1 tenth is equal to 10 hundredths, 7 tenths is equal to 70 hundredths. You could also find the equivalent fraction by multiplying the numerator and denominator by 10.
Test Practice
Question 6.
Which fraction is equivalent to \(\frac{8}{10}\)?
(A) \(\frac{8}{100}\)
(B) \(\frac{80}{100}\)
(C) \(\frac{8}{1}\)
(D) \(\frac{80}{10}\)
Answer: B (\(\frac{80}{100}\))
Since 1 tenth is equal to 10 hundredths, 8 tenths is equal to 80 hundredths. You could also find the equivalent fraction by multiplying the numerator and denominator by 10.