Into Math Grade 8 Module 7 Lesson 3 Answer Key Solve Systems by Substitution

We included HMH Into Math Grade 8 Answer Key PDF Module 7 Lesson 3 Solve Systems by Substitution to make students experts in learning maths.

HMH Into Math Grade 8 Module 7 Lesson 3 Answer Key Solve Systems by Substitution

I Can solve systems of equations by substitution.

Spark Your Learning
A state fair offers two pricing plans. Each includes a flat fee for admission and a price per ride. The equations in the table show the total cost y, in dollars, to attend the fair and go on x rides. For how many rides do the two pricing plans cost the same? Solve this problem without graphing and explain your reasoning.


Answer:
Given that the equations are,
Super saver y = 4x + 7
Fun pack y = 2x + 17
The total cost y, in dollars, to attend the fair and go on x rides.
Let us consider number of rides = x
In super saver equation
If x = 1 then y = 4(1) + 7 = 11
If x = 2 then y = 4(2) + 7 = 15
If x = 4 then y = 4(4) + 7 = 23
If x = 5 then y = 4(5) + 7 = 27
In Fun pack
If x = 1 then y = 2(1) + 17 = 19
If x = 2 then y = 2(2) + 17 = 21
If x = 3 then y = 2(3) + 17 = 23
If x = 4 then y = 2(4) + 17 = 25
If x = 5 then y = 2(5) + 17 = 27
For 5 rides the cost of the Super saver and the Fun pack is the same.

Turn and Talk How can you check that you correctly found a solution to a system of linear equations?

Build Understanding

1.
Solve the system.

A. Graph the system to estimate a solution.

Answer:

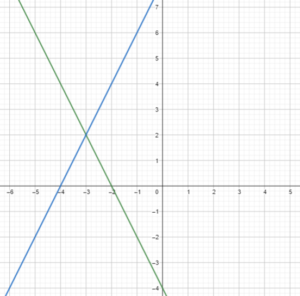
B. Since y = -2x – 4 and y = 2x + 8, what do you know about -2x – 4 and 2x + 8 at the intersection point of the two lines?

C. Solve the equation -2x – 4 = 2x + 8.
Answer:
-2x – 4 = 2x + 8
-2x – 4 – 2x – 8 = 0
-4x – 12 = 0
-4x = 12
x = -3

D. What does the solution in Part C represent?
_____________________
_____________________

E. How can you find the value of the other variable? What is the value?
_____________________
_____________________

F. What does the y-value tell you?
_____________________
_____________________

G. Check your solution by substituting x and y back into both original equations. Show your work.

H. What is the solution to the system of equations? _____

Step It Out

2. Solve this system using substitution,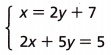

Connect to Vocabulary
To substitute is to replace a variable with a number or another expression in an algebraic expression.

A. How can you use x = 2y + 7 to substitute for x in the second equation?
Since the equation is solved for ___,
you can substitute ____ for x in the second equation.
Answer:
Since the equation is solved for y,
you can substitute y for x in the second equation.

B. Complete the following solution.
2x + 5y = 5
2(         ) + 5y = 5
____ + 5y = 5
___ + 14 = 5
9y = ___
y = ____
Answer:
2x + 5y = 5
2(2y + 7) + 5y = 5
4y + 14 + 5y = 5
9y = 5 – 14
9y = -9
y = -9/9
y = -1

C. Since y = ___, x = 2 (         ) + 7,
So, x = ____ + 7 or ___.
The solution is ____.
Answer:
Since y = -1, x = 2(-1) + 7
So, x = -2 + 7 or 5
The solution is 5.

3. For admission to a concert at the state fair, child tickets cost x dollars and adult tickets cost y dollars. Solve the system shown to find the price of each type of ticket.

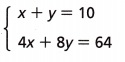
A. Solve the system by first solving for x in the first equation. Then substitute the resulting expression in the second equation and solve for one of the variables.
Since x + y = 10, x = ___

Substitute into the other equation:
4x + 8y 64
4(         ) + 8y = 64
____ + 8y = 64
___ + 4y = 64
4y = ___
y = ____
Answer:
Since x + y = 10, x = 10 – y
Substitute into the other equation:
4x + 8y = 64
4(10 – y) + 8y = 64
40 – 4y + 8y = 64
40 + 4y = 64
4y = 24
y = 6

B. Since y = ___, x = 10 – ___, and x = ___. The cost of each child ticket is ___, and the cost of each adult ticket is ____.
Answer:
Since y = 6, x = 10 – 6, and x = 4. The cost of each child ticket is 4, and the cost of each adult ticket is 6.

Turn and Talk In Part B, what would change if you substituted y = 6 into 4x + 8y = 64 instead? What would remain the same?

4. Solve this system of equations.

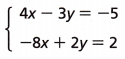
A. Solve for one of the variables in one of the equations.
4x – 3y = -5
4x = ___ – 5
x = ____
Answer:
4x – 3y = -5
4x = 3y – 5
x = 3y – 5/4

B. Make a substitution in the other equation and then solve for the variable that remains after the substitution.
Substitute x = ___ into -8x + 2y = 2. Then solve for y.
—8(____) + 2y = 2
____ + 2y = 2
___ + 10 = 2
-4y = ____
y = ____
Answer:
Substitute x = 3y – 5/4 into -8x + 2y = 2
Then solve for y
-8(3y – 5/4) + 2y = 2
-12y + 10 + 2y = 2
-10y + 10 = 2
-10y = 2 – 10
-10y = -8
y = 4/5

C. Solve for x.
Substitute y = ___ in 4x – 3y = -5. Then solve for x.
4x – 3(___) = -5
4x – ___ = -5
4x = ___
x = ____
The solution is ___.
Answer:
Substitute y = 4/5 in 4x – 3y = -5
Then solve for x
4x – 3(4/5) = -5
4x – 2.4 = -5
4x = -5 + 2.4
x = -2.6
The solution is (-2.6, 4/5).

Check Understanding

Question 1.
Describe the steps for solving a system of two equations in two variables by substitution. Explain how to check the solution.
Answer:
The steps for solving a system of two equations in two variables are
From one equation solve for x or y then.
Then the values of x or y are substituted in the second equation
Substitute the values in the equation involving both variables.

Question 2.
What is the solution to the system shown?
x – y = 3
2x – 0.5y = 0
Answer:
Given that,
The equations are
x – y = 3 is an equation 1
2x – 0.5y = 0 is an equation 2
In equation 1 x = 3 + y
Substitute x value in equation 2
2(3 + y) – 0.5y = 0
6 + 2y – 0.5y = 0
1.5y + 6 = 0
1.5y = 0 – 6
1.5y = -6
y = -4
Substitute x = -4 in equation 1
x – (-4) = 3
x + 4 = 3
x = 3 – 4
x = -1
The solution i s(-1, -4)

On Your Own

Question 3.
STEM Scientists use drones with digital cameras to help them identify plants, predict flooding, and construct 3-D maps of different landscapes. A team of scientists is using two drones to map a region. The heights of the drones are represented by the equations given, where x is the number of minutes since the drones were released by the scientists and y is the height in meters.

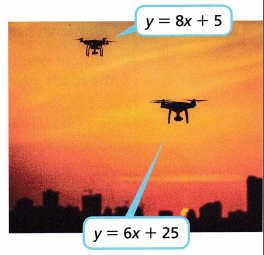
A. Solve the system of equations.
_____________________
Answer:
Given that the equations are
y = 8x + 5
y = 6x + 25
Rewrite the equations as
y – 8x = 5 is an equation 1
y – 6x = 25 is an equation 2
Substitute equation 2 from equation 1
-2x = -20
x = -20/-2
x = 10
Substitute x in equation 1
y – 8(10) = 5
y – 80 = 5
y = 5 + 80
y = 85
The solution is (10,85)

B. What does your solution tell you about the drones?
_____________________
Answer:
where x is the number of minutes since the drones were released by the scientists.
y is the height in meters.
For 10 minutes the drones were released by the scientists is 85 is meters.

Question 4.
Tickets for a school play have one price for students, x, and a different price for non-students, y. The system of equations shown is based on two different ticket orders in which the prices x and y are in dollars.
2x + 3y = 49
1 x + 2y = 30

A. What is the first step in solving the system by substitution? Justify your answer.
Answer:
Given that the equations are
2x + 3y = 49 is an equation 1
1x + 2y = 30 is an equation 2
The first step is solved for x
2x = 49 – 3y
x = 49 – 3y/2

B. Solve the system and explain what your solution represents.
Answer:
Given that the equations are
2x + 3y = 49 is an equation 1
1x + 2y = 30 is an equation 2
Multiply equation 2 with 2then we get
2x + 4y = 60 is an equation 3
Subtract equation 3 from equation 1
-y = -11
y = 11.
Substitute y in equation 1
2x + 3(11) = 49
2x + 33 = 49
2x = 49 – 33
2x = 16
x = 16/2
x = 8
The solution is (8,11)
The prize for the students is $8
The prize for the non-students is $11.

Question 5.
Consider the system of equations
2x + 5y = 18
3x + 1.5y = 9

A. Graph to estimate the solution of the system. Estimated solution: _____

Given that the equations are
2x + 5y = 18 is an equation 1
3x + 1.5y = 9 is an equation 2
From equation 1
5y = 18 – 2x
y = 18 – 2x/5
if x = 1 then y = 18 – 2(1)/5 = 3.2
If x = 2 then y = 18 – 2(2) /5 = 2.8
If x = 4 then y = 18 – 2(4)/ 5 = 10/5 = 2
If x = 5 then y = 18 – 2(5)/5 = 1.6
From equation 2
1.5y = 9 – 3x
y = 9 – 3x/1.5
If x = 1 then y = 9 – 3(1)/1.5 = 4
If x = 2 then y = 9 – 3(2)/1.5 = 2
If x = 4 then y = 9 – 3(4)/1.5 = -2
If x = 5 then y = 9 – 3(5)/1.5 = -4

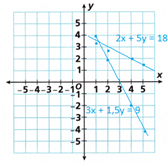
B. Solve the system by substitution.
Answer:
Given that the equations are
2x + 5y = 18 is an equation 1
3x + 1.5y = 9 is an equation 2
Multiply equation 1 with 3 and equation 2 with 2 Then we get
6x + 15y = 54 is an equation 3
6x + 3y = 18 is an equation 4
Subtract equation 4 from equation 3 then we get
12y = 36
y = 36/12
y = 3
substitute y in equation 1
2x + 5(3) = 18
2x + 15 = 18
2x = 18 – 15
2x = 3
x = 3/2
x = 1.5
The solution is (1.5, 3)

Question 6.
Complete the system of two linear equations so it has the solution (-1, 7). Check by using substitution to
solve the system.

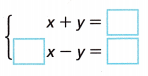
Answer:

Question 7.
The map of a small city is placed on a coordinate plane. Two of the town’s straight roads can be represented by the equations in the system shown here.
-4x – 2y = -6
2x + 2 = 7

A. Without graphing, in what quadrant of the coordinate plane do the roads intersect? How do you know?
Answer:
Given that the equations are
-4x – 2y = -6 is an equation 1
2x + 2 = 7 is an equation 2
From equation 2
2x = 7 – 2
2x = 5
x = 5/2
x = 2.5
Substitute x in equation 1
-4(2.5) – 2y = -6
-10 – 2y = -6
-2y = -6 + 10
-2y = 4
y = 4/-2
y = -2
The solution is (2.5, -2).
The points (2.5, -2) lie in the 2nd quadrant.
The lines intersect at the points (2.5, -2)

B. Attend to Precision Check your answer by graphing and labeling the equations.

For Problems 8-13, solve the system of equations.

Question 8.
3x – y = 15
x + y = 1
Answer:
Given that the equations are
x – y = 4 is an equation 1
x + 2y = 4 is an equation 2
From equation 1
x = 4 + y
Substitute x in equation 2
4 + y + 2y = 4
4 + 3y = 4
3y = 4 – 4
3y = 0
y = 0/3
y = 0
Substitute y = 0 in equation 1
x – 0 = 4
x = 4
The solution is (4,0)

Question 9.
-2x + y = 8
y = 6
Answer:
Given that the equations are
-2x + y = 8 is an equation 1
y = 6 is an equation 2
Substitute equation 2 in equation 1
-2x + 6 = 8
-2x = 8 – 6
-2x = 2
x = 2/-2
x = -1
Substitute x in equation 1
-2(-1) + y = 8
2 + y = 8
y = 8 – 2
y = 6
The solution is (-1, 6)

Question 10.
4y = 20
x – y = 7
Answer:
Given that the equations are
4y = 20 is an equation 1
x – y = 7 is an equation 2
From equation 1
y = 20/4
y = 5
Substitute y in equation 2
x – 5 = 7
x = 7 – 5
x = 2
The solution is (2,5)

Question 11.
3x – 6y = 5
2x + y = 0
Answer:
Given that the equations are
3x – 6y = 5 is an equation 1
2x + y = 0 is an equation 2
From equation 2
2x = 0 – y
x = -y/2
Substitute x in equation 1
3(-0.5y) – 6y = 5
-1.5y – 6y = 5
-7.5y = 5
y = 5/-7.5
y = -0.6
Substitute y in equation 2
2x -0.6 = 0
2x = 0 – 0.6
2x = -0.6
x = -0.6/2
x = -0.3
The solution is (-0.3, -0.6)

Question 12.
-5x + 2y = -8
2x – 3y = 12
Answer:
Given that the equations are
-5x + 2y = -8 is an equation 1
2x – 3y = 12 is an equation 2
Multiply equation 1 with 2 then we get
2(-5x + 2y) = 2(-8)
-10x + 4y = -16 is an equation 3
Multiply equation 2 with -5
-5(2x – 3y) = -5(12)
-10x + 15y = -60 is an equation 4
Subtract equation 4 from equation 3 then we get
-11y = 44
y = 44/-11
y = -4
Substitute y in equation 1
-5x + 2(-4) = -8
-5x – 8 = -8
-5x = -8 + 8
-5x = 0
x = 0/-5
x = 0
The solution is (0,-4)

Question 13.
4x + 2y = 18
-2x + 3y = 23
Answer:
Given that the equations are
4x + 2y = 18 is an equation 1
-2x + 3y = 23 is an equation 2
Multiply equation 1 with -2 and equation 2 with 4.
-8x -4y = -36 is an equation 3
-8x + 12y = 92 is an equation 4
Substitute equation 4 from equation 3
-16y = -128
y = -128/-16
y = 8
Substitute y in equation 1
4x + 2(8) = 18
4x + 16 = 18
4x = 18 – 16
4x = 2
x = 2/4
x = 1/2
x = 0.5
The solution is (0.5, 8)

I’m in a Learning Mindset!

How can I modify my process for solving systems by substitution to maintain an appropriate level of challenge?

Lesson 7.3 More Practice/Homework

Question 1.
There are x trumpet players and y saxophone players in a school’s jazz band. The equations in the system shown here relate x and y. Solve the system by substitution. What does the solution mean?
2x + 3y = 23
y = 3x – 7
Answer:
Given that the equations are
2x + 3y = 23 is an equation 1
y = 3x – 7 is an equation 2
Substitute equation 2 in equation 1
2x + 3(3x – 7) = 23
2x + 9x – 21 = 23
2x + 9x = 23 + 21
11x = 44
x = 44/11
x = 4
Substitute x in equation 2
y = 3(4) – 7
y = 12 – 7
y = 5
The solution is (4,5).

Question 2.
Students in Ms. Chu’s science class are building model rockets. Jars of baking soda cost x dollars each, and bottles of vinegar cost y dollars each. The system shown relates the prices of these items.
5x + 3y = 17
x + y = 4

A. Graph to estimate the solution of the system.

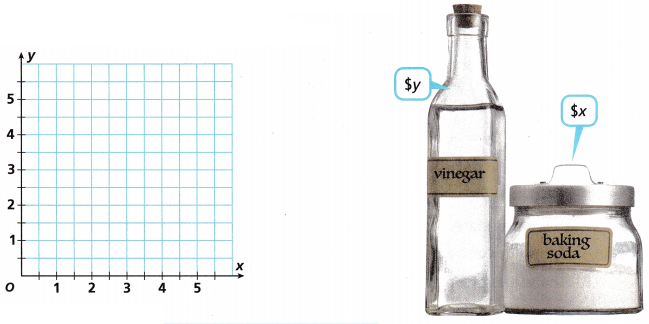
Estimated solution: ____
Answer:
Given that the equations are
5x + 3y = 17
x + y = 4
Rewrite the above equations
3y = 17 – 5x
y = 17 – 5x/3
If x = 1 then y = 17 – 5/1 = 12
If x = 2 then y = 17 – 5/2 = 6
If x = 3 then y = 17 – 5/3 = 4
x + y = 4
y = 4 – x
If x = 1 then y= 4 – 1 = 3
If x = 2 then y = 4 – 2 = 2
If x = 3 then y = 4 – 3 = 1

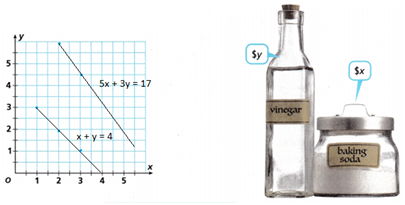
From the graph the two equations are parallel.

B. Attend to Precision Solve the system. What does the solution represent?
Answer:
Given that the equations are
5x + 3y = 17 is an equation 1
x + y = 4 is an equation 2
From equation 2
x = 4 – y
Substitute x in equation 1
5(4 – y) + 3y = 17
20 – 5y + 3y = 17
20 – 2y = 17
-2y = 17 – 20
-2y = -3
y = -3/-2
y = 1.5
Substitute y in equation 1
5x + 3(1.5) = 17
5x + 4.5 = 17
5x = 17 – 4.5
5x = 12.5
x = 12.5/5
x = 2.5
The solution is (2.5, 1.5)
The cost of backing soda is 2.5 dollars
The cost of vinegar is 1.5 dollars.

Question 3.
Use the system of equations shown for Parts A and B.

3x – 2y = -10
-4x + 3y = 13

A. Solve one of the equations for either variable.
Answer:
Given that the equations are
3x – 2y = -10 is an equation 1
-4x + 3y = 13 is an equation 2
From equation 1
3x – 2y = -10
3x = -10 + 2y
x = -10 + 2y/3
x = -3.3 + 0.6y

B. Use substitution to find the solution of the system.
Answer:
Given that the equations are
3x – 2y = -10 is an equation 1
-4x + 3y = 13 is an equation 2
Substitute x = -3.3 + 0.6y in equation 2
-4(-3.3 + 0.6y) + 3y = 13
13.2 – 2.4y + 3y = 13
0.6y + 13.2 = 13
0.6y = -0.2
y = -0.2/0.6
y = -0.3
Substitute y = -0.3 in equation 1
3x – 2(-0.3) = -10
3x + 0.6 = -10
3x = -10 – 0.6
3x = -10.6
x = -10.6/3
x = -3.53
The solution is (-3.53, -0.3)

Question 4.
Math on the Spot Solve each system by substitution.
A.
y = 3x
x + y = 3
Answer:
Given that the equations are
y = 3x is an equation 1
x + y = 3 is an equation 2
Substitute equation 1 in equation 2
x + 3x = 3
4x = 3
x = 3/4
x = 0.75
Substitute x in equation 1
y = 3(0.75)
y = 2.25
The solution is (0.85, 2.25)

B.
x – y = 4
x + 2y = 4
Answer:
Given that the equations are
x – y = 4 is an equation 1
x + 2y = 4 is an equation 2
From equation 1
x = 4 + y
Substitute x in equation 2
4 + y + 2y = 4
4 + 3y = 4
3y = 4 – 4
3y = 0
y = 0/3
y = 0
Substitute y in equation 1
x – 0 = 4
x = 4
The solution is (4,0)

Test Prep

Question 5.
Which is a correct step in solving this system of equations by substitution?
x + y = 3
3x – 4y = -5
A. Substitute x + 3 for x in the equation 3x – 4y = -5.
B. Substitute x + 3 for y in the equation 3x – 4y = -5.
C. Substitute -x + 3 for x in the equation 3x – 4y = -5.
D. Substitute -x + 3 for y in the equation 3x – 4y = -5.
Answer:
Given that the equation is
x + y = 3
3x – 4y = -5
The next step is
Substitute -x + 3 for y in the equation 3x – 4y = -5.
Option D is the correct answer.

Question 6.
Brodie is using a coordinate plane to design two straight paths in a community garden. The paths are represented by the lines 2x + 3y = 6 and -3x – 2y = 1. At what point, if any, do the two paths intersect?
Answer:
Given that the equations are
2x + 3y = 6 is an equation 1
-3x – 2y = 1. Is an equation 2
Multiply equation 1 with -3 and equation 2 with 2. Then we get
-6x – 9y = -18 is an equation 3
-6x – 4y = 2 is an equation 4
Subtract equation 4 from equation 3
-5y = -20
y = 4
Substitute y in equation 1
2x + 3(4) = 6
2x + 12 = 6
2x = 6 – 12
2x = -6
x = -6/2
x = -3
The solution is (4, -3)
The lines are intersected at the point (4, -3)

Question 7.
Celia used substitution correctly to solve one of the systems of equations shown here. As part of her solution process, she solved the equation -2x + 3(-2x + 4) = -3. Which system did Celia solve?
A. -2x + y = 4
-2x + 3y = -3
B. 2x – y = 4
-2x + 3y = -3
C. 2x + y = 4
-2x + 3y = -3
D. -2x – y = 4
-2x + 3y = -3
Answer:
Given that the solved equation is -2x + 3(-2x + 4) = -3.
A)
Given that the equations are
-2x + y = 4 is an equation 1
-2x + 3y = -3 is an equation 2
From equation 1
y = 4 + 2x
Substitute in equation 2 then we get
-2x + 3(4 + 2x) = -3

B)
Given that the equations are
2x – y = 4 is an equation 1
-2x + 3y = -3 is an equation 2
From equation 1
y = -4 + 2x
Substitute y in equation 2 then we get
-2x + 3(-4 + 2x) = -3
C)
Given that the equations are
2x + y = 4 in equation 1
-2x + 3y = -3 in equation 2
From equation 1
y = -2x + 4
Substitute y in equation 2 then we get
-2x + 3(4 – 2x) = -3
D)
Given that the equations are
-2x – y = 4 is an equation 1
-2x + 3y = -3 is an equation 2
From equation 1
y = -4 – 2x
Substitute y in equation 2 then we get
-2x + 3(-4 – 2x) = -3
Therefore option C is the correct answer.
-2x + 3(4 – 2x) = -3 is equal to the solved equation

Question 8.
Which is a true statement about the solution of this system of equations?
6x – 2y = -3
4x + 6y = 9
A. The values of both x and y are integers.
B. The values of x and y are equal.
C. The solution lies in Quadrant III of the coordinate plane.
D. The solution lies on one of the axes of the coordinate plane.
Answer:
Given that the equations are
6x – 2y = -3 is an equation 1
4x + 6y = 9 is an equation 2
Multiply equation 1 with 4 then we get
30x – 8y = -12 is an equation 1
Multiply equation 2 with 6 then we get
30x + 36y = 54 is an equation 2
Subtract equation 2 from equation 1 then we get
-44y = -66
y = -66/-44
y = 1.5
Substitute y = 1.5 in equation 1
6x – 2(1.5) = -3
6x – 3 = -3
6x = -3 + 3
6x = 0
x = 0
The solution is (0, 1.5)
The solution lies on one of the axes of the coordinate plane.
Option D is the correct answer.

Question 9.
Solve the system
2x + 3y = -9
—x + 4y = 10
Answer:
Given that the equations are
2x + 3y = -9 is an equation 1
-x + 4y = 10 is an equation 2
In equation 2
-x = 10 – 4y
x = -10 + 4y
Substitute x in equation 1
2(-10 + 4y) + 3y = -9
-20 + 8y + 3y = -9
-20 + 11y = -9
11y = -9 + 20
11y = 11
y = 1
Substitute y = 1 in equation 2
-x + 4(1) = 10
-x = 10 – 4
-x = 6
x = -6
The solution is (-6, 1).

Spiral Review

In the figure, Line m is parallel to Une n. Use the figure to solve Problems 10-12.

Question 10.
Name all of the pairs of corresponding angles in the figure.

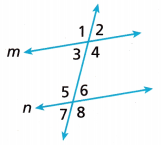
Answer:
∠2 and ∠6 are the corresponding angles
∠4 and ∠8 are the corresponding angles
∠1 and ∠5 are the corresponding angles
∠3 and ∠7 are the corresponding angles

Question 11.
The measure of ∠3 is (4x + 1)° and the measure of ∠6 is (6x – 29)°. Find the value of x and the measures of ∠3 and ∠6.
Answer:
Given,
The measure of ∠3 is (4x + 1)° and the measure of ∠6 is (6x – 29)°.
(4x + 1)° = (6x – 29)°
4x + 1 = 6x – 29
4x – 6x = -29 – 1
-2x = -30
x = 15°

Question 12.
Solve the equation 4(x + 3) + 3 = 5(x + 4).
Answer:
4(x + 3) + 3 = 5(x + 4)
4x + 12 + 3 = 5x + 20
4x + 15 – 5x – 20 = 0
-x – 5 = 0
x + 5 = 0
x = -5