We included HMH Into Math Grade 8 Answer Key PDF Module 7 Lesson 2 Solve Systems by Graphing to make students experts in learning maths.
HMH Into Math Grade 8 Module 7 Lesson 2 Answer Key Solve Systems by Graphing
I Can solve a system of linear equations by graphing and check that my solution is correct.
Spark Your Learning
Wes is laying out model train tracks along equations on a coordinate grid and wants to know if there is a place where the two trains might collide. Determine whether there is any such place, and explain your reasoning.



Turn and Talk How can you check that you correctly determined any possible places where the trains might collide?
Build Understanding
1. Gabriela is using a coordinate plane to design a race course for remote-controlled cars. She wants to use straight sections laid out according to the equations in the table. She needs to know where the cars might collide, if anywhere.

A. Graph the equations on the coordinate plane.
B. What method did you use to graph the lines?
____________________
____________________
C. Did you draw a point of intersection on the graph? Does that mean that the cars will or will not collide? Explain.
____________________
____________________
____________________
D. Are the lines you graphed parallel? How do you know?
____________________
E. What does this tell you about the two lines?
____________________
F. What can you do to graph the lines differently so that you can see the point of intersection?
____________________
____________________
____________________
G. Graph and label Gabriella’s equations, y = – x + 2 and y = -2x – 4, on the grid so that the point of intersection of the lines is shown. Draw the x- and y-axis, and indicate the scale of your graph.
H. At what point do the cars have the potential to collide? Why?
____________________
____________________
I. Compare your graph with those of other students. Did everyone make the same choices to see the point of intersection? Explain.
____________________
____________________

J. Is it possible that there is more than one point of intersection? Explain.
____________________________________
____________________________________
K. Show how you can use the coordinates of the intersection point and the given equations to check that you found the correct point.
Turn and Talk How can you tell just by looking at two given equations whether they must have a point of intersection?
Step It Out
2. When you graph a system of linear equations, the point of intersection of the lines, if any, is the solution of the system.
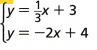
Connect to Vocabulary
A system of equations is two or more equations that contain two or more variables.
B. Estimate the solution to the system of equations.
___________________
C. Why is it difficult to determine the point of intersection from your graph directly?
___________________
___________________
D. A student claimed that the point of intersection of the lines is (\(\frac{1}{4}\), 3\(\frac{1}{2}\)). Is the student correct? How do you know?
___________________
___________________
Check Understanding
Question 1.
A city planner uses the equations y = -3x – 2 and y = x – 10 to represent two streets.
A. Graph the system. What is the point of intersection of the lines? What does it represent?
_______________________
Answer:
Given that the equations are
y = -3x – 2 is an equation 1
y = x – 10 is an equation 2
In equation 1
If x = 1 then y = -3(1) – 2 = -5
If x = 2 then y = -3(2) – 2 = -8
In equation 2
If x = 1 then y = 1 – 10 = -9
If x = 2 then y = 2 – 10 = -8
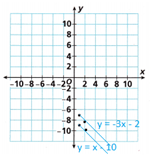
There is no point of intersection in the graph.
B. Describe how can you check your solution.
_______________________
Answer:
The equations are representing the two streets.
The first equation represents one street.
The second equation represents the second street.
On Your Own
Question 2.
STEM A laboratory incubator grows biological samples at various temperatures. A scientist uses two incubators to heat samples. In the equations, x represents the number of hours since the experiment started and y represents degrees Celsius.

A. Graph and label the equations on the coordinate plane.
Answer:
B. What is the intersection point of the lines? Explain what it represents.
Answer:
Given that,
The equations are
Incubator J is y = x + 8
Incubator k is y = 0.5x + 8
In equation 1
If x = 1 then y = 1 + 8 = 9
If x = 4 then y = 3 + 9 = 12
If x = 6 then y = 6 + 9 = 15
If x = 10 then y = 10 + 9 = 19
In equation 2
If x = 1 then y = 0.5(1) + 8 = 8.5
If x = 4 then y = 0.5(4) + 8 = 9
If x = 6 then y = 0.5(6) + 8 = 11
If x = 10 then y = 0.5(7) + 8 = 11.5
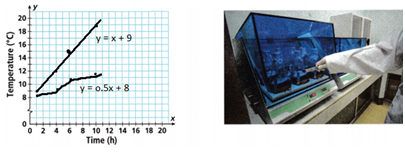
C. Explain how to check that you found the correct intersection point.
Answer:
Question 3.
The graph shows a system of equations.
A. Open Ended Write a real-world problem, including a system of equations, that could be solved by drawing the graph shown.
Answer:
The word problem is
Write an equation of the lines in the graph and the intersecting points is a solution of the graph.
B. Show how you can check that the point of intersection is a solution of the system you wrote.
Answer:
Yes, the point of intersection is the solution of the system.
The lines are intersecting at the point (-1,-1)
Question 4.
Dustin is drawing a map of Elmwood on a coordinate plane. There are two bike paths in the town.

A. Graph and label each equation on the coordinate plane.
Answer:
Given that,
Riverside path is y = -3x – 2 is an equation 1
Hilltop path is y = -1/2x + 1 = -0.5x + 1 is an equation 2
In equation 1
If x = 1 then y = -3(1) – 2 = -3 -2 = -5
If x = 2 then y = -3(2) – 2 = -6 – 2 = -8
If x = 3 then y = -3(3) – 2 = -9 – 2 = -11
In equation 2
If x = 1 then y = -0.5(1) + 1 = -0.5+ 1 = 0.5
If x = 2 then y = -0.5(2) + 1 = -1 + 1 = 0
If x = 3 then y = -0.5(3) + 1 = -1.5 + 1 = -0.5
B. Estimate the solution of the system and explain what it represents.
___________________
___________________
Answer:
Question 5.
Critique Reasoning Brianna was asked to use graphing to solve the system of equations y = 2x + 3.5 and y = 2.5x – 1.
A. Brianna said the lines are parallel and do not intersect, so the system has no solution. Do you agree or disagree? Explain.
________________
________________
________________
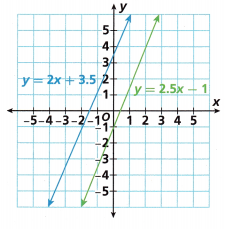
Answer:
y = 2x + 3.5 is an equation 1
If x = 1 then y = 2(1) + 3.5 = 5.5.
If x = 9 then y = 2(9) + 3.5 = 21.5
y = 2.5x – 1.is an equation 2
If x = 1 then y = 2.5(1) – 1 = 1.5
If x = 9 then y = 2.5(9) – 1 = 21.5
In the graph the two lines are parallel and they are intersecting at each other at the points of (9, 21.5)
So, the point (9. 21.5) is the solution.
B. Another student said the solution is (9, 21.5). Is he correct? Explain.
Answer:
Given that,
y = 2x + 3.5 is an equation 1
y = 2.5x – 1.is an equation 2
In the equation 1
If x = 1 then y = 2(1) + 3.5 = 5.5.
If x = 9 then y = 2(9) + 3.5 = 21.5
In the equation 2
If x = 1 then y = 2.5(1) – 1 = 1.5
If x = 9 then y = 2.5(9) – 1 = 21.5
The student said the solution is (9, 21.5).
The (9, 21.5) is the solution of the equation because at this point also the lines are intersecting at each other.
I’m in a Learning Mindset!
How was solving systems by graphing an appropriate challenge for me?
Lesson 7.2 More Practice/Homework
Question 1.
Deshawn is using a coordinate plane to design a mural. Two of the straight lines on the mural are represented by the equations y = 2x + 8 and y = \(\frac{1}{2}\)x – 4.
A. Graph and label the equations on the grid so that the point of intersection of the lines is shown.

Answer:
Given that the equations are
y = 2x + 8 is an equation 1
y = \(\frac{1}{2}\)x – 4 = 1/2x – 4
y = 0.5x – 4 is an equation 2
If x = 1 then y = 2(1) + 8 = 10
If x = 2 then y = 2(2) + 8 = 12
If x = 3 then y = 2(3) + 8 = 14
In equation 2
If x = 1 then y =0.5(1) – 4 = -3.5
If x = 2 then y = 0.5(2) – 4 = -3
If x = 3 then y = 0.5(3) – 4 = -2.5
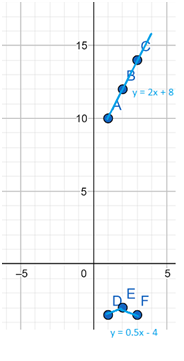
B. At what point do the lines intersect? ________________
Answer:
The two lines do not intersect because the two equations have different values.
The first equation has the positive values and the second equation has the negative values. So, they do not intersect.
C. Reason Show how you can check that the point of intersection is a solution.
Answer:
Question 2.
Model with Mathematics The total cost y of renting a paddleboat for x hours is given by y = 2x + 3 at Lake Mitchell and by y = \(\frac{1}{3}\)x + 7 at Lake Sutro.
A. Graph and label each equation on the coordinate plane.
Answer:
Given that,
The equations are
y = 2x + 3 is an equation 1
y = \(\frac{1}{3}\)x + 7 = 1/3x + 7 is an equation 2
Let us consider x = number of hours.
In equation 1
If x = 1 then y = 2(1) + 3 = 5
If x = 2 then y = 2(2) + 3 = 7
If x = 3 then y = 2(3) + 3 = 9
In equation 2
If x = 1 then y = 1/3(1) + 7 = 7.3
If x = 2 then y = 1/3(2) + 7 = 7.6
If x = 3 then y = 1/3(3) + 7 = 8
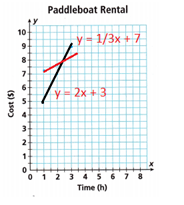
B. Estimate the solution of the system. What does the solution represent?
Answer:
The total cost of renting a paddleboat for 1 hour is 5 at Lake Mitchell.
The total cost of renting a paddleboat for 1 hour is 7.3 at Lake Sutro.
Both equations are intersecting at the point (3,8)
Question 3.
Math on the Spot Use a separate sheet of graph paper to solve each system by graphing. Check your answer.
A.
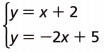
Answer:
Given that the equations are
y = x + 2 is an equation 1
y = -2x + 5 is an equation 2
In equation 1
If x = 1 then y = 1+ 2 = 3
If x = 2 then y = 2 + 2 = 4
If x = 3 then y = 3 + 2 = 5
In equation 2
If x = 1 then y = -2(1) + 5 = 3
If x = 2 then y = -2(2) + 5 = 1
If x = 3 then y = -2(3) + 5 = -1
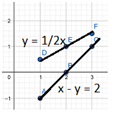
B.
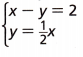
Answer:
Given that the equations are
x – y = 2
Y = 1/2x
Rewrite the above equations
-y = 2 – x
y = x – 2 is an equation 1
y = 0.5x is an equation 2
In equation 1
If x = 1 then y = 1 – 2 = -1
If x = 2 then y = 2 – 2 = 0
If x = 3 then y = 3 – 2 = 1
In equation 2
If x = 1 then y = 0.5(1) = 0.5
If x = 2 then y = 0.5(2) = 1
If x = 3 then y = 0.5(3) = 1.5
Test Prep
Question 4.
Which system of linear equations has a solution that is represented by point in Quadrant II?

Answer:
Given that
A) y = x is an equation 1
y = -x + 3 is an equation 2
Multiply equation 1 with 1 then we get
y = -x is an equation 3
Subtract equation 2 from equation 3 then we get
y = 3
Substitute y = 3 in equation 1
Then x = 3
The solution is (3,3)
B)y = x is an equation 1
y = x + 3 is an equation 2
Subtract equation 2 from equation 1 then we get
y = -3
Substitute y = -3 in equation 1
Then x = -3
The solution is (-3,-3)
C) y = -x is an equation 1
y = x + 3 is an equation 2
Subtract equation 2 from equation 1 then we get
y = 3
Substitute y = 3 in equation 1
Then x = -3
The solution is (-3,3)
D)y = -x is an equation 1
y = -x – 3 is an equation 2
Subtract equation 2 from equation 1 then we get
y = -3
Substitute y = -3 in equation 1
Then x = 3
The solution is (3,-3)
In the second quadrant x value is negative and the y value is positive.
In the second quadrant the equations is
y = -x
y = x + 3
Option c is the correct answer.
Question 5.
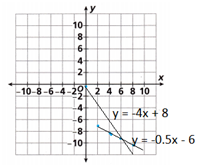
Alicia is using a coordinate plane to help her write a program for a video game. In the game, a rabbit moves along the line y = -4x + 8 and a fox moves along the line y = -0.5x – 6. Graph the two lines on the coordinate plane provided. Where do the lines intersect?
Answer:
Given that the equations is
y = -4x + 8 is an equation 1
y = -0.5x – 6 is an equation 2
In equation 1
If x = 2 then y = -4(2) + 8 = 0
If x = 4 then y = -4(4) + 8 = -8
In equation 2
If x = 2 then y = -0.5(2) – 6 = -7
If x = 4 then y = -0.5(4) – 6 = -8
If x = 6 then y = -0.5(6) – 6 = -9
Question 6.
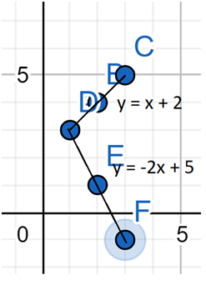
Which of the following is the solution to this system of equations?
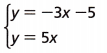
A.(-1, -3)
B. (\(-\frac{5}{8}\), \(-\frac{25}{8}\))
C. (\(-\frac{5}{2}\), \(-\frac{25}{2}\))
D. (-3, -5)
Answer:
y = -3x – 5
y = 5x
5x = -3x – 5
5x + 3x = -5
x = -5/8
Substitute x = -5/8 in y
y = 5x
y = 5(-5/8
y = -25/8
So, option B is the correct answer.
Spiral Review
Question 7.
The table gives the altitude, y, of a weather balloon, in meters, at various times, x, in minutes, since the balloon was released from a platform. Construct a function of the form y = mx + b that describes the data.
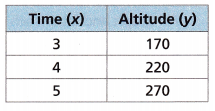
Answer:
Question 8.
Construct a linear function that has a slope of -3 and passes through the point (-2, 3).
Answer:
Given that,
The slope = -3
The points (x, y) = (-2, 3).
The linear function of two variables is always a straight line.
The standard form of the linear equation is y = mx + c
Here m = slope
y = -3x + c
3 = -3(-2) + c
3 = 6 + c
c = 3 – 6
c = -3
The equation of the straight line is y = -3x – 3.
So, the linear function is f(x) = -3x -3.
Question 9.
Solve the equation 3(x – 1) = 27 – 2x. Check your solution.
Answer:
Given that the equation is
3(x – 1) = 27 – 2x
3x – 3 = 27 – 2x
3x – 2x = 27 – 3
x = 4