Into Math Grade 8 Module 4 Lesson 2 Answer Key Investigate Angle-Angle Similarity

We included HMH Into Math Grade 8 Answer Key PDF Module 4 Lesson 2 Investigate Angle-Angle Similarity to make students experts in learning maths.

HMH Into Math Grade 8 Module 4 Lesson 2 Answer Key Investigate Angle-Angle Similarity

I Can use Angle-Angle similarity to test triangles for similarity and find unknown angle measures.

Spark Your Learning

Asa is comparing the architect’s model of a barn with the finished building. He looks at the triangle that forms the front of the roof in the model and in the completed barn. Are the triangles similar? Why or why not?

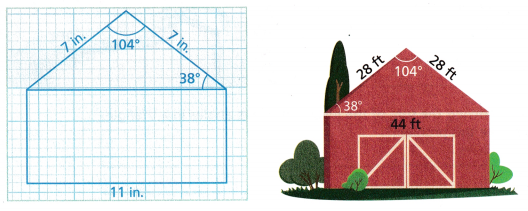
Turn and Talk Which is the easier way of deciding if the triangles are similar, comparing the angles or comparing the side lengths? Why?

Build Understanding

Two triangles are similar if all three pairs of corresponding angles are congruent. What if only two out of three pairs of corresponding angles are congruent?

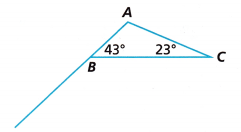
1. Using the given drawing by the set designer, Shawna is making a flag for a play. She has measured Angles ABC and C with a protractor, and they match Angles E and F, respectively, on the set designer’s notes. Can she be sure that her flag is similar to the drawing without measuring the third angle?

A. What do you know about the sum of the measures of the angles in a triangle?
___________________________
___________________________

B. How does knowing the sum of the measures of the angles in a triangle help you solve this problem?
___________________________
C. Write and evaluate an expression to find the measure of the third angle of Triangle ABC, using the angle measures given.
___________________________
D. Write and evaluate an expression to find the measure of the third angle of Triangle DEF using the angle measures given.
___________________________
E. Based on your calculation of the measure of the third angle, can you now state with confidence whether Shawna’s flag is similar to the drawing without measuring the third angle? Explain.
___________________________

The Angle-Angle Similarity Postulate states that two triangles are similar if they have two pairs of corresponding angles that are congruent.

Turn and Talk When two triangles have two angle measures in common, will the third angle measure always be the same for both triangles? Explain.

Step It Out

2. In the two triangles shown, m∠A = m∠D and m∠C = m∠F.

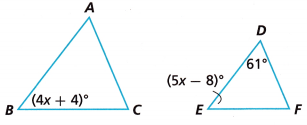
A. Do you know enough to say whether the two triangles are similar? Explain.
___________________________
___________________________

B. What does your answer to Part A imply about Angles B and E? Explain how you know.
___________________________
C. What equation can you write relating the measures of Angles B and El
___________________________
D. Solve your equation from Part C for x. What are the measures of Angles B and E? ________
___________________________
E. How can you find the measure of Angle F? ______________
___________________________
___________________________
F. How can you find the measure of Angle C?
___________________________
G. Fill in the measures of the six angles:
m∠A = ___ m∠B = ____ m∠C = ____
m∠D = ___ m∠E = ____ m∠F = ____

Turn and Talk If you were given the measures of Angles A, C, D, and E from Part G, how could you determine whether the triangles are similar?

3. The illustration shows a wheelchair ramp from the side. The support at \(\overline{B C}\) binds the ramp to the floor. Are Triangles ABC and ADE similar?

______________________
B. Do Triangles ABC and ADE both contain the same angle? If so, name it.
______________________
C. Does that mean both triangles have two pairs of corresponding congruent angles? If so, name the corresponding congruent angles.
______________________
D. Are Triangles ABC and ADE similar? Explain.
______________________

Check Understanding

Question 1.
Which two triangles are similar?

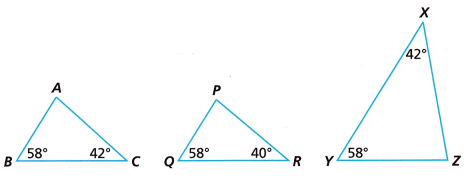
Answer:
∆ABC and ∆XYZ are similar as the angles of both the triangles are the same.
58 + 42 + x = 180
100 + x = 180
x = 180 – 100
x = 80

Question 2.
Explain why ∆XYZ is similar to ∆LMZ.

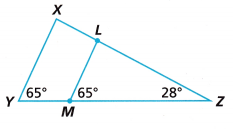
Answer: If any two angles of the triangles are the same then the triangles are said to be similar.
The angles of the given triangles ∆XYZ and ∆LMZ are the same.
Thus ∆XYZ is similar to ∆LMZ.

On Your Own

Question 3.
Reason A graphic designer wants to reproduce a logo of a mountain-climbing club for some club stationery. The logo is a triangle with the angles shown.
A. The designer wants the base to be 2 inches long. How should the triangle be drawn’
Answer:

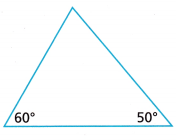
B. How can the Angle-Angle Similarity Postulate help the graphic designer make sure the triangle is reproduced correctly?
Answer:

Question 4.
Angles A, D, and G are congruent, and Angles C, F, and J are congruent.

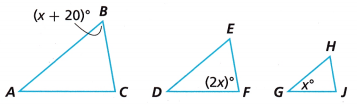
A. Write an expression to find the measures of Angles B, F, and G.
______________________

B. What is the measure of Angle E?
Answer:
Since the angles A, D, and G are congruent then the sum of given angles is equal to 180 degrees.
x + 20 + 2x + x = 180
4x + 20 = 180
4x = 180 – 20
4x = 160
x = 160/4
x = 40
Thus Angles B, E, and H are congruent.
E = x + 20
40 + 20 = 60
So Angle E = 60

Use Triangles QRS and TUV to solve Problems 5—6.

Question 5.
Are Triangles QRS and TUV similar? How do you know?

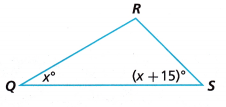
Answer: Yes Triangles QRS and TUV similar are similar as the shape of both the triangles are the same.

Question 6.
What is the measure of Angle R in terms of x?

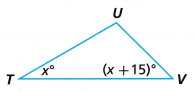
Answer:
x + (x + 15) + 90 = 180
2x + 15 + 90 = 180
2x + 105 = 180
2x = 180 – 105
2x = 75
x = 75/2
x = 37.5 degrees

Question 7.
Reason Are the triangles shown similar? Why or why not?

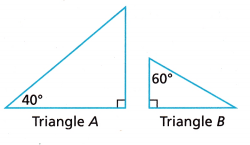
Answer: No, the angles of both the right triangles are not the same. So, the given triangles are not similar.

Question 8.
Reason Are the triangles shown similar? How do you know?

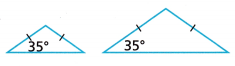
Answer: Yes both the triangles are similar as the sides of both the triangles are the same.

Question 9.
Reason Are the triangles similar? Explain.

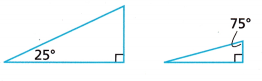
Answer: No the triangles are not similar as the angles of both the triangles are not the same.
25 + 90 + x = 180
115 + x = 180
x = 180 – 115
x = 65
65 ≠ 75

Question 10.
Angle C is congruent to Angle F. What is the measure of Angle E?

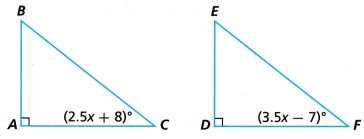
Answer:

Question 11.
Does the diagram show similar triangles? Explain.

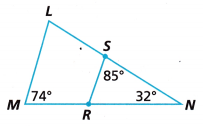
Answer: No, the triangles are not similar as the angles are not the same.

I’m in a Learning Mindset!

What can I apply from previous work with triangles to better understand whether two triangles are similar?
_______________________

Lesson 4.2 More Practice/Homework

Question 1.
One triangle shown is formed by the tree, its shadow, and a line of sight from the ground to the top of the tree. The other is formed by Manny, his shadow, and a line of sight from the ground to the top of his head.

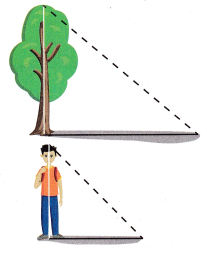
A. Are the two triangles similar? How do you know?
Answer: Yes the two triangles are similar as the shape of the triangles are the same.

B. Manny is 5\(\frac{1}{2}\) feet tall, and his shadow is 4\(\frac{1}{4}\) feet long. The shadow of the tree is 17 feet long. Can you determine the height of the tree? If so, how?
Answer:
Given,
Manny is 5\(\frac{1}{2}\) feet tall, and his shadow is 4\(\frac{1}{4}\) feet long. The shadow of the tree is 17 feet long.
4.25 ÷ 5.5 = 17 ÷ x
0.77 = 17/x
x = 17/0.77
x = 22 feet
Thus the height of the tree is 22 feet.

C. What is the height of the tree?
Answer:
The height of the tree is 22 feet.

Question 2.
Reason Are the triangles similar? Explain.

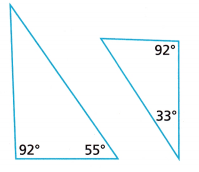
Answer:
Yes both the triangles are similar as the angles are the same.

Question 3.
Consider the diagram for Parts A and B.
A. The value of x is ___.
Answer:

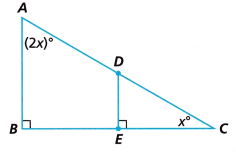
90 + 2x + x = 180
90 + 3x = 180
3x = 180 – 90
3x = 90
x = 90/3
x = 30
Thus the value of x is 30.

B. The measure of Angle A is ____
Answer:
∠BAC = 2x
Substitute the value of x.
2(30) = 60
The measure of Angle A is 60°

Test Prep

Question 4.
Angle L is congruent to Angle P, and Angle N is congruent to Angle R. What is the measure of Angle 0?

Answer:
Angle L is congruent to Angle P, and Angle N is congruent to Angle R.
∠L = 45 (ΔLMN ∼ ΔPQR)
∠R = 20 (ΔLMN ∼ ΔPQR)
45 + 20 + ∠Q = 180
m∠Q = 180 – 65
m∠Q = 115

Question 5.
Name the triangles that are similar.

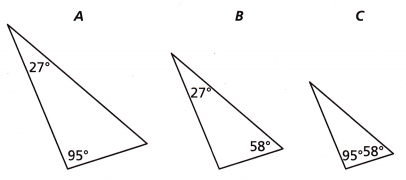
Answer:
triangle A:
95 + 27 + x = 180
122 + x = 180
x = 180 – 122
x = 58
triangle B:
27 + 58 + y = 180
85 + y = 180
y = 180 – 85
y = 95
triangle C:
95 + 58 + z = 180
153 + z = 180
z = 180 – 153
z = 27
Triangle A, B, C are similar.

Question 6.
The measures of two pairs of corresponding angles of two triangles are 24° and 55°. Explain why the two triangles are similar.
Answer:
The measures of two pairs of corresponding angles of two triangles are 24° and 55°.
The corresponding angles of the triangle are the same.
Hence the two triangles are similar.

Spiral Review

Question 7.
Mrs. Kato has 6 bags of dried beans and a 2-pound bag of rice in one shopping bag. In another shopping bag she has a 5-pound bag of flour. The two shopping bags weigh the same amount. What is the weight of each bag of dried beans?
Answer:
Given,
Mrs. Kato has 6 bags of dried beans and a 2-pound bag of rice in one shopping bag.
In another shopping bag she has a 5-pound bag of flour.
6x + 2 = 5
6x = 5 – 2
6x = 3
x = 3/6
x = 1/2 or 0.5
Thus the weight of each bag of dried beans is 1/2 pound.

Question 8.
A triangle is dilated with scale factor 4. Write a true statement about the image and preimage of the triangle.
Answer:
The corresponding sides of the image will be 4 times as long as and parallel to the preimage sides.

Question 9.
Name a sequence of transformations that would map Figure A to Figure B.

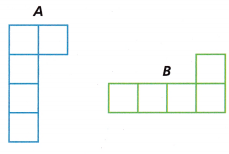
Answer:
Put A clockwise 90° to get A then put A’ rotate up 180°.