We included HMH Into Math Grade 8 Answer Key PDF Module 4 Lesson 3 Explore Parallel Lines Cut by a Transversal to make students experts in learning maths.
HMH Into Math Grade 8 Module 4 Lesson 3 Answer Key Explore Parallel Lines Cut by a Transversal
I Can identify the relationship between angle pairs as either supplementary or congruent.

Spark Your Learning
A walker sees these logs on a hike and notices that they make several angles.
Draw a representation of the logs and compare the lines and the angles in your drawing. How are the angles the same and how are they different?

Turn and Talk What pattern do you notice after measuring all the angles?
Build Understanding
When two lines are cut by a third line, the third line is called a transversal. The intersections of the lines form eight angles, including five special types of angle pairs. When the two lines cut by a transversal are parallel, as shown, the angles in any of the special pairs will be either congruent or supplementary.
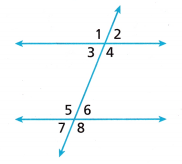
1. The term alternate means that two angles are on opposite sides of the transversal.
A. Alternate interior angles are angles on opposite sides of the transversal inside the parallel lines. Measure a pair of alternate interior angles with a protractor. Name the angles you found. Are they congruent or supplementary?
_______________________
_______________________
B. Alternate exterior angles are angles on opposite sides of the transversal outside the parallel lines. Measure a pair of alternate exterior angles with a protractor. Name the angles you found. Are they congruent or supplementary?
_______________________
_______________________
The term same-side means that two angles are on the same side of the transversal.
C. Same-side interior angles are on the same side of the transversal and between the parallel lines. Measure a pair of same-side interior angles. Name the angles you found. Are they congruent or supplementary?
_______________________
_______________________
D. Same-side exterior angles are on the same side of the transversal but outside the parallel lines. Measure a pair of same-side exterior angles. Name the angles you found. Are they congruent or supplementary?
_______________________
_______________________
E. Corresponding angles are angles in the same position formed when a third line intersects two parallel lines. Measure two pairs of corresponding angles. Name the angles you found. Are they congruent or supplementary?
_______________________
_______________________
4. You can use what you know about the angles formed by parallel lines and a transversal to prove the Triangle Sum Theorem. For any triangle, draw a line through a vertex parallel to the opposite side (in this case, through the vertex of ∠4).
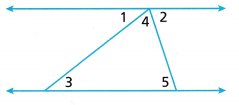
A. What is the sum of the measures of Angle 1, Angle 2, and Angle 4? How do you know?
_________________
B. How would you classify the angle pairs ∠1 and ∠3, and ∠2 and ∠5?
_________________
C. What does that tell you about their respective angle measures?
_________________
D. Complete this statement: If m∠1 = m∠3 and m∠2 = m∠5, then m∠3 + m∠4 + m∠5 = m∠![]() + m∠4 + m∠
+ m∠4 + m∠![]() =
= ![]() .
.
E. Make three copies of the triangle and arrange them so the three angles form a line. Use parallel lines and transversals to explain how your figure proves the Triangle Sum Theorem.
Check Understanding
Problems 1-2 show two parallel lines and a transversal. Find the values of x.
Question 1.
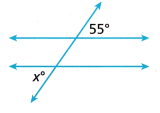
Answer:
x° = 55° (alternate exterior angles are equal)
Question 2.
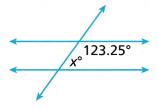
Answer:
x° + 123.25° = 180°
x = 180 – 123.25
x° = 56.75°
On Your Own
Question 3.
The picture shows a bridge between two parallel river banks. What angle does the driver’s right turn make with the river after crossing the bridge to continue on Northbridge Road?
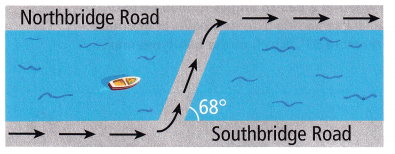
Answer:
The right angle and 68° are consecutive interior angles.
180° – 68° = 112°
So, the angle that the driver makes when he turns right is 112°
Use the diagram showing two parallel lines and a transversal to answer Problems 4-6.
Question 4.
Which angle forms a pair of alternate interior angles with ∠ACB?
Answer:
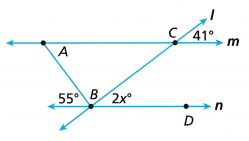
Question 5.
Which angle forms a pair of corresponding angles with the 41° angle?
Answer:
2x = 41° (corresponding angle)
x = 41/2
x = 20.5°
Question 6.
Solve for x.
Answer:
x = 20.5°
Question 7.
Reason The diagram shows two parallel lines cut by a transversal. Clarissa measured ∠1 and ∠2 with her protractor. She says the angles measure 43° and 142°, respectively. Is she correct? Explain.
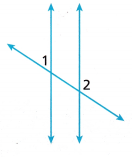
Answer:
43 + 142 = 185
The sum of two angles will not be equal to 180 degrees.
It means Clarissa is not correct.
Question 8.
In the diagram, two parallel lines are cut by a transversal. Which of the numbered angles measures 152°?
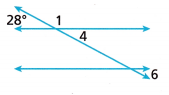
Answer:
∠1 + 28 = 180
∠1 = 180 – 28
∠1 = 152
Question 9.
Reason You’re not sure whether a pair of angles formed by two parallel lines and a transversal are same-side exterior angles or alternate exterior angles. Both angles measure 53°. Which of the two types must they be? Explain.
Answer:
Question 10.
Which two angles have the same measure?

Answer:
∠1 and ∠3 are the corresponding angles that have the same measure.
Question 11.
Lines m and n are parallel. Find the following angle pairs in the diagram. If you can’t find any, write none.
alternate exterior _____
corresponding angles ______
same-side exterior ____
alternate interior _____
same-side interior _____
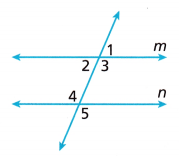
Answer:
alternate exterior: ∠4 and ∠5
corresponding angles ∠3 and ∠5
same-side exterior ∠1 and ∠5
alternate interior ∠3 and ∠4
same-side interiors ∠2 and ∠4
Question 12.
Two angles are same-side interior angles. The measures of the angles are represented by the expressions 7x + 18 and 10x + 9. What are the two angle measures?
Answer:
Given,
Two angles are same-side interior angles.
The measures of the angles are represented by the expressions 7x + 18 and 10x + 9.
Same-side interior angles = 180°
(7x + 18) + (10x + 9) = 180
17x + 27 = 180
17x = 180 – 27
17x = 153
x = 153/17 = 9
x = 9
The other angle = 10(9) + 9 = 99
I’m in a Learning Mindset!
How can I apply previous understanding of supplementary and vertical angles to find missing angles formed by parallel lines cut by a transversal?
Lesson 4.3 More Practice/Homework
Explore Parallel Lines Cut by a Transversal
Question 1.
A room in an attic has a sloping wall that makes an angle of 55° with the floor, which is parallel to the ceiling. What is the measure of an angle that forms a pair of same-side interior angles with that angle?
Answer:
Given,
A room in an attic has a sloping wall that makes an angle of 55° with the floor, which is parallel to the ceiling.
180° – 55° = 125°
So, the same side interior angle with 55° is 125°
Question 2.
Math on the Spot Line n is parallel to Line p. Find the measure of each angle.
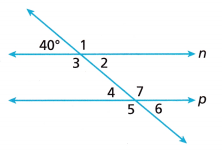
Answer:
∠1 + 40 = 180
∠1 = 180 – 40
∠1 = 140
∠1 = ∠3 (alternate angle)
∠1 = ∠3 = 140
∠2 = 40 (alternate angle)
∠1 = ∠7 (corresponding angles)
∠1 = ∠7 = 140
∠4 = 40
∠4 = ∠6 (alternate angle)
∠7 = ∠5 = 140 (alternate angle)
Question 3.
Oak Street runs parallel with Maple Street. The angle between North Main Street and West Oak Street where the turn is shown measures 65. What is the measure of the angle between the roads at the turn shown from South Main Street onto West Maple Street? Explain.
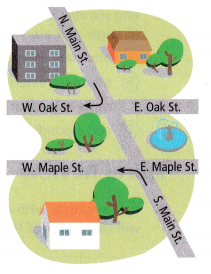
Answer:
Given,
Oak Street runs parallel with Maple Street. The angle between North Main Street and West Oak Street where the turn is shown measures 65°.
180° – 65° = 115°
Thus the angle between South Main Street and West Maple Street is 115°.
Question 4.
same-side interior angles formed have measures of (4x + 3)° and (x + 2)°.
A. How are the angles related?
_______________________
Answer: If two parallel lines are cut by a transversal, then the two same-side interior angles are equal.
B. Write and solve an equation to find the value of x.
_______________________
Answer:
(4x + 3) + (x + 2) = 180
4x + 3 + x + 2 = 180
5x + 5 = 180
5x = 180 – 5
5x = 175
x = 175/5
x = 35
C. What are the two angle measures?
_______________________
Answer:
4x + 3
4(35) + 3 = 143 degrees
Question 5.
Reason In the diagram, two parallel lines are cut by a transversal, and ∠1 and ∠6 do not form any of the kinds of angle pairs that you have learned. What is a way you can find the measure of ∠6 if you know that the measure of ∠1 is 132°? Explain.
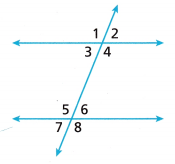
Answer:
∠1 = 132
∠1 and ∠5 are the corresponding angles
So, ∠1 = ∠5 = 132°
∠5 and ∠6 form a straight angle.
132 + ∠6 = 180
∠6 = 180 – 132
∠6 = 48°
Test Prep
Question 6.
Two parallel lines are cut by a transversal. A pair of same-side interior angles formed have measures of (2x – 11)° and (9x + 6.75)°.
What is the measure of the smaller angle?
____________
Answer:
2x – 11 + 9x + 6.75 = 180
11x – 11 + 6.75 = 180
11x – 4.25 = 180
11x = 180 + 4.25
11x = 184.25
x = 184.25/11
x = 16.75
Angle 1:
2x – 11
2(16.75) – 11
33.5 – 11 = 22.5
Angle 2:
9x + 6.75
9(16.75) + 6.75
150.75 + 6.75 = 157.50
Therefore the measure of the smaller angle is 22.5 degrees.
Question 7.
What are the values of x and y?
A. x = 30; y = 76
B. x = 76; y = 48
C. x = 80; y = 54
D. x = 132; y = 48
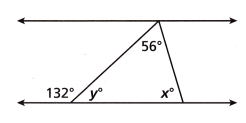
Answer:
132 + y = 180
y = 180 – 132
y = 48
48 + 56 + x = 180
104 + x = 180
x = 180 – 104
x = 76
Thus option B is the correct answer.
Question 8.
Two parallel lines are cut by a transversal. What kind of angle pair are Angles 1 and 2?
A. alternate interior angles
B. alternate exterior angles
C. same-side exterior angles
D. corresponding angles
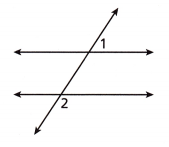
Answer:
C. same-side exterior angles
Spiral Review
Question 9.
If a unit circle with a center at (-3, 4) is reflected across the x-axis, where will the center of the reflected image lie?
_________________
Answer:
If a unit circle with a center at (-3, 4) is reflected across the x-axis.
The reflection across the x-axis is (-3, -4)
Question 10.
One triangle has angles that measure 45 and 83°. Another triangle has angles that measure 45C and 52°. Are the triangles similar? How do you know?
Answer:
Given,
One triangle has angles that measure 45 and 83°.
45 + 83 + x = 180
128 + x = 180
x = 180 – 128
x = 52
Thus the measure of the third angle is 52°
Another triangle has angles that measure 45C and 52°.
45 + 52 + y = 180
y + 97 = 180
y = 180 – 97
y = 83°
Hence the two triangles are similar.
Question 11.
An office manager is planning to set up three computer workstations and a printer in a space that is 22 feet wide. The printer takes up 4 feet.
A. Write an equation that you could use to find the width w (in feet) of the space available for each computer work station.
_______________________
Answer:
Given,
An office manager is planning to set up three computer workstations and a printer in a space that is 22 feet wide.
The printer takes up 4 feet.
w = (22-4)/3
B. What is the width of the space available for each computer work station?
_______________________
Answer:
w = (22-4)/3
w = 18/3
w = 6
