Into Math Grade 8 Module 13 Lesson 4 Answer Key Apply Volume

We included HMH Into Math Grade 8 Answer Key PDF Module 13 Lesson 4 Apply Volume to make students experts in learning maths.

HMH Into Math Grade 8 Module 13 Lesson 4 Answer Key Apply Volume

I Can use the formulas for the volumes of cones, cylinders, and spheres to solve real-world problems.

Step It Out

Question 1.
A youth sports club is holding its yearly tri-county tournament. The club is selling fruit cups in two different sizes. Fill in the missing information in the table after completing Parts A and B.


A. Find the volume of the large fruit cup to the nearest hundredth. Use the given diameter to find the radius. Use 3.14 for π.
V = πr²h r = \(\frac{d}{2}\) = = (_______)
= π (___________)² (__________)
≈ (_________) (_________) (________)
≈ __________
Answer:
Given dimensions:
height = 7 inches
diameter = 3 inches
radius = d/2 = 3/2 = 1.5
Its volume is, V = πr²h
V = 3.14 x 1.5 x 1.5 x 7
V = 49.45
The nearest hundred value is 50.

B. Find the volume of the regular fruit cup to the nearest hundredth. Substitute in the given values and simplify. Use 3.14 for π.

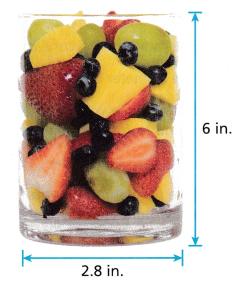
V = πr²h r = \(\frac{d}{2}\) = = (_______)
= π (___________)² (__________)
≈ (_________) (_________) (________)
≈ __________
Answer:
diameter = 2.8
r = d/2 = 2.8/2 = 1.4
The radius of the cylinder is, r = 1.4 inches
Its height is, h = 6 inches
Its volume is, V = πr²h
V = 3.14 x 1.4 x 1.4 x 6
V = 36.92
The nearest value is 37 cubic inches.

Turn and Talk Which is the better buy? Why?
Answer:
According to all measurements, we would think that the large fruit cup is better to buy.
Only small differences are there in inches.
in height 1 inch difference and in radius .5 inch difference. So if we see the measurements large one is better.

Question 2.
A paper cone cup has a height of 3.6 inches and a volume of 2.028π cubic inches.

A. What is the radius of the cone?
Use the formula for the volume of a cone. Substitute values for the volume V and the height h.

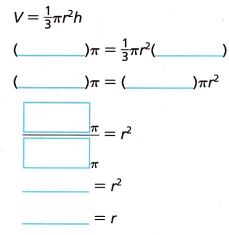
The radius of the cone is _________ inches.
Answer:
The formula to calculate the volume of a cone, given the height and its base radius is:
V = (1/3)πr²h cubic units
The given dimensions are;
height = 3.6 in
volume = 2.028π
substitute the values in the formula
2.028π = 1/3 x π x r^2 x 3.6
2.028π = 1.2 x π x r^2
2.028π/1.2π = r^2
1.69 = r^2
r = 1.3 inches
Therefore, the radius of the cone is 1.3 inches.
B. The diameter of the cone is ___________ inches.
Answer:
To find the diameter of the circle when the radius is given, you need to multiply the radius by 2.
Diameter =2*Radius
we get r = 1.3
Diameter = 2 * 1.3
Diameter = 2.6 inches
Therefore, the diameter of the cone is 2.6 inches

C. Estimate the volume of the cup in cubic inches. Use 3.14 for π and round to four decimal places.
___________ cubic inches
Answer:
The formula to calculate the volume of a cone, given the height and its base radius is:
V = (1/3)πr²h cubic units
V = 1/3 x 3.14 x 1.3 x 1.3 x 3.6
V = 6.36792
Therefore, the volume of the cup is 6.36792 cubic inches.

D. One fluid ounce of water has a volume of 1.8 cubic inches. About how many fluid ounces will the cup hold? Round your answer to the nearest tenth.
__________ fluid ounces
Answer:
volume = 1.8 cubic inches
The number of fluid ounces will the cup hold = F
for the volume we got above is 6.3
1 fluid ounce = 1.8 cubic inch

Therefore, the cup will hold 3.5 fluid ounces

Turn and Talk Why did you need to find a square root in Part A? What tools did you use to find the square root?
Answer:
We need to find out the r-value.
The formula: V = (1/3)πr²h cubic units
– Suppose, x is the square root of y, then it is represented as x=√y or we can express the same equation as x² = y. Here,’√’ is the radical symbol used to represent the root of numbers. The positive number, when multiplied by itself, represents the square of the number. The square root of the square of a positive number gives the original number.
– A square root of a number is another number that when multiplied by itself gives back the original number. Methods to find square root: 1. The method of repeated subtraction 2. Prime factorization method 3. Long division method. There are certain square root rules that need to be followed while calculating the square root. The symbol used to denote the root of a number is called radical.

Question 3.
Holly has an empty cylindrical container. She places four tennis balls, each with a diameter of 2.6 inches, inside the container. What is the approximate volume of air remaining inside the container?

A. Find the volume of the cylindrical container to the nearest hundredth. Use 3.14 for π.
V = πr²h
= π (___________)² (__________)
≈ (__________) (__________) (__________)
≈ _________ in³
Answer:
the volume of a cylinder of height ‘h’ and base radius ‘r’ is given as
Volume of a Cylinder = πr²h
Above-given dimensions are:
radius = 1.5
height = 10.5
substitute the values in the formula.
V = 3.14 x 1.5 x 1.5 x 10.5
V = 74.18
Therefore, the volume of a cylinder is 74.18 cubic inches.

B. Find the volume taken up by the four tennis balls to the nearest hundredth. Use 3.14 for π.
V = \(\frac{4}{3}\) πr³ • 4
= \(\frac{4}{3}\) π (___________)³ • 4
≈ \(\frac{4}{3}\) (_________) (_________) 4
≈ (__________) 4
≈ __________ in³
Answer:
The formula to find the volume of a sphere is given:
The volume of the sphere = 4/3 πr³ Cubic units
We know that r = 1.5
V = 4/3 x 1.5 x 1.5 x 1.5
V = 4.5cubic inches
Therefore, the volume of the sphere is 4.5 cubic inches.

C. Subtract to find the difference.
Answer:
D = volume of cylinder – volume of sphere
D = 74.18 – 4.5
D = 69.68

Check Understanding

Question 1.
Keisha is making cone-shaped snack holders for a party. The cones are 11 centimetres tall and have a radius of 6 centimetres. What is the volume of each cone? Use 3.14 for π.
Answer:
The given dimensions are:
height = 11 cm
radius = 6 cm
We need to find out the volume of the cone.
The formula to calculate the volume of a cone, given the height and its base radius is:
V = (1/3)πr²h cubic units
substitute the values in the formula
V = 1/3 x 3.14 x 36 x 11
V = 3.14 x 12 x 11
V = 414.48
Therefore, the volume of the cone is 414.48 cubic centimetres.

Question 2.
The interior of a small barrel used to store rice has a radius of 4 inches and a height of 7 inches.

A. What is the interior volume of the barrel in cubic inches? Give your answer in terms of π.
Answer:
The given dimensions are:
radius = 4 inches
height = 7 inches
It is a cylindrical shape.
the volume of a cylinder of height ‘h’ and base radius ‘r’ is given as
V = πr²h
V = π x 16 x 7
V = 112π
Therefore, the volume of the barrel in terms of π is 112π cubic inches.

B. How many scoops of rice can the barrel hold if each scoop is a hemisphere with a radius of 1 inch?
Answer:
A plane through the centre of the sphere cuts into two equal parts. Each part is called a hemisphere.
The volume of a hemisphere is half the volume of a sphere, therefore, it is expressed as,
The volume of the hemisphere = 2/3πr³, where r is the radius of the hemisphere.
r = 1
V = 2/3 x 3.14 x 1
V = 2.09
Thefeore, 2 scoops of rice a barrel can hold.

On Your Own

Question 3.
The Westhafen tower in Germany is in the shape of a cylinder. It has a height of 109 meters and a diameter of 38 meters. What is the volume of the building? Express your answer in terms of π.
Answer:
The given dimensions are:
height = 109 m
diameter = 38 m
radius = d/2 = 38/2 = 19 m
the volume of a cylinder of height ‘h’ and base radius ‘r’ is given as
V = πr²h
V = π x 19 x 19 x 109
V = 39349π
Therefore, the volume of the building in terms of π is 39349π.

Question 4.
Reason The conical cup, cylindrical cup, and hemispherical bowl shown have the same unknown radius, r. If the height of each container is the same as that radius, which of the containers holds the most liquid? Explain.

Answer:
The volume of the cone = V = (1/3)πr²h cubic units
The volume of the cylinder = V = πr²h
The volume of the hemisphere = V = 2/3πr³,
h = r
If we substitute r in the place of h then
The volume of the cone = 1/3 πr^3
The volume of the cylinder = πr^3
The volume of the hemisphere = 2/3πr^3
I think a hollow sphere can hold most liquid.

Question 5.
Attend to Precision Brady has a beach ball with a diameter of 16 inches when it is inflated. What is the volume of the beach ball, to the nearest hundredth of a cubic inch? Use 3.14 for π.
Answer:
If the sphere’s radius formed is r and the volume of the sphere is V. Then, the volume of the sphere is given by:
Volume of Sphere, V = (4/3)πr³
diameter = 16 inches
r = d/2 = 16/2 = 8 inches
V = 4/3 x 3.14 x 8 x 8 x 8
V = 2143.57333
The nearest hundred value is 2143 cubic inches.
Therefore, the volume of the beach ball is 2143 cubic units.

Question 6.
Attend to Precision A conical container can hold up to 654 cubic centimetres of sand. If the radius of the cone is 5 centimetres, what is the height of the cone? Round your answer to the nearest whole centimetre. Use 3.14 for π.
Answer:
The given dimensions are:
volume = 654 cubic cms.
radius = 5 cm
we need to find out the height of the cone.
The formula to calculate the volume of a cone, given the height and its base radius is:
V = (1/3)πr²h cubic units
Substitute the values in the formula
654 = 1/3 x 3.14 x 25 x h
654 = 27 x h
654/h = 27/1
h x 27 = 654
h = 654/27
h = 24.22
Therefore, the height of cone is 24.22 cms

Question 7.
Attend to Precision A cylindrical water tank is 7 feet tall and has a diameter of 12 feet. If the tank is currently half full, how much more water can be poured into the tank? Use \(\frac{22}{7}\) for π and round your answer to the nearest cubic foot.
Answer:
The given dimensions are:
height = 7 feet
diameter = 12
radius = d/2 = 12/2 =6 feet
The volume of the cylinder = V = πr²h
V = 3.14 x 36 x 7
V = 791.28
The tank is filled half already. The remaining place we need to find out. Let it be X.
X = 791.28/2
X = 395.64
Approximately 396 cubic foot need to fill.

Question 8.
Attend to Precision Brittany makes dough and packages it in cylindrical containers that each have a height of 4 inches. What is the radius of each container if a pack of 6 containers contains 169.56 cubic inches of dough? Use 3.14 for π and round the radius to the nearest tenth of an inch.
Answer:
The given dimensions are:
height = 4 inches
V = 169.56 cubic inches
The volume of the cylinder = V = πr²h
169.56 = 3.14 x r^2 x 4
169.56 = 12.56 x r^2
r^2 = 169.56/12.56
r^2 = 13.5
r = 3.67 inches
for 1 container , the radius is 3.67 inches
for 6 containers, the radius is R inches

Question 9.
Attend to Precision A large spherical helium balloon has a diameter of 20 feet. What is the volume of the balloon? Use 3.14 for π and express your answer in scientific notation, with the first factor rounded to the nearest hundredth.
Answer:
If the sphere’s radius formed is r and the volume of the sphere is V. Then, the volume of the sphere is given by:
Volume of Sphere, V = (4/3)πr³
diameter = 20 feet
r = d/2 = 20/2 = 10 feet
V = 4/3 x 3.14 x 10 x 10 x 10
V = 4186.666
The approximate value is 4187 cubic foot
The scientific notation is 4.18666667 × 10³

Question 10.
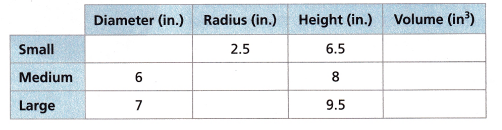
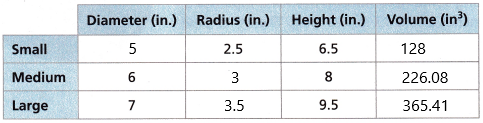
Mr. Jonas has a set of cylindrical containers. Fill in the missing information to complete the table. Round each volume to the nearest hundredth of a cubic inch. Use 3.14 for π.


Answer:
The volume of the cylinder = V = πr²h
for small cylinder:
radius = 2.5 in
height = 6.5
diameter = 2 * radius
diameter = 2 * 2.5 = 5 in
V = 3.14 x 6.25 x 6.5
V = 127.56
approximately 128 cubic inches.
for medium cylinder:
diameter = 6
r = d/2 = 6/2 = 3
height = 8
V = 3.14 x 9 x 8
V = 226.08 cubic inches
for large cylinder:
diameter = 7
r = d/2 = 7/2 = 3.5 in
height = 9.5
V = 3.14 x 3.5 x 3.5 x 9.5
V = 365.41

Question 11.
STEM One of the most common types of volcanoes is called a cinder cone volcano. These types of volcanoes are the smallest type of volcano, ranging between 300 feet and 1200 feet tall, and are in the shape of a cone. Find the volume of a cinder cone volcano with a height of 350 feet and a diameter of 1100 feet. Use 3.14 for π and round your answer to the nearest cubic foot.
Answer:
The formula to calculate the volume of a cone, given the height and its base radius is:
V = (1/3)πr²h cubic units
given units:
height = 350 feet
diameter = 1100 feet
r = d/2 = 1100/2 = 550
V = 1/3 x 3.14 x 302500 x 350
V = 110815833
The nearest number is 110000000.
Therefore, the volume of the cinder cone volcano is 110000000 cubic foot.

Question 12.
Construct Arguments Corrie wants to buy cylindrical containers to package leftover soup. The containers need to each have a volume of 66 cubic inches. To fit on a shelf, they can be no more than 6 inches tall. Would containers with a volume of 66 cubic inches and a radius of 2 inches fit? Explain.
Answer:
The given dimensions:
V = 66 cubic inches
h = 6 inches
The volume of the cylinder = V = πr²h
66 = 3.14 x r^2 x 6
66 = 18.84 x r^2
r^2 = 18.84/66
r^2 = 0.2854
r = 0.534
The radius of 2 inches is more than enough to fit.

Question 13.
Critique Reasoning A cylindrical container is three times as tall as a cone with the same diameter. Jeff says the volume of the cylinder will be three times the volume of the cone. Is Jeff correct? Explain.
Answer: it is correct.
the formula for the volume of a cone is obtained from the volume of a cylinder.
Volume of cone = (1/3) × Volume of cylinder = (1/3) × πr²h = (1/3)πr²h.

Question 14.
What is the volume of the volleyball rounded to the nearest cubic inch? Use 3.14 for π.

Answer:
If the sphere’s radius formed is r and the volume of the sphere is V. Then, the volume of the sphere is given by:
Volume of Sphere, V = (4/3)πr³
diameter = 8.15
r = d/2 = 8.15/2 = 4.075 in
V = 4/3 x 3.14 x 68
V = 285 (approximately)
Therefore, the volume of volleyball is 285 cubic inches.

Question 15.
What is the volume of the snow globe to the nearest hundredth of a cubic centimeter? Use 3.14 for π.

Answer:
If the sphere’s radius formed is r and the volume of the sphere is V. Then, the volume of the sphere is given by:
Volume of Sphere, V = (4/3)πr³
r = 7 cm
V = 4/3 x 3.14 x 343
V = 1436.
Therefore, the volume of the snow globe is 1436 cubic cms.

Question 16.
A small cylinder-shaped jar has a volume of 3.768 × 10⁵ mm³ and a height of 75 millimetres. What is the radius of the jar? Use 3.14 for π.
Answer:
The volume of the cylinder = V = πr²h
volume = 3.768 x 10^5
height = 75 mm
3.768 x 10^5 = 3.14 x r^2 x 75
376800 = 235.5 x r^2
r^2 = 376800/235.5
r^2 = 1600
r = 40 m
Therefore, the radius of the jar is 40 m

Question 17.
Bethany is installing some new water pipes. One pipe has a diameter of 1.5 inches and is 23 inches long. The other pipe has the same diameter but a length of 30 inches. How much more water can the larger pipe hold? Use 3.14 for π and round your answer to the nearest cubic inch.
Answer:
The volume of the cylinder = V = πr²h
diameter = 1.5
r = d/2 = 1.5/2 = 0.75
h = 23
V = 3.14 x 0.5625 x 23
V = 40.62 cubic inches
Therefore, the volume of the first pipe is 40.62 cubic inches.
The volume of the second pipe:
r = 0.75
h = 30
V = 3.14 x 0.5625 x 30
V = 53 (approximately)
Now subtract both volumes to know how much water did larger pipe can hold. Let it be X.
X = 53 – 40.62
X = 12.38
Therefore, the second pipe hold 12.38 more than first.

Question 18.
Lu Chen makes a large paper hat in the shape of a cone. Approximate the volume of the hat to the nearest cubic inch.
Use \(\frac{22}{7}\) for π.

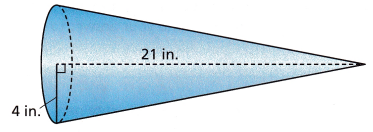
Answer:
The formula to calculate the volume of a cone, given the height and its base radius is:
V = (1/3)πr²h cubic units
height = 21 in
radius = 4 in
V = 1/3 x 3.14 x 16 x 21
V = 351.68
approximately 352
Therefore, the volume of the hat is 352 cubic inches.

Question 19.
Attend to Precision Sonia fills half of the spherical bowl shown with sand using the cylindrical scoop shown. How many scoops of sand will it take to fill half of the bowl?

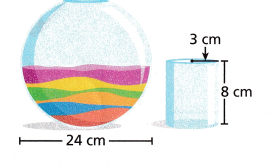
Answer:

Question 20.
A swimming pool has a radius of 8 feet and a height of 5 feet. The swimming pool is shaped like a cylinder. What is the volume of the swimming pool, to the nearest cubic foot? Use 3.14 for π.
Answer:
The given dimensions:
radius = 8 feet
height = 5 feet
The volume of the cylinder = V = πr²h
V = 3.14 x 64 x 5
V = 1004.8
approximately 1005 cubic feet.
Therefore, the volume of a swimming pool is 1005 cubic feet.

Lesson 13.4 More Practice/Homework

Question 1.
Critique Reasoning Eddie measures and finds the volume of the baseball shown. Does the approximate volume look correct? Explain.

Answer:
The diameter is given 3in
r = d/2 = 3/2 = 1.5
If the sphere’s radius formed is r and the volume of the sphere is V. Then, the volume of the sphere is given by:
Volume of Sphere, V = (4/3)πr³
V = 4/3 x 3.14 x 1.5^3
V = 14.13 cubic inches.
Eddie calculates the volume is wrong.

Question 2.
Math on the Spot Some party hats are shaped like cones. Use a calculator to find the volume of a party hat to the nearest hundredth of a cubic centimeter. If the radius of the base Is 7 centimeters and the height is 20 centimeters.

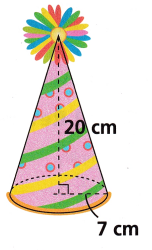
Answer:
The formula to calculate the volume of a cone, given the height and its base radius is:
V = (1/3)πr²h cubic units
the given dimensions:
h = 20cm
radius = 7 cm
V = 1/3 x 3.14 x 49 x 20
V = 1025.733
The nearest hundred’s place value is 1026 cubic cms.
Therefore, the volume of a party hat is 1026 cubic cms.

Question 3.
A grain silo is in the shape of a cylinder. The area of the circular roof is 803.84 square feet. If 13,665.28 cubic feet of grain fits in the silo, what is the height of the silo?
Answer:
The volume of the cylinder = V = πr²h
The given dimensions:
area of circle (πr^2) = 803.84
Volume = 13,665.28 cubic feet
we need to find out the height of grain.
13665.28 = 803.84 x h
h = 13665.28/803.84
h = 17 ft
Therefore, the height of the silo is 17 ft.

Question 4.
A funnel in the shape of a cone has a diameter of 4 centimetres and a height of 9 centimetres. What is the volume of the funnel, to the nearest cubic centimetre? Use 3.14 for π.
Answer:
The formula to calculate the volume of a cone, given the height and its base radius is:
V = (1/3)πr²h cubic units
diameter = 4 cm
r = d/2 = 4/2 = 2 cm
height = 9cm
V = 1/3 x 3.14 x 4 x 9
V = 1/3 x 113.04
V = 37.68
approximately 38
Therefore, the volume of the funnel is 38 cubic centimetres.

Question 5.
Art Ha-joon is a potter who makes sculptures of cylinders, spheres, and cones from clay. The diameter of each clay sphere, the diameter of the base of each clay cylinder and cone, and the height of each clay cylinder and cone are all 6 centimeters.
A. Find the volume of the clay sphere, clay cylinder, and clay cone. Leave the answers in terms of π.
sphere: ___________
cylinder: ___________
cone: ___________
Answer:
The given dimension:
height = 6cm
diameter = 6 cm
r = d/2 = 6/2 = 3cm
If the sphere’s radius formed is r and the volume of the sphere is V. Then, the volume of the sphere is given by:
Volume of Sphere, V = (4/3)πr³
V = 4/3 x π x 27
V = 36π
The volume of the cylinder = V = πr²h
V = π x 9 x 6
V = 54π
The formula to calculate the volume of a cone, given the height and its base radius is:
V = (1/3)πr²h cubic units
V = 1/3 x π x 9 x 6
V = 18π

B. How many clay spheres can Ha-Joon make if he wants to use the same amount of clay as two clay cylinders? How many clay cones can Ha-Joon make if he wants to use the same amount of clay as two clay cylinders?
Answer:
The volume of the sphere is 36π
The volume of the cylinder is 54π
The volume of the cone is 18π
For two spheres we use:
54 x 2 = 108
1 volume of sphere = 36π
the number of spheres we can make is 108/32 = 3
Therefore, we can make 3 spheres with the same amount of clay as two cylinders.
1 volume of a cone is 18π
the number of cones we can make is 108/18 = 6
Therefore, we can make 6 cones with the same amount of clay as two cylinders.

Test Prep

Question 6.
Aspherical fishbowl has a diameter of 4 inches. What is the volume of the fishbowl, to the nearest cubic inch? Use 3.14 for π.
Answer:
The given dimensions:
diameter = 4 inches
r = d/2 = 4/2 = 2
If the sphere’s radius formed is r and the volume of the sphere is V. Then, the volume of the sphere is given by:
Volume of Sphere, V = (4/3)πr³
V= 4/3 x 3.14 x 8
V = 33.49
approximately 34
therefore, the volume of the fishbowl is 34 cubic inches.

Question 7.
Alissa has an 8.2-inch-tall water bottle with a radius of 1.5 inches. Find the volume of the water bottle, rounded to the nearest hundredth of a cubic inch. Use 3.14 for π.

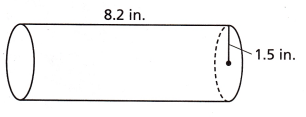
Answer:
The given dimensions:
height = 8.2 in
radius = 1.5
The volume of the cylinder = V = πr²h
v = 3.14 x 2.25 x 8.2
V = 57.933
approximately 60.
Therefore, the volume of water bottle is 60 cubic inches.

Question 8.
A waffle cone has a volume of 31.25π cubic centimetres and a radius of 2.5 centimetres. What is the approximate height of the cone?
(A) 5 cm
(B) 10 cm
(C) 15 cm
(D) 30 cm
Answer: Option C is correct.
The given dimensions:
volume = 31.25π
radius = 2.5 cm
The formula to calculate the volume of a cone, given the height and its base radius is:
V = (1/3)πr²h cubic units
31.25π = 1/3 x π x 6.25 x h
31.25 = 2.08 h
h = 31.25/2.08
h = 15cm

Spiral Review

Question 9.
Simplify.
\(\frac{7^{4} \cdot 7^{3}}{7^{5}}\) = ___________
Answer:

Question 10.
Find the unknown side length of the right triangle.

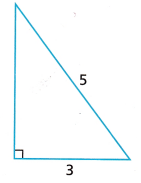
Answer:
By applying Pythagoras theorem on the cone, we can find the relation between volume and slant height of the cone.
We know, h² + r² = L²
The given dimensions:
l = 5; r = 3
Now substitute the values in the formula:
h^2 + 9 = 25
h^2 = 25 -9
h^2 = 16
h = 4
Therefore, the other side of the right triangle is 4.

Question 11.
Adrienne graphs the line y – x = 7. At what point will the line intersect the y-axis?
Answer:
When a line intersects at the y-axis, the x-coordinate will be 0.
y – 0 = 7
y = (0, 7)
The intersection of the line y-axis and the graph should be at (0,7)