Into Math Grade 8 Module 13 Review Answer Key

We included HMH Into Math Grade 8 Answer Key PDF Module 13 Review to make students experts in learning maths.

HMH Into Math Grade 8 Module 13 Review Answer Key

Vocabulary

Question 1.
Select all three-dimensional figures that have each characteristic.

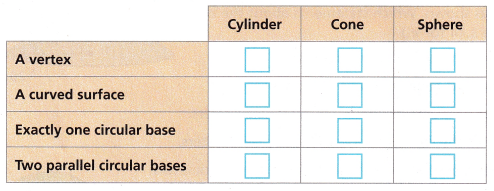
Answer:

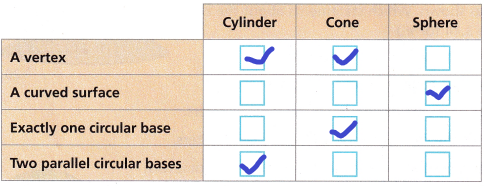
– A cylinder is a three-dimensional shape with two congruent and parallel identical bases.

Question 2.
What is the difference between the height and the slant height of a right cone?
Answer:
If slant height is $l$ and height is $h$ and radius is r
As they form right angle triangle, By applying the Pythagorean Theorem,
then, the relation between them is represented as
l^2 = h^2+r^2

Concepts and Skills

Question 3.
The cylinder shown has a radius of 8 centimeters and a height of 14 centimeters. What is the approximate volume of the cylinder? (Use \(\frac{22}{7}\) for π)

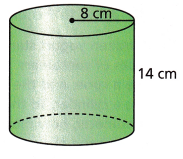
___________ cubic centimeters
Answer:
V = πr²h
given dimensions:
r = 8; h = 14
V = 22/7 x 8 x 8 x 14
V = 2813.44
Therefore, the volume of the cylinder is 2813.44 cubic cms

Question 4
A cylindrical water tank has a diameter of 10 feet and a height of 12 feet. To the nearest cubic foot, what is the volume of the water tank? (Use 3.14 for π)
(A) 942 cubic feet
(B) 1884 cubic feet
(C) 2261 cubic feet
(D) 3768 cubic feet
Answer: Option A is correct.
Explanation:
Given dimensions:
diameter = 10 ft
r = d/2 = 10/2 = 5 ft
height = 12
The formula to calculate the volume of a cylinder:
V = πr²h
V = 3.14 x 25 x 12
V = 942 cubic feet.
Therefore, the volume of a cylinder is 942 cubic feet.

Question 5.
The cylinder shown has a radius of 7 inches and a volume of 2772 cubic inches. What is the approximate height h of the cylinder? (Use \(\frac{22}{7}\) for π.)

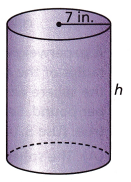
___________ inches
Answer:
Given dimensions:
radius = 7 in
volume of a cylinder = 2771 cubic inches
We need to find out the height.
The formula to calculate the volume of a cylinder:
V = πr²h
2771 = 3.14 x 49 x h
2771 = 153.86 x h
h = 153.86/2771
h = 0.0555 inches
Therefore, the height of the cylinder is 0.0555 inches.

Question 6.
Use Tools A cone has a base radius of 8.2 meters and a height of 12 meters. To the nearest cubic meter, what is the volume? (Use 3.14 for π.) State what strategy and tool you will use to answer the question, explain your choice, and then find the answer.
Answer:
Given dimensions:
radius = 8.2 m
height = 12m
We need to find out the volume of the cone.
The formula to calculate the volume of a cone, given the height and its base radius is:
V = (1/3)πr²h cubic units
V = 1/3 x 3.14 x 8.2 x 8.2 x 12
V = 844.53
Therefore, the volume of the cone is 844.53 cubic m

Question 7.
A cone-shaped pile of sand has a base diameter of 7 feet and a height of 2.4 feet, as shown. To the nearest tenth of a cubic foot, what is the volume of the pile of sand? (Use \(\frac{22}{7}\) for π.)

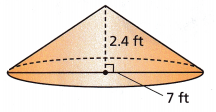
___________ cubic feet
Answer:
The formula to calculate the volume of a cone, given the height and its base radius is:
V = (1/3)πr²h cubic units
diameter = 7
radius = d/2 = 7/2 = 3.5
height = 2.4
V = 1/3 x 3.14 x 3.5 x 3.5 x 2.4
V = 30.772
Therefore, the volume of the cone is 30.772 cubic ft

Question 8.
A cone has a slant height of 25 centimetres and a radius of 20 centimetres, as shown. Which statements about the cone are correct? (Use 3.14 for π.)

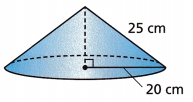
(A) The cone has a height of 32 centimetres.
(B) The height of the cone measures 15 centimetres.
(C) The cone has a volume of about 314 cubic centimetres.
(D) The volume of the cone is about 6280 cubic centimetres.
(E) The cone has a base area of about 125.6 square centimetres.
Answer: Option A is correct.
The volume of the cone in terms of slant height can be given as V = (1/3)πr²h = (1/3)πr²√(L² – r²).
By applying Pythagoras theorem on the cone, we can find the relation between volume and slant height of the cone.
We know, h² + r² = L²
⇒ h = √(L² – r²)
h = √25^2 – 20^2
h = √625 – 400
h = √225
h = 15 cms

Question 9.
A sphere has a diameter of 12 inches, as shown. To the nearest cubic inch, what is the volume of the sphere? (Use 3.14 for π.)

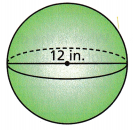
__________ cubic inches
Answer:
If the sphere’s radius formed is r and the volume of the sphere is V. Then, the volume of the sphere is given by:
Volume of Sphere, V = (4/3)πr³
radius = 12 in
Substitute the value in the formula.
V = 4/3 x 3.14 x 12 x 12 x 12
V = 4/3 x 5425.92
V = 7234.56
The nearest value is 7235 cubic inches.

Question 10.
Aspherical raindrop has a radius of 2.5 × 10^-2 centimetres. What is the approximate volume of the raindrop? (Use 3.14 for π.)
(A) 1.5 × 10^-5 cubic centimeter
(B) 2.6 × 10^-5 cubic centimeter
(C) 4.9 × 10^-5 cubic centimeter
(D) 6.5 × 10^-5 cubic centimeter
Answer:
If the sphere’s radius formed is r and the volume of the sphere is V. Then, the volume of the sphere is given by:
Volume of Sphere, V = (4/3)πr³
radius = 2.5 x 10^-2
Substitute the value in the formula.
V = 4/3 x 3.14 x (2.5 x 10^-2)^3
V = 4/3 x 3.14 x 0.0000025
V = 4/3 x 0.00000785
V = 0.0000104666667
The scientific notation is: 1.04666667 × 10^-5
The nearest value is 1.5 × 10^-5 cubic centimeter.
Therefore, option A is correct.

Question 11.
A frozen yogurt stand has two types of containers. One is shaped like a cone, and the other is shaped like a cylinder. To the nearest cubic centimeter, how much greater is the volume of the cylinder-shaped container than the cone-shaped container? (Use 3.14 for π.)

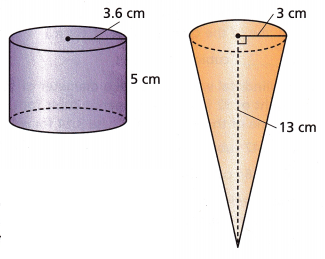
____________ cubic centimeters
Answer:
given dimensions for cone:
r = 3; h = 13
The formula to calculate the volume of a cone, given the height and its base radius is:
V = (1/3)πr²h cubic units
V = 1/3 x 3.14 x 9 x 13
V = 122.46 cubic cms
The formula to calculate the volume of a cylinder, given the height and its base radius is:
V = πr²h
given dimensions: r = 3.6, h = 5
V = 3.14 x 3.6 x 3.6 x 5
V = 203.472
To know how much greater the volume cylinder is we need to subtract. Let it be X.
X = volume of cylinder – volume of cone
X = 203.472 – 122.46
X =81.012 nothing but 81 cubic centimetres.
Therefore, 81 cubic centimetres is greater than the volume of cone.

Question 12.
A paperweight is made from a solid sphere of aluminium. The radius of the sphere is 1.75 inches. The aluminium used to make the sphere weighs 1.56 ounces per cubic inch and costs $0.90 per pound. Select all statements about the paperweight that is true. (Use 3.14 for π.)
(A) The sphere weighs about 14.4 ounces.
(B) The weight of the sphere is about 2.2 pounds.
(C) The volume of the sphere is about 16.8 cubic inches.
(D) The sphere has a volume of about 22.4 cubic inches.
(E) The aluminium used to make the sphere costs more than $5.
Answer:
r = 1.75 inches
If the sphere’s radius formed is r and the volume of the sphere is V. Then, the volume of the sphere is given by:
Volume of Sphere, V = (4/3)πr³
V = 4/3 x 3.14 x 1.75 x 1.75 x 1.75
V = 22.43
Therefore, option A is correct.