Into Math Grade 8 Module 13 Lesson 2 Answer Key Find Volume of Cones

We included HMH Into Math Grade 8 Answer Key PDF Module 13 Lesson 2 Find Volume of Cones to make students experts in learning maths.

HMH Into Math Grade 8 Module 13 Lesson 2 Answer Key Find Volume of Cones

I Can find the volume of a cone and the dimensions of a cone given its volume.

Step It Out

Question 1.
In a right cone, a line drawn from the vertex (tip) perpendicular to the base passes through the center of the base. The distance from the vertex to the center of the base is the height of the right cone.

You can use the following reasoning to develop a formula for the volume of a cone.

A. Consider a cone with radius r and height h. Imagine that the cone is made of cardboard and has an open-top, as shown. Also, consider a cylinder with the same radius and the same height.

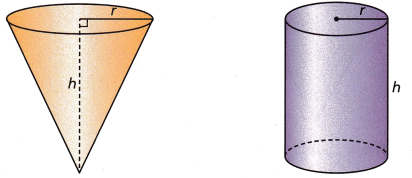
You can fill the cone with sand and pour the sand into the cylinder. It takes 3 cones full of sand to fill the cylinder completely.
This means the volume of the ___________ is \(\frac{1}{3}\) the volume of the ___________.
Answer: The volume of the cone is 1/3 the volume of the cylinder.
Explanation:
Here’s an activity to compute the volume of a cone.
– Take a conical flask and a cylindrical container of the same base radius and same height.
– Keep adding sand to the flask until it is filled to the brim. Start pouring this sand into the cylindrical container. You will observe that it does not fill up the cylinder completely.
– Again fill the conical flask with sand to the brim. Now add this sand to the cylinder, and you will observe that there is still some vacant space in the container.
– Perform this experiment yet once again. This time you will notice that the cylindrical container is entirely filled
– We can conclude from this experiment that the volume of a cylinder is thrice the volume of a cone having the same height and base radius. This implies that the volume of a cone is equal to one-third of the volume of the cylinder having the same height and base radius.
Now, you know that volume of a cylinder = πr²h
Hence,
The volume of a cone V = (1/3)πr²h cubic units.

B. Complete the following to write a formula for the volume of a cone.
volume of cone = _________ (volume of cylinder)

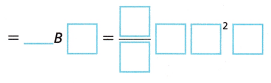
Answer:
The volume of a cone formula is given as one-third the product of the area of the circular base and the height of the cone. By measuring the height and radius of a cone, you can easily find out the volume of a cone. If the radius of the base of the cone is “r” and the height of the cone is “h”, the volume of a cone is given as V = (1/3)πr²h.
The formula to calculate the volume of a cone, given the height and its base radius is:
V = (1/3)πr²h cubic units

Turn and Talk How is the formula for the volume of a cone similar to the formula for the volume of a cylinder? How is it different?
Answer:
The formula for the volume of a cylinder is πr²h . The volume of a cone that has the same base and height is exactly one-third the volume of the cylinder. This is true for any cone that can be inscribed in a cylinder as long as the base and height are the same.

Question 2.
You can use this formula to find the volume of a cone when you know, or can calculate, its radius and height.
A. The cone-shaped party hat shown here has a radius of 3 inches. Find the volume of the cone. Use \(\frac{22}{7}\) for p.

V = \(\frac{1}{3}\) pr²h
≈ \(\frac{1}{3}\)(\(\frac{22}{7}\)) (__________)² (____________)
≈ \(\frac{1}{3}\)(\(\frac{22}{7}\)) (__________) (____________)
≈ ____________
The volume of the cone is approximately __________ cubic inches.
Answer:
The formula to calculate the volume of a cone, given the height and its base radius is:
V = (1/3)πr²h cubic units
Given r = 3 inches; height = 7 inches.
We know that the π value is 22/7 or 3.14
Now substitute the values in the formula.
V = 1/3 x 22/7 x 3 x 3 x 7
V = 1/3 x 3.14 x 9 x 7
V = 1/3 x 197.82
V = 65.94 cubic inches.
Therefore, the volume of the cone is 65.94 cubic inches.

B. Find the volume of the cone. Leave your answer in terms of p. Then approximate the volume by substituting 3.14 for p and rounding the volume to the nearest tenth.

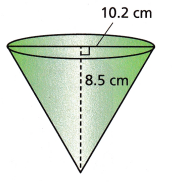
The diameter of the cone is ____________ centimeters.
So, the radius of the cone is ____________ centimeters.
V = \(\frac{1}{3}\)Bh
= \(\frac{1}{3}\) πr²h
= \(\frac{1}{3}\) π (___________)² (___________)
= ____________ π
≈ ___________
The exact volume of the cone (In terms of π) is ___________ cubic centimeters.
The volume is approximately ___________ cubic centimeters.
Answer:
Given above-information:
height = 8.5cms
diameter = 10.2 cms
radius = d/2 = 10.2/2 = 5.1 cms
The formula to calculate the volume of a cone, given the height and its base radius is:
V = (1/3)πr²h cubic units
Now substitute the values in the formula.
V = 1/3 x 3.14 x 5.1 x 5.1 x 8.5
V = 1/3 x 694.20
V = 231.40 cubic cms.
Or else we can use another formula when the diameter is given.
The formula to calculate the volume of a cone, given the measure of its height and base diameter is:
V = (1/12)πd²h cubic units.
we can substitute this formula.
height = 8.5cms
diameter = 10.2 cms
V = 1/12 x 3.14 x 10.2 x 10.2 x 8.5
V = 1/12 x 2776.82
V = 231.40 cubic cms.

Turn and Talk Why might you want to express the volume of a cone in terms of π? Why might you use 3.14 or \(\frac{22}{7}\) as an approximation for π?
Answer:

Question 3.
The slant height of a right cone is the distance from the vertex of the cone to a point on the edge of the base.
You can find the volume of a cone if you know the radius and the slant height by using properties of right triangles.

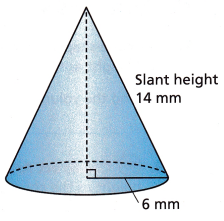
Find the approximate volume of the cone shown. Use 3.14 for π and round the volume to the nearest tenth.

A. First find the height h of the cone.
The line segments representing the height, radius, and slant height form a right triangle.
Use the Pythagorean Theorem to find h to the nearest hundredth.

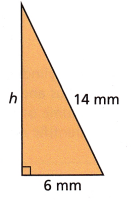
a² + b² = c²
h² + (__________)² = (__________)²
h² + __________ = __________
h² = __________
h ≈ ___________
Answer:
By applying Pythagoras theorem on the cone, we can find the relation between volume and slant height of the cone.
We know, h² + r² = L²
⇒ h = √(L² – r²)
where,
h is the height of the cone,
r is the radius of the base, and,
L is the slant height of the cone.
The volume of the cone in terms of slant height can be given as V = (1/3)πr²h = (1/3)πr²√(L² – r²).
a =h; b = r; c= l
b = 6mm; c = 14 mm
h^2 + 6^2 = 14^2
h^2 + 36 = 196
h^2 = 196 – 36
h^2 = 160
h = √160
h = 12.64 mm.
Therefore, the height of the cone is 12.64 cubic mm.

B. Next, find the approximate volume. Round to the nearest tenth.
V = \(\frac{1}{3}\) πr²h
≈ \(\frac{1}{3}\)(3.14) (_____________)² (__________)
≈ \(\frac{1}{3}\)(3.14) (___________) (__________)
≈ ___________
The volume of the cone is approximately __________ cubic millimeters.
Answer:
The formula to calculate the volume of a cone, given the height and its base radius is:
V = (1/3)πr²h cubic units
Now we know height and radius.
h = 12.64 mm; r = 6mm
V = 1/3 x 3.14 x 6 x 6 x 12.64
V = 1/3 x 1428.82
V = 476.27 cubic mm

Check Understanding

Question 1.
How do the volumes of a cone and cylinder that share a radius and height compare?
Answer:
Let’s compare the volumes of a cone with that of a cylinder by formulae and then come to the conclusive pieces of evidence.
The volume of a cone = (1/3)πr²h
The volume of the cylinder = πr²h
– both the figures that the volume of a cone is one-third of a cylinder. And the volume of a cylinder is thrice that of a cone.
– Geometrically the structural figures of a cone, a sphere, and a cylinder Having the same radii and heights occupy space in the following patterns.
– The sphere is 2/3 of the cylinder. And the cone is 1/3 of a cylinder. So the ratios of their volumes are according to the space occupied by them.

Question 2.
A. A cone has a radius of 6 inches and a slant height of 10 inches. What is the height of the cone?
Answer:
Above-given information:
radius = 6 inches
slant height L = 10 inches.
We need to find out the height of the cone.
By applying Pythagoras theorem on the cone, we can find the relation between volume and slant height of the cone.
We know, h² + r² = L²
⇒ h = √(L² – r²)
h = √(10^2 – 6^2)
h = √100 – 36
h = √64
h = 8
Therefore, the height of the cone is 8 inches.

B. What is the volume of the cone in Part A? Leave your answer in terms of π.
Answer:
Now we know,
radius = 6; height = 8
we need to find out the volume of the cone.
V = (1/3)πr²h cubic units
V = 1/3 x π x 36 x 8
V = 1/3 x π x 288
V = 96π
Therefore, the volume of the cone in terms of π is 96π cubic inches.

On Your Own

Question 3.
The cone-shaped candle to the right has a radius of 6 centimeters and height as shown.

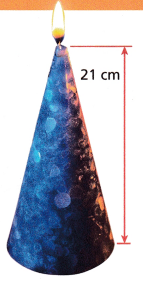
A. Find the volume of the cone. Leave your answer in terms of π.
Answer:
Above-given information:
radius = 6cms
height = 21 cms
We need to find out the volume of the cone.
The formula to calculate the volume of a cone, given the height and its base radius is:
V = (1/3)πr²h cubic units
V = 1/3 x π x 36 x 21
V = 1/3 x π x 756
V = 252π
Therefore, the volume of the cone in terms of π is 252π.

B. Construct Arguments A cylinder has the same radius and height as the cone. What is the volume of the cylinder in terms of π? Explain how you know.
Answer:

Question 4.
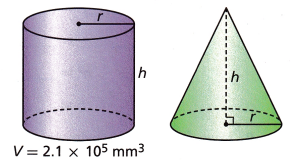
The cylinder and cone shown have the same radius and the same height. What is the volume of the cone? Give the answer in scientific notation.

Answer:
The formula to calculate the volume of a cone, given the height and its base radius is:
V = (1/3)πr²h cubic units
the volume of cylinder = πr²h
v = 2.1 x 10^5
Given that Height ($h$) and Radius($r$) are equal, $\to h=r$
the volume of a cone be V
V = 1/3 x 2.1 x 10^5
V = 1/3 x 20000
V = 70000
The scientific notation is 7 x 10^4
Therefore, the volume of the cone is 7 x 10^4 cubic mm.

For Problems 5-8, find the approximate volume of the cone. Use 3.14 for π and round the volume to the nearest tenth.

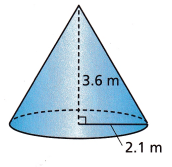
Question 5.

Answer:
Above-given information;
r = 2.1m
height = 3.6m
The formula to calculate the volume of a cone, given the height and its base radius is:
V = (1/3)πr²h cubic units
Now substitute the values in the formula.
V = 1/3 x 3.14 x 2.1 x 2.1 x 3.6
V = 1/3 x 49.85
V = 16.61
Therefore, the volume of the cone is 16.61 cubic metres.

Question 6.

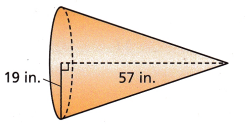
Answer:
Above-given information;
r = 19 in
height = 57 in
The formula to calculate the volume of a cone, given the height and its base radius is:
V = (1/3)πr²h cubic units
Now substitute the values in the formula.
V = 1/3 x 3.14 x 19 x 19 x 57
V = 1/3 x 64611.78
V = 21537.26
Therefore, the volume of the cone is 21537.26 cubic inches.

Question 7.

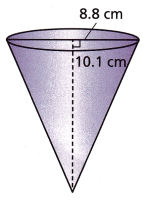
Answer:
Above-given information:
diameter = 8.8 cms
height = 10.1 cms
The formula to calculate the volume of a cone, given the measure of its height and base diameter is:
V = (1/12)πd²h cubic units.
we can substitute this formula.
V = 1/12 x 3.14 x 8.8 x 8.8 x 10.1
V = 1/12 x 2455.93
V = 204.66
Therefore, the volume of a cone is 204.66 cubic cm.

Question 8.

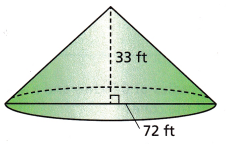
Answer:
Above-given information:
diameter = 72ft
height = 33 ft
The formula to calculate the volume of a cone, given the measure of its height and base diameter is:
V = (1/12)πd²h cubic units.
we can substitute this formula.
V = 1/12 x 3.14 x 72 x 72 x 33
V = 1/12 x 537166.08
V = 44763.84
Therefore, the volume of a cone is 44763.84 cubic ft

Use the cone-shaped hedge shown to answer Problems 9-10.

Question 9.
What is the volume of the hedge? Leave the answer in terms of π.
Answer:
Above-given information;
diameter = 6ft
r = d/2 = 6/2 = 3
r = 3 ft
height = 11ft
The formula to calculate the volume of a cone, given the height and its base radius is:
V = (1/3)πr²h cubic units
Now substitute the values in the formula.
V = 1/3 x π x 9 x 11
V = 1/3 x π x 99
V = 33π
Therefore, the volume of the hedge in terms of π is 33π.

Question 10.
Find the approximate volume of the hedge using \(\frac{22}{7}\) for π.
Round the volume to the nearest tenth
Answer:
V = 1/3 x π x 9 x 11
V = 1/3 x π x 99
V = 33 x 3.14
V = 103.62
The nearest tenth value is:
V = 103.60
Therefore, the volume of the hedge is 103.60 cubic ft.

Question 11.
The cone shown has a radius of 3 inches.
A. Reason Explain how to find the height of the cone. What is the height?
Answer:
The given dimensions are the radius of the cone = 3 inches
let the height of the cone = h inches
Substituting the values in the volume of the cone formula
Volume of cone = (1/3)πr²h
V = 1/3 x 3.14 x 9 x h
V = 9.42 x h
h = 9.42/v

B. Find the volume of the cone. Leave your answer in terms of π. Then use 3.14 for π and round the volume to the nearest tenth.
Answer:
The given dimensions are the radius of the cone = 3 inches
let the height of the cone = h inches
Substituting the values in the volume of the cone formula
Volume of cone = (1/3)πr²h
V = 1/3 x π x 9 x h
V = 3 x π x h
V =3hπ
Now substitute π value.
V = 3 x h x 3.14
V = 9.42 h
The nearest tenth values is 9.40
V = 9.42/V
V^2 = 9.42
V = √9.42
V = 3.06
The nearest tenth value is 3

For Problems 12-15, find the approximate volume of each cone. Use 3.14 for p.

Question 12.

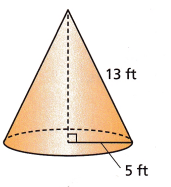
Answer:
The given dimensions are the radius of the cone = 5 ft
height = 13ft
Substituting the values in the volume of the cone formula
Volume of cone = (1/3)πr²h
The volume of the cone = 1/3 x 3.14 x 25 x 13
V = 1/3 x 1020.5
V = 340.16 cubic ft
Therefore, the volume of the cone is 340.16 cubic ft.

Question 13.

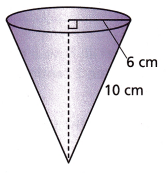
Answer:
The given dimensions are the radius of the cone = 6 cm
height = 10cm
Substituting the values in the volume of the cone formula
Volume of cone = (1/3)πr²h
The volume of the cone = 1/3 x 3.14 x 36 x 10
V = 1/3 x 1130.4
V = 376.8
Therefore, the volume of the cone is 376.8 cubic cm.

Question 14.

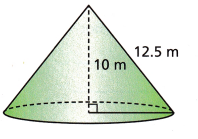
Answer:
Above-given information:
height = 10m
slant height L = 12.5m
We need to find out the radius of the cone.
By applying Pythagoras theorem on the cone, we can find the relation between volume and slant height of the cone.
We know, h² + r² = L²
⇒ r = √(L² – h²)
r = √(12.5^2 – 10^2)
r = √156.25 – 100
r = √56.25
r = 7.5
Therefore, the radius of the cone is 7.5m.

Question 15.

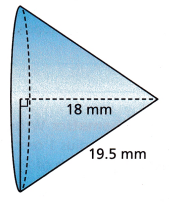
Answer:
Above-given information:
height = 18mm
slant height L = 19.5mm
We need to find out the radius of the cone.
By applying Pythagoras theorem on the cone, we can find the relation between volume and slant height of the cone.
We know, h² + r² = L²
⇒ r = √(L² – h²)
r = √(19.5^2 – 18^2)
r = √380.25 – 324
r = √56.25
r = 7.5
Therefore, the radius of the cone is 7.5mm

Question 16.
Open-Ended Determine a possible radius and height for the cone shown in the photo. Justify your answer.

Answer:

Question 17.
Critique Reasoning The cone and cylinder in the figure below have the same radius. The height of the cylinder is 3 times the height of the cone. Jared looked at the figure and concluded that the volume of the cylinder must be 3 times the volume of the cone. Therefore, he said the volume of the cylinder is 3 × 40, or 120 cubic centimeters.

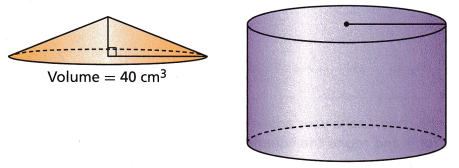
Do you agree with Jared’s reasoning? Explain.
Answer:
No, we will not agree with Jared’s reasoning.
Here is an activity that shows how the formula for the volume of a cone is obtained from the volume of a cylinder. Let us take a cylinder of height “h”, base radius “r”, and take 3 cones of height “h”. Fill the cones with water and empty out one cone at a time.
Each cone fills the cylinder to one-third quantity. Hence, such three cones will fill the cylinder. Thus, the volume of a cone is one-third of the volume of the cylinder.
Volume of cone = (1/3) × Volume of cylinder = (1/3) × πr²h = (1/3)πr²h
volume of cone = 40
40 = 1/3 x VC
40/VC = 1/3
VC = 1/3 x 40
VC = 13.33 cubic cm.

Question 18.
Consider a set of cones that all have a radius of 1 centimetre. The heights of the cones are 1 centimetre, 2 centimetres, 3 centimetres, 4 centimetres, and 5 centimetres.
A. Complete the table. Leave the volumes in terms of π.

Answer:
The formula to calculate the volume of a cone, given the height and its base radius is:
V = (1/3)πr²h cubic units
radius = 1
height = 1, 2, 3, 4, 5
V = 1/3 x 3.14 x 1 x 1 = 1.04
V = 1/3 x 3.14 x 1 x 2 = 2.09
V = 1/3 x 3.14 x 1 x 3 = 3.14
V = 1/3 x 3.14 x 1 x 4 = 4.18
V = 1/3 x 3.14 x 1 x 5 = 5.23

B. Is the relationship in the table a proportional relationship? Why or why not?
Answer:
yes, it is a proportional relationship because the volume is increasing.
– The proportional relationship is a mathematical term that indicates two or more variables.
– The proportional relationship is used to understand how an increase or decrease in one variable affects the other.
– The proportional relationship is often visually demonstrated with line graphs to increase the ease of understanding.

C. Model with Mathematics Write an equation that gives the volume y of a cone with a radius of 1 centimetre if you know the height x of the cone. Describe the graph of the equation.
Answer:

Lesson 13.2 More Practice/Homework

Question 1.
Construct Arguments What is the volume of a cylinder that has the same radius and same height as the cone fountain shown? Explain.

Answer:
The volume of the cone = 2.6 cubic metres
The formula to calculate the volume of a cone, given the height and its base radius is:
V = (1/3)πr²h cubic units
the volume of cylinder = πr²h
Given that Height ($h$) and Radius($r$) are equal, →h=r
Therefore, we can conclude that volume of cone is one third the volume of a cylinder. Given that thier height and radii are same.
Volume of cone = (1/3) × Volume of cylinder = (1/3) × πr²h = (1/3)πr²h
2.6 = 1/3πr²h
2.6 = 1/3 x VC
VC =1/3 x 2.6
Volume of cylinder = 0.8 cubic mts

Question 2.
A cone has a height of 6 × 10³ millimetres and a radius of 2 × 10³ millimetres. Find the volume of the cone. Leave your answer in scientific notation and in terms of π.
Answer:
The formula to calculate the volume of a cone, given the height and its base radius is:
V = (1/3)πr²h cubic units
height = 6 × 10³ millimetres
radius = 2 × 10³ millimetres.
V = 1/3 x π x 4000000 x 6000
after calculation we get
V = 8 x 10^9π

For Problems 3-6. approximate the volume of each cone. Use 3.14 for π and round the volume to the nearest tenth.

Question 3.

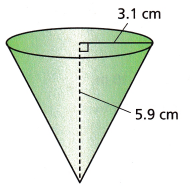
Answer:
The formula to calculate the volume of a cone, given the height and its base radius is:
V = (1/3)πr²h cubic units
radius = 3.1 cm
height = 5.9 cm
V = 1/3 x 3.14 x 3.1 x 3.1 x 5.9
V = 1/3 x 178.03
V = 59.34
The nearest tenth value is 59.30
Therefore, the volume of the cone is 59.30 cubic cm.

Question 4.

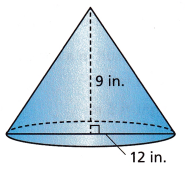
Answer:
The formula to calculate the volume of a cone, given the height and its base radius is:
V = (1/3)πr²h cubic units
height = 9 in
diameter = 12 in
r = d/2 = 12/2 = 6 in
V = 1/3 x 3.14 x 36 x 9
V = 1/3 x 1017.36
V = 339.12 cubic in
The nearest tenth value is 339.10
Therefore, the volume of the cone is 339.10 cubic in

Question 5.

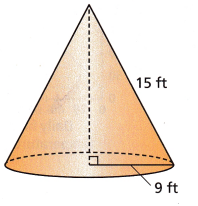
Answer:
Above-given information:
radius = 9 ft
slant height L = 15 ft
We need to find out the height of the cone.
By applying Pythagoras theorem on the cone, we can find the relation between volume and slant height of the cone.
We know, h² + r² = L²
⇒ h = √(L² – r²)
h = √(15^2 – 9^2)
h = √225-81
h = √144
h = 12
Therefore, the height of the cone is 12ft.

Question 6.

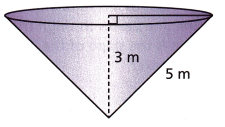
Answer:
Above-given information:
height = 3m
slant height L = 5m
We need to find out the radius of the cone.
By applying Pythagoras theorem on the cone, we can find the relation between volume and slant height of the cone.
We know, h² + r² = L²
⇒ r = √(L² – h²)
r = √(25 – 9)
r = √16
r = 4
Therefore, the radius of the cone is 4m

Question 7.
A model with Mathematics A cone has diameter d and height h. Write a formula for the volume V of the cone in terms of d and h.
Answer:
The formula to calculate the volume of a cone, given the measure of its height and base diameter is:
V = (1/12)πd²h cubic units

Test Prep

Question 8.
Fill in the formula for the volume of the cone shown here by writing a numerical value in each box.

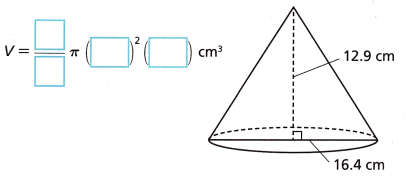
Answer:
The formula to calculate the volume of a cone, given the height and its base radius is:
V = (1/3)πr²h cubic units
diameter = 16.4 cm
r = d/2 =16.4/2 = 8.2 cm
height = 12.9 cm
V = 1/3 x π x (8.2)^2 x 12.9
V = 1/3 x 3.14 x 8.2 x 8.2 x 12.9
V = 1/3 x 2723.62
V = 907.87 cubic cm
Question 9.
A cone has a radius of 3 feet and a height of 5 feet. A cylinder has the same radius and height as the cone. Which of the following statements are true? Select all that apply.
(A) The volume of the cone is 15π ft³.
(B) The volume of the cylinder is 45π ft³.
(C) The volume of the cone is 3 times the volume of the cylinder.
(D) The volume of the cylinder is 3 times the volume of the cone.
(E) The ratio of the volume of the cone to the volume of the cylinder is \(\frac{1}{3}\).
(F) The ratio of the volume of the cylinder to the volume of the cone is \(\frac{1}{3}\).
Answer: option A and B are correct
The formula to calculate the volume of a cone, given the height and its base radius is:
V = (1/3)πr²h cubic units
V = 1/3 x π x 9 x 5
V = 1/3 x π x 45
V = 15π cubic ft.
The formula to calculate the volume of a cylinder: V = πr²h
V = π x 9 x 5
V = 45π cubic ft.

Question 10.
Which radius and height result in a cone with the least volume?
(A) radius = 7 m; height = 1 m
(B) radius = 5 m; height = 5 m
(C) radius = 3 m; height = 10 m
(D) radius = 1 m; height = 15 m
Answer: Option D is correct.
The formula to calculate the volume of a cone, given the height and its base radius is:
V = (1/3)πr²h cubic units
we can go for optional verification.
V = 1/3 x 3.14 x 49 x 1 = 51.28
V = 1/3 x 3.14 x 25 x 5 = 130.83
V = 1/3 x 3.14 x 9 x 10 = 94.2
V = 1/3 x 3.14 x 1 x 15 = 15.7
by comparing all the answers we got least value is 15.7
so, the correct answer is option D.

Spiral Review

Question 11.
Latreesha collected data on the daily high temperature and the number of quarts of iced coffee sold at a cafe. She made a scatter plot of the data and then drew a trend line, as shown. The line passes through the points (10, 50) and (30, 100). What is the slope of the line? What does it represent in this context?

Answer:
If P(x₁,y₁) and Q(x₂,y₂) are the two points on a straight line, then the slope formula is given by:
Slope, m = Change in y-coordinates/Change in x-coordinates
m = (y₂ – y₁)/(x₂ – x₁)
Given,the points P = (10, 50) and Q = (30,100).
As per the slope formula, we know that,
m = (100-50)/30-10)
m = 50/20
m = 5/2
therefore, the slope of the line is 5/2.

Question 12.
Solve the system of equations
-3x + 5y = 21
12x – 3y= -13
Answer:
-3x + 5y = 21 be the equation 1.
12x – 3y = -13 be the equation 2.
Step 1: Solve−3x + 5y = 21 for x:
−3x + 5y = 21
−3x + 5y + (−5y) = 21 + (−5y)  (Add -5y to both sides)
−3x = −5y + 21
divide both sides by -3.

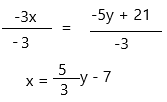
step 2: substitute ‘x’ value in 12x – 3y = -13
12x – 3y = -13

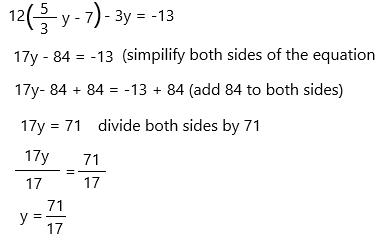
Step 3: substitute ‘y’ value in ‘x’ value.

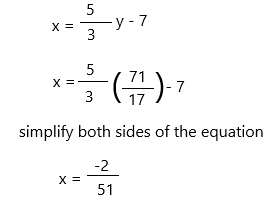
Therefore, the answer is;
x = -2/51; y = 71/17

Question 13.
Approximate the volume of a cylinder with a radius of 3.4 meters and a height of 1.2 meters. Use 3.14 for π and round the volume to the nearest tenth.
Answer:
We know that the base of a right circular cylinder is a circle and the area of a circle of radius ‘r’ is πr². Thus, the volume (V) of a right circular cylinder, using the above formula, is,
V = πr²h
The above-given dimensions are:
radius = 3.4mts
height = 1.2 mts
V = 3.14 x 3.4 x 3.4 x 1.2
V = 43.55
The nearest tenth value is 44.
Therefore, the volume of the cylinder is 44 cubic mts.