We included HMH Into Math Grade 7 Answer Key PDF Module 2 Lesson 2 Markups and Discounts to make students experts in learning maths.
HMH Into Math Grade 7 Module 2 Lesson 2 Answer Key Markups and Discounts
I Can calculate markups and markdowns.
Step It Out
1. Music Enterprise buys digital downloads of music albums for $5.00. This $5.00 is called the cost. The markup rate is 30%. How much will you pay for an album, not including tax?
Connect to Vocabulary
Markup is the amount of increase in a price. The markup rate is similar to percent increase but more
specific to selling items.
Retail price is the amount an item is sold for after a company adds the markup.
Markdown is the amount of decrease in a price.
A. The markup rate is ___%. As a decimal, it is ____
B. The original amount, or cost, is ____
C. Calculate the amount of the markup added to the cost.
____ × 5 = ___ The markup amount is $ ____.
D. Calculate the retail price after markup.
$5.00 + ___$ = $____ The retail price is $ ___.
E. Write the ratio of the retail price to the cost of the download. Express this ratio as a percent.
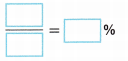
So the retail price after markup is ____% of the cost. In other words: original amount + markup = retail
100% + ___% = ___%
After New Year’s Day, Music Enterprise marks down their retail prices as shown. What will be the new retail price after this markdown?
F. The retail price is $___. The markdown is ____%.
G. Calculate the amount of the markdown.
____ × 6.50 = $_____
H. Calculate the retail price after markdown.
$6.50 – $___ = $____

Answer:
A. The markup rate is 30%. As a decimal, it is 0.3
B. The original amount, or cost, is $5.
C. Calculate the amount of the markup added to the cost.
1.3× 5 = 6.50 The markup amount is $ 6.50.
D. $5.00 + 1.5 $ = $6.50 The retail price is $ 6.50.
Turn and Talk Explain why the final retail price is lower than the original cost.
2. You can also use equations to solve problems involving markups, markdowns, and discounts.
Penelope buys bracelets in bulk at a cost of S8 each to sell at her store. She uses a markup rate of 125%, which is added to the bracelet cost. What is the retail price of a bracelet?
A. The markup rate is ____. The markup rate in decimal form is ____
Answer: The markup rate is 125%. The markup rate in decimal form is 125/100 = 1.25
B. The equation m = ___ x gives the markup amount m in dollars for the bracelets in terms of the original cost x in dollars.
Answer:
The equation m = 1.25x gives the makeup amount m in dollars for the bracelets in terms of the original cost x in dollars.
C. Use the equation to find the markup amount for a bracelet.
m = ___ × ____ m = ____
The markup amount is $___.
Answer:
m = 1.25 × 8 m = 10
The markup amount is $10.
D. Calculate the retail price of the bracelet.
cost + markup = retail price
$8 + $____ = $_____
The retail price is $___.
Answer:
cost + markup = retail price
$8 + $10= $18
The retail price is $18.
E. The markup amount is x. An equation for the retail price r in dollars in terms of the original amount x in dollars is
r = ___x + ___ x = ____x
Penelope marked down the price of necklaces in her store as shown. Find the markdown rate of the sale price.
F. Write the ratio of the sale price to the original retail price. Express this ratio as a percent.

G. Think of the original retail price of the necklace as 100%. How does the sale price compare to the retail price of the necklace? What does this tell you about the markdown rate?

H. What is an equation in the form y = kx that relates the sale price to the retail price x? ___________
Turn and Talk Discuss how you find the markup and markdown amounts. Which concept did you find more challenging to understand, and why?
3. A sporting goods store uses a markup of 87.5% for baseball bats. What is the price the store should display for a baseball bat with an original cost of $40?
A. Use words to complete the equation you should use to find the amount of the markup.
____ = percent × ____

B. Because the store marks up the original cost, the price will (decrease /increase). The percent change is ____%.
C. Write an equation that gives the retail price y of a bat with an original cost of x.
y = ___ x + ___ x = ___ x
D. To find the price that the store should display, substitute ____ for x in the equation in Part C. The store should display a price of $ ___
Answer:
A sporting goods store uses a markup of 87.5% for baseball bats
40 × (1 + 87.5%)
40 × (1 + 875/100)
40 × (1+ 0.875)
40 × (1.875) = 75
Check Understanding
Question 1.
This weekend the hardware store is having a blowout sale, where everything is discounted 40%. A weed eater originally sells for $145. How much will the weed eater cost during the blowout sale?
______________
Answer:
Given,
This weekend the hardware store is having a blowout sale, where everything is discounted 40%.
A weed eater originally sells for $145.
145 × (1 – 40%)
145 × (1 – 40/100)
145 × (1 – 0.4)
145 × 0.6 = 87
The weed eater cost $87 during the blowout sale.
Question 2.
A grocery store buys organic apples for $0.75 per apple. The grocery store marks up the cost of each apple by 18%. To the nearest cent, how much will one organic apple cost at the grocery store?
______________
Answer:
Given,
A grocery store buys organic apples for $0.75 per apple.
The grocery store marks up the cost of each apple by 18%.
0.75 × (1 + 18%)
0.75 × (1 + 18/100)
0.75 × (1 + 0.18)
0.75 × (1.18) = 0.89
Thus the organic apple costs $0.89 at the grocery store.
Question 3.
A hailstorm caused damage at a car lot. A compact car usually sells for $27,500, but the damaged cars are discounted to $17,875. What was the percent discount on a damaged compact car?
______________
Answer:
Given,
A hailstorm caused damage at a car lot.
A compact car usually sells for $27,500, but the damaged cars are discounted to $17,875
Percent Discount is 100% – (17875/27500) × 100%
100% – (0.65) × 100%
100% – 65% = 35%
Thus the percent discount on a damaged compact car is 35%
Question 4.
A store is selling all toaster ovens at 15% off. Write an equation in the form y = kx to represent the sale price y in dollars of a toaster with an original retail price of x dollars. Then find the amount Jill paid for a toaster with an original retail price of $40.
______________
Answer:
A store is selling all toaster ovens at 15% off.
Original retail price = $40
40 × (1 – 15%)
40 × (1 – 15/100)
40 × (1 – 0.15)
40 × 0.85 = $34
On Your Own
Question 5.
A hobby store marks up remote-controlled cars 20%. The original price was $35. What is the retail price to purchase a remote-controlled car at the hobby store?
______________
Answer:
A hobby store marks up remote-controlled cars 20%.
The original price was $35.
Retail price = 35 × 20%
35 × 20/100
35 × 0.2 = $7
Therefore the retail price to purchase a remote-controlled car at the hobby store is $7.
Question 6.
Organic hot dogs at the grocery store cost $2.00 each. At a major league baseball game, an organic hot dog costs $6.50. By what percent does the baseball field mark up its organic hot dogs?
______________
Answer:
Given,
Organic hot dogs at the grocery store cost $2.00 each.
At a major league baseball game, an organic hot dog costs $6.50.
$6.50 – $2 = $4.5
Question 7.
The Bakers want to sell their house for $145,500. After 2 months, the Bakers decided to mark down the price of their house 8% to sell more quickly. How much are the Bakers selling their house for now?
______________
Answer:
Given,
The Bakers want to sell their house for $145,500.
After 2 months, the Bakers decided to mark down the price of their house 8% to sell more quickly.
145500 × (1 – 8%)
145500 × (1 – 0.08)
145500 × (0.92) = 133860
Question 8.
Shelly’s Boutique had a Labor Day sale featuring 25% off any item. Tammy wanted to buy a blouse that originally sold for $21.99. To the nearest cent, how much will it cost her, before tax, to buy the blouse during the sale?
______________
Answer:
Given,
Shelly’s Boutique had a Labor Day sale featuring 25% off any item.
Tammy wanted to buy a blouse that originally sold for $21.99.
21.99 × (1 – 25%)
21.99 × (1 – 25/100)
21.99 × (1 – 0.25)
21.99 × 0.75 = $16.49
Therefore Shelly paid $16.49 for the shirt.
Question 9.
The pair of shoes shown had a sale price of $76.50. What was the retail price?
______________

Answer:
The pair of shoes shown had a sale price of $76.50.
Discount = 10%
76.50(1 – 10%)
76.50 (1 – 0.1)
76.5 × 0.9 = $68.85
Thus the retail price is $68.85
Question 10.
Model with Mathematics A convenience store sells prepaid mobile phones. It purchases them for $12 each and uses a markup rate of 250%.
A. What is the markup rate in decimal form? _____
Answer: Markup rate = 250%
The markup rate in decimal form is 250/100 = 2.5
B. The markup rate is the constant of proportionality in the equation y = kx. Write an equation that can be used to find the markup on the cost x of a phone.
______________
Answer:
y = kx
The markup rate is k
Markup rate is 2.5
So, the equation will be y = 2.5x
C. Using the equation, calculate the markup amount.
______________
Answer:
12 × (1 + 2.5)
12 × 3.5 = $42
D. What is the retail price of a phone?
______________
Answer: The retail price of a phone is $42.
Next week the store is going to reduce the price to $31.50.
E. Calculate what percent the sale price is of the retail price. Show your work.
______________
Answer:
F. Think of the retail price of the phone as 100%. How does the sale price compare to the retail price? What does this tell you about the markdown rate?
______________
Answer:
G. What is an equation in the form y = kx that relates the sale price to the retail price x?
______________
Answer:
For Problems 11-13, find the new price for the markup, markdown, or discount given. Round to the nearest cent if necessary.
Question 11.
$12.99 marked down 25%
______________
Answer:
12.99 × (1 – 25%)
12.99 × (1 – 25/100)
12.99 × (1 – 0.25)
12.99 × 0.75 = 9.74
Thus the markdown price is $9.74
Question 12.
$3.00 marked up 72%
______________
Answer:
3 × (1 + 72%)
3 × (1 + 72/100)
3 × (1 + 0.72)
3 × 1.72 = 5.16
The markup price is $5.16
Question 13.
$125.49 discounted 30%
______________
Answer:
125.49 × (100% – 30%)
125.49 × 70%
125.49 × 0.7 = $87.84
Question 14.
The thrift store is selling their old DVDs. When the DVDs first came out, they sold for $19. They have now been marked down by 75%. What is the discounted price of a DVD?

Answer:
Given,
The thrift store is selling their old DVDs. When the DVDs first came out, they sold for $19.
They have now been marked down by 75%.
19 × (1 – 75%)
19 × (1 – 0.75)
19 × 0.25 = $4.75
Thus the discounted price of a DVD is $4.75
Question 15.
A manufacturer makes handwoven scarves for $10 and them to retail boutiques around the country. The boutiques sell the scarves for $25. What percent markup do the boutiques charge their customers?
Answer:
Given,
A manufacturer makes handwoven scarves for $10 and them to retail boutiques around the country.
The boutiques sell the scarves for $25.
(25 – 10)/10
15/10 = 1.5
1.5 × 100/100 = 150%
Thus 150 percent markup the boutiques charge their customers.
Question 16.
Model with Mathematics Melissa makes apple pies and sells them with a markup of 78%.
A. Write an equation representing the retail price y of Melissa’s apple pies in terms of the original cost x.
______________
Answer:
Original cost of apple pie = x
The markup percentage = 78%
The retail price of the apple pie = y
78% of x = 78/100 × x = 0.78x
Thus the markup price of apple pie = 0.78x
Total retail price = original price + markup price
= x + 0.78x = 1.78x
y = 1.78x
B. If it costs Melissa $8.20 to make a pie, how much should she charge for a pie? Round your answer to the nearest cent if necessary.
______________
Answer:
If it costs Melissa $8.20
y = 1.78x
x = 8.20
we know that
y = 1.78x
y = 1.78 × 8.2
y = $14.596
Question 17.
Reason A local jewelry store sells class rings, which it purchases for $60 each. The store engraves a name and date on the ring, and sells it using a markup rate of 340%.
A. What is the markup rate in decimal form? _____
Answer:
Markup rate = 340%
340/100 = 3.4
B. The markup rate is the constant of proportionality in the equation y = kx. Write an equation that can be used to find the amount of markup on the cost x of a ring.
_______________________
Answer:
y = 3.4x
C. Use the equation to find the markup amount by substituting the cost of a ring for x.
_______________________
Answer:
y = 340/100 × x
y = 17/5 x
5y = 17x
D. Calculate the retail price of a ring. Show your work.
_______________________
Answer:
60 × 3.4 = 204
During graduation week, the store is going to reduce the price to $184.80.
E. Calculate what percent the sale price is of the retail price. Show your work.
_______________________
Answer:
F. Think of the retail price of the ring as 100%. How does the sale price compare to the retail price? What does this tell you about the markdown rate?
_______________________
Answer:
G. What is an equation in the form y = kx that relates the sale price to the retail price x?
_______________________
Answer:
Question 18.
All of last year’s car models were marked down 40%. Tracy wants to buy a car on sale for $18,000. What was the retail price of the car?
_______________________
Answer:
Given,
All of last year’s car models were marked down 40%.
Tracy wants to buy a car on sale for $18,000.
18000 × 40%
18000 × 40/100
18000 × 0.4 = 7200
18,000 + 7200 = 25,200
Thus the retail price of the car is $25,200.
For Problems 19-22, find the new price after the markup, markdown, or discount given. Round to the nearest cent if necessary.
Question 19.
$100 marked down 65%
_______________________
Answer:
100(1 – 65%)
100 × (1 – 65/100)
100 × (0.35) = $35
Percent = 35 × 100/100 = 3500%
Question 20.
$78 discounted 12%
_______________________
Answer:
78 × (1 – 12%)
78 × (1 – 0.12)
78 × 0.88 = $68.64
Question 21.
$145 marked up 175%
_______________________
Answer:
145 × (1 + 175%)
145 × (1 + 1.75)
145 × (2.75) = 398.75
Percent = 398.75 × 100/100 = 39875%
Question 22.
$34,589 discounted 8%
_______________________
Answer:
$34,589 discounted 8%
34589 × (1 – 8%)
34589 (1 – 8/100)
34589 (1 – 0.08)
34589 (0.92) = 31821.88
Lesson 2.2 More Practice/Homework
Question 1.
A local nonprofit organization is selling popcorn to raise money for hurricane relief. The organization paid $4 per bag for the popcorn and sold it for $5 per bag. What was the percent markup on each bag of popcorn?
Answer:
Given,
A local nonprofit organization is selling popcorn to raise money for hurricane relief.
The organization paid $4 per bag for the popcorn and sold it for $5 per bag.
Mark up = 5 – 4 = 1
percent of mark up – 5 – 4 = 1
1/4 × 100 = 25%
Question 2.
The high school decided to buy new uniforms for the girls’ and boys’ basketball teams. They plan to buy 35 uniforms with a total cost of $1,235. The store offers discounts based on the number of items the school buys, as shown. What will the discounted price be for the high school?

Answer:
Given,
The high school decided to buy new uniforms for the girls’ and boys’ basketball teams.
They plan to buy 35 uniforms with a total cost of $1,235.
35 is in between 25 and 49
So, the discounted price for the high school is 15%
1235 × (1 – 15%) = 1049.75
Question 3.
Open Ended Describe a real-life situation involving markup, markdown, or discount that the equation y = x + 0.4x could represent.
Answer:
y = x + 0.4x (markup)
The retail price is y in dollars for an item with the original cost x and a markup of 40%.
For Problems 4-8, find the new price for the markup, markdown, or discount given. Round to the nearest cent if necessary.
Question 4.
$6.25 marked up 25%
______________
Answer:
$6.25 marked up 25%
6.25 (1 + 25%)
6.25(1 + 25/100)
6.25 (1 + 0.25)
6.25(1.25) = 7.8125
Question 5.
$13.50 discounted 75%
______________
Answer:
$13.50 discounted 75%
13.50 × 75%
13.50 × 0.75 = $10.12
13.50 – 10.12 = $3.38
Question 6.
$112 marked down 40%
______________
Answer:
112 × (1 – 40%)
112 (1 – 40/100)
112 (1 – 0.4)
112 × 0.6 = $67.2
Question 7.
$220 marked up 60%
______________
Answer:
$220 marked up 60%
220/100 = 2.2
2.2 × 60 = 132
132 + 220 = 352
Thus the revenue is $352 and profit is $132.
Question 8.
$5,250 marked down 15%
______________
Answer:
$5,250 marked down 15%
Marked down 15% means the new price would be 85% of the original price ( 100%-15% – 85%)
5250 × 0.85 = 4462.50
Thus the new price is $4462.50
Test Prep
Question 9.
Nate just started working at a clothing store. He receives a 40% discount on any item once a month. This month Nate decided to buy a jacket that has a retail price of $74.99. How much did Nate pay for his jacket?
A. $29.99
B. $34.99
C. $44.99
D. $104.99
Answer:
Given,
Nate just started working at a clothing store.
He receives a 40% discount on any item once a month.
This month Nate decided to buy a jacket that has a retail price of $74.99.
74.99 × (1 – 40%)
74.99 × (1 – 40/100)
74.99 × (1 – 0.4)
74.99 × 0.6 = 44.99
Thus option C is the correct answer.
Question 10.
Cup o’ Coffee buys its coffee for $1.25 a cup. The coffee shop then sells each cup for $3.75. What is the percent markup for a cup of coffee?
A. 300%
B. 200%
C. 66.6%
D. 33.3%
Answer:
Given,
Coffee buys its coffee for $1.25 a cup.
The coffee shop then sells each cup for $3.75.
(3.75 – 1.25) ÷ 1.25
2.5 ÷ 1.25 = 2
2 × 100/100 = 200%
Thus option B is the correct answer.
Question 11.
Write an equation that represents a discount of 18% on a retail price of $55. Let p represent the new price.
_______________________
Answer:
Discount = 18%
Retail price = $55
55(1 – 18%)
55(1 – 18/100)
55(1 – 0.18)
55 × 0.82 = 45.1
55(1 – 18%) = p
Thus the new price is $45.1
Question 12.
Brooke needs a new computer. On Friday, the computer was $200. On Saturday, the price of the computer was $149. Determine if there was a markup or markdown and by what percent.
A. markup; 25.5%
B. markup; 34.5% .
C. markdown; 25.5%
D. markdown; 34.5%
Answer: C. markdown; 25.5%
Explanation:
The rate of price change = (current price – original price)/ original price × 100%
= (149-200)/200 × 100%
= -25.5% <0
Therefore markdown 25.5%
Option C is the correct answer.
Spiral Review
Question 13.
Determine whether the cost of grapes is proportional to the number of pounds. Explain.

Answer:
The ratio of cost of grapes to the number of pounds = 3:1
6:2 = 3:1
9:3 = 3:1
12:4 = 3:1
Hence the cost of grapes is proportional to the number of pounds.
Question 14.
Find the range of allowable values based on an expected mass of 250 grams for which values are allowed to vary by 5%.
_______________________
Answer:
250 × 5% = 250 × 5/100 = 25 × 1/2 = 12.5 grams
250 – 12.5 = 237.5 grams
250 + 12.5 = 262.5 grams