We included HMH Into Math Grade 7 Answer Key PDF Module 2 Lesson 3 Taxes and Gratuities to make students experts in learning maths.
HMH Into Math Grade 7 Module 2 Lesson 3 Answer Key Taxes and Gratuities
I Can use equations to represent the total cost of items with taxes and gratuities.
Step It Out
1. Jeremy got a haircut and paid 15% as a tip.

A. What percent of the cost did Jeremy pay the barber, including the tip?
_________________
Answer:
Given that,
The cost of hair cut = $15
Jeremy paid a tip = 15%
15% of $15 is $2.25
Jeremy paid to the barber including tip is $15 + $2.25
= $17.25
Therefore Jeremy paid the barber including a tip $17.25.
B. What is the cost of the haircut?
_________________
Answer: The cost of hair cut is $15.
C. Calculate the total cost of the haircut, including the tip. Show your work.
_________________
Answer:
The cost of hair cut = $15
Jeremy paid a tip = 15%
15% of $15 is $2.25
Jeremy paid to the barber including tip is $15 + $2.25
= $17.25
The total cost of hair cut including tip is $17.25
D. If you only wanted to know the tip amount, how would you change the process you used in Part C to calculate the total cost?
_________________
Answer:
If you only want tip. Calculate the percentage of tip in the total money. Then you get the tip money.
The total money is $15.
The tip percentage is 15%
15% of $15 is $2.25
The total money is $15 + $2.25 = $17.25.
Jeremy also bought a hair-care product priced at $13. The sales tax rate in his city is 7%.
E. Calculate the amount of tax. Show your work.
_________________
Answer:
The cost of the hair care product is $13.
The sales tax in the city is 7%
7% in the $13 is $0.91.
The tax amount is $0.91.
F. What is the total cost of the hair-care product plus tax?
_________________
Answer:
The cost of the hair care product is $13.
The sales tax in the city is 7%
7% in the $13 is $0.91.
The tax amount is $0.91.
The total cost of hair care plus tax is $13 + $0.91 = $13.91
G. How else could you find the total cost, including the tax?
_________________
Answer:
Yes, we can find the total cost including the tax.
The cost of the hair care product is $13.
The sales tax in the city is 7%.
7% in the $13 is $0.91.
The total cost including tax is $13.91.
Connect to Vocabulary
A gratuity is a percent that is given or paid in addition to the price of a service. It is also referred to as a tip.
Connect to Vocabulary
Sales tax is a percent that is added to the price of goods or services.
Turn and Talk How could you use fractions instead of decimals to calculate the amount of tax in Part E? Do you prefer to use fractions or decimals to compute taxes? Why?
2. Kelsey and Jamal went to lunch on Saturday. Their lunch cost $17.60, they gave the waiter a 15% gratuity on the amount before tax, and they were charged a 5% tax rate on the amount before gratuity. What was the total cost of the lunch?
A. Write an equation ¡n the form y = kx to find the amount of the gratuity y in dollars on an amount of x dollars. Then find the gratuity on Kelsey and Jamal’s bill.
y = ___x
y = ___ ∙ ____ = ___ The gratuity was $____.
Answer:
Given that,
The cost of lunch is $17.60.
Gratuity before tax is 15%.
The tax is 5%.
y = Kx
y = 15% x $17.60
y = $2.64
The gratuity was $2.64.
B. Write an equation in the form y = kx to find the tax y in dollars on an amount of x dollars. Then find the tax on Kelsey and Jamal’s bill.
y = ____x
y = ____ ∙ ____ = ____ The tax was $____
Answer:
Given that,
The cost of lunch is $17.60.
Gratuity before tax is 15%.
The tax is 5%.
y = Kx
y = 5% x $17.60
y = $0.88
The tax was $0.88.
C. Find the total cost of the lunch.
$17.60 + $____ + $____ = $____
Answer:
The cost of lunch is $17.60.
The gratuity was $2.64.
The tax was $0.88.
The total cost of the lunch is $17.60 + $2.64 + $ 0.88 = $21.12
Turn and Talk Round up the cost and explain how to use mental math to calculate a tip. Round the tip to the nearest dollar.
3. Nolan buys office supplies for his home business. Nolan paid a total of $210, which included a sales tax rate of 5%. What was the cost of the supplies before tax was added?
A. Write an equation for the total cost of the supplies, $210, in terms of the original cost x of supplies before tax. Then simplify.

___ = x + ___x
___ = ___x
B. Solve the equation to find x, the original cost of the supplies before tax.
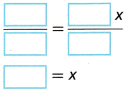
The total cost without the sales tax was $____.
C. Does your answer seem reasonable? Explain.
____________________
____________________
Answer:
Given,
Nolan buys office supplies for his home business.
Nolan paid a total of $210, which included a sales tax rate of 5%.
210 ÷ (1 + 5%)
210 ÷ (1 + 5/100)
210 ÷ (1 + 0.05)
210 ÷ 1.05 = 200
4. Miriam buys the chair shown. The tax rate is 7.5%. How much was the tax on the chair?

A. Write an equation in the form y = kx to find the amount y in dollars of the tax on an amount of x dollars. Then find the amount of tax on Miriam’s chair. Round to the nearest cent if necessary.
y = ___x
y = ____ ∙ ____ = ____
The tax was $____
Answer:
Given that,
The cost of the chair is $579.
The tax is 7.5%
The equation is y = Kx
y = 7.5%x
y = 7.5% x $579 = $43.425
The tax was $43.425
B. How do you know your answer is reasonable?
____________________
____________________
Answer: Yes, the answer is reasonable. Because the percentage of $579 is $43.425
C. Miriam pays a service to deliver the chair to her house. Her bill is $24.75, and she tips the driver 20%. What is the total expense for the delivery?
y = x + __x
y = ___x
y = ___ ∙ 24.75 = ___
The total expense is $____.
Answer:
Given that,
The cost of the bill is $24.75.
The tip of the driver is 20%
The equation is y = Kx
y = 20%x
y = 20% x $24.75.
y = $4.95
The total expense is $ 24.75 + $4.95 = $29.7
Check Understanding
Question 1.
Ella buys a computer for $785. Her local tax rate is 7%. How much does Ella pay for the computer, including tax?
Answer:
Given,
Ella buys a computer for $785. Her local tax rate is 7%.
785 × (1 + 7%)
785 × (1 + 7/100)
785 × (1 + 0.07)
785 × 1.07 = 839.95
Thus Ella pays $839.95 for the computer including tax.
Question 2.
Kim works as a Di and earns $1,250 to play music for 6 hours at a wedding reception. At the end of the night, she gets an 18% tip. How much in total did she earn?
Answer:
Given,
Kim works as a Di and earns $1,250 to play music for 6 hours at a wedding reception.
At the end of the night, she gets an 18% tip.
1250 × 18%
1250 × 18/100 = 225
1250 + 225 = 1475
Thus she earned $1475 in all.
Question 3.
Adrian shops for school clothes and spends a total of $93.42. If the local tax rate is 8%, how much was the cost without tax?
Answer:
Given,
Adrian shops for school clothes and spends a total of $93.42.
Tax rate = 18%
93.42 ÷ (1 + 8%)
93.42 ÷ (1 + 0.08)
93.42 ÷ 1.08 = 86.5
Thus the cost without tax is $86.50
On Your Own
Question 4.
The amount that a charter boat captain charges a group to go deep-sea fishing is shown. If the group tips the captain 17%, what is the total amount that the captain receives for the fishing trip?

Answer:
Given,
The amount that a charter boat captain charges a group to go deep-sea fishing is shown.
Tax rate = 17%
Cost of full day trips = $850
= 850 × (1 + 17%)
850 × (1 + 17/100)
850 × (1 + 0.17) = $994.50
Question 5.
The school secretary orders a new printer and pays $310.30 after tax. The tax rate is 7%. What was the original price of the printer?
______________
Answer:
Given,
The school secretary orders a new printer and pays $310.30 after tax.
The tax rate is 7%.
310.3 ÷ (1 + 7%)
310.30 ÷ (1 + 0.07)
310.3 ÷ (1.07) = 290
Thus the original price of the printer is $290.
For Problems 6 and 7, find the total amount given the original price and tax rate. Round to the nearest cent if necessary.
Question 6.
$15.25, 7%
______________
Answer:
$15.25, 7%
15.25 (1 + 7%)
15.25(1 + 0.07)
15.25(1.07) = $16.32
Question 7.
$31.69, 6%
______________
Answer:
$31.69, 6%
31.69 (1 + 6%)
31.69(1 + 0.06)
31.69(1.06) = $33.59
Question 8.
Miguel buys a car for $14,999. The tax rate is 6%. What is the total purchase price of the car?
______________
Answer:
Given,
Miguel buys a car for $14,999.
The tax rate is 6%.
14999(1 + 6%)
14,999(1 + 0.06)
14,999(1.06) = $15898.94
Question 9.
The music boosters have their year-end banquet at a hotel that charges $750. The president of the boosters tips the banquet team 20%. What is the total amount spent?
Answer:
Given,
The music boosters have their year-end banquet at a hotel that charges $750.
The president of the boosters tips the banquet team 20%.
750 (1 + 20%)
750 (1 + 20/100)
750(1 + 0.2)
750 × 1.2 = 900
The total amount spent is $900.
Question 10.
Model with Mathematics A family used a professional decorator to help furnish their new home. The decorator selected $1,580 worth of furnishings. The family paid for the furnishings, plus 4.5% tax on the purchases. The decorator’s fee was 12% of the purchases, not including the tax.
A. Write an equation in the form of y = kx to represent the decorator’s fee. Then use the equation to calculate the amount of that fee.
____________________
Answer:
Given,
The decorator selected $1,580 worth of furnishings.
The family paid for the furnishings, plus 4.5% tax on the purchases.
The decorator’s fee was 12% of the purchases.
Tax = 4.5% × 1580 = 0.045 × 1580 = $71.10
Amount paid = 1580 + 71.10 = 1651.10
B. Write an equation in the form of y = kx to represent the tax. Then use the equation to calculate the amount of tax.
____________________
Answer:
Since the decorator’s fee was 12% of the purchases. This will then be calculated as:
y = kx
where,
y = decorators fee
k = percentage of decorators fee on purchases
x = amount paid
y = 12% × $1651.10
= 0.12 × $1651.10
= $198.132
C. What is the total cost that the family paid? Show your work.
____________________
Answer: The total cost that the family paid is $1651.10
For Problems 11 and 12, find the total amount given the original price and tip rate. Round to the nearest cent if necessary.
Question 11.
$22.22, 10%
____________________
Answer:
Total amount = $22.22
Tip rate = 10%
22.22 ÷ (1 + 10%)
22.22 ÷ (1 + 10/100)
22.22 ÷ (1 + 0.1)
22.22 ÷ (1.1) = $20.2
Thus the original price is $20.2
Question 12.
$41.32, 15%
____________________
Answer:
Total amount = $41.32
Tip rate = 15%
41.32 ÷ (1 + 15%)
41.32 ÷ (1 + 15/100)
41.32 ÷ (1 + 0.15)
41.32 ÷ (1.15) = $35.93
Thus the original price is $35.93
Question 13.
A group of friends receives a dinner bill of $287.50 at a restaurant. The bill includes a 15% tip for the server. How much was the bill before the tip was added? Explain how you found your answer.
____________________
Answer:
Given,
A group of friends receives a dinner bill of $287.50 at a restaurant.
The bill includes a 15% tip for the server.
287.50 ÷ (1 + 15%)
287.50 ÷ (1 + 15/100)
287.50 ÷ (1 + 0.15)
287.50 ÷ (1.15) = $250
For Problems 14 and 15, find the original price given the total amount and tip rate.
Question 14.
$51.84, 20%
____________________
Answer:
Total amount = $51.84,
Tip rate = 20%
51.84 ÷ (1 + 14%)
51.84 ÷ (1 + 14/100)
51.84 ÷ (1 + 0.14)
51.84 ÷ (1.14) = $45.47
Thus the original price is $45.47
Question 15.
$38.35, 18%
____________________
Answer:
Total amount = $38.32
Tip rate = 18%
38.32 ÷ (1 + 18%)
38.32 ÷ (1 + 18/100)
38.32 ÷ (1 + 0.18)
38.32 ÷ (1.18) = $32.47
Thus the original price is $32.47
Question 16.
Jayme buys the painting shown for his apartment. The tax rate is 6.5%. How much did Jayme spend after tax? Round to the nearest cent if necessary.
____________________
Answer:
Given,
Jayme buys the painting shown for his apartment.
The tax rate is 6.5%.
179.99 × (1 – 6.5%) = $168.30
Thus Jayme spends $168.3 after tax.
Question 17.
A business traveler buys a round-trip plane ticket for $629. The tax rate is 7.5%. How much was the cost after tax? Round to the nearest cent if necessary.
____________________
Answer:
Given,
A business traveler buys a round-trip plane ticket for $629.
The tax rate is 7.5%.
629 × (1 – 7.5%)
629 × 0.925 = 581.825
= 581.83

For Problems 18 and 19, find the tax amount given the original price and tax rate. Round to the nearest cent if necessary.
Question 18.
$58.73, 6.5%
____________________
Answer:
Original price = $58.73
Tax rate = 6.5%
58.73 × 6.5%
58.73 × 6.5/100 = 3.817 ≈ 3.82
Question 19.
$73.81, 7.5%
____________________
Answer:
Original price = $73.81
Tax rate = 7.5%
73.81 × 7.5%
73.81 × 7.5/100 = $5.53
Question 20.
Three coworkers buy a baby shower gift for $60. The local tax rate is 6%. How much was the tax?
____________________
Answer:
Given,
Three coworkers buy a baby shower gift for $60.
The local tax rate is 6%.
60 × 6%
60 × 6/100 = 360/100 = 3.6
Question 21.
Devansh buys a house for $189,900. The tax rate is 7.5%. How much was the tax on the home?
____________________
Answer:
Given,
Devansh buys a house for $189,900. The tax rate is 7.5%.
189900 × 7.5%
189900 × 7.5/100 = 14242.50
$14242.50 was the tax on the home.
Question 22.
Model with Mathematics The cost x of the Sennet family’s meal at a restaurant is $172.65, and they tip 20%. Write and use an equation to find the total cost y of the dinner.
____________________
Answer:
Given,
The cost x of the Sennet family’s meal at a restaurant is $172.65, and they tip 20%.
172.65 × (1 + 20%)
172.65 × (1 + 0.2)
172.65 × 1.2 = $207.18
Question 23.
Mrs. Carissi purchased a new smartphone. The cost of the phone was $675 and the local tax rate is 6.2%.
A. Write an equation in the form y = kx to represent the amount of tax. Use the equation to calculate the amount of the tax. Round to the hundredths place if necessary.
y = ___x
y = ____ ∙ 675 = ___
The tax was ____
Answer:
Given that,
The cost of the phone was $675.
The tax rate is 6.2%.
y = 6.2%x
y = 6.2% x 675 = 41.85
The tax was 41.85.
B. Reason How do you know your answer is reasonable?
Answer: Yes, the answer is reasonable. Because the percentage of 675 is 41.85.
Mrs. Carissi hired a service to enter all her friends’ numbers into her phone and
to set up some apps. The service charged $22. and she added a tip of 15%.
C. Write an equation in the form y = kx, where k is the total rate in the form of a decimal. Use the equation to calculate the total expense of setting up the phone. Round to the hundredths place if necessary.
y = x + ___x
y = ___x
y = ___ ∙ 22 = $___
Answer:
The service charged $22.
She added a tip of 15%.
The equation is y = kx
y = 15%x.
y = 15% x $22.
y = $3.3
D. How do you know your answer is reasonable?
_________________
Answer: Yes, our answer is reasonable because the 15 % of $22 is $3.3.
For Problems 24 and 25, write an equation for the total amount y after the given rate of increase is added to the original amount x.
Question 24.
20%
______________
Answer:
y = x(1 + 20%)
y = x(1 + 20/100)
y = x(1 + 0.2)
y = 1.2x
Question 25.
8.5%
______________
Answer:
y = x(1 + 8.5%)
y = x(1 + 8.5/100)
y = x(1 + 0.085)
y = 1.085x
For Problems 26 and 27, find the original price given each total amount and rate of increase. Round tó the nearest cent if necessary.
Question 26.
$83.82, 10%
______________
Answer:
$83.82, 10%
83.82 ÷ (1 + 10%)
83.82 ÷ (1 + 0.1)
8382 ÷ 1.1 = 76.2
So, the original price is $76.20
Question 27.
$93.72, 6%
______________
Answer:
$93.72, 6%
93.72 ÷ (1 + 6%)
93.72 ÷ (1 + 0.06)
93.72 ÷ 1.06 = 88.41
So, the original price is $88.41
Lesson 2.3 More Practice/Homework
Question 1.
Beau buys a skateboard with a price tag of $82.50. The tax rate is 8%. How much does he pay, including tax? ________
Answer:
Given,
Beau buys a skateboard with a price tag of $82.50. The tax rate is 8%.
82.5 × (8% + 1)
82.5 (8/100 + 1)
82.5 (0.08 + 1)
82.5 × 1.08 = 89.1
Thus he pays $89.10 including the tax.
Question 2.
Professor Burger orders flowers to be delivered to his mother. The flowers cost $59.95, not including tax. If there is a 6% sales tax, what is the total cost of the flowers to the nearest cent?

Answer:
Given,
Professor Burger orders flowers to be delivered to his mother.
The flowers cost $59.95, not including tax.
59.95 × (6% + 1)
59.95 × (6/100 + 1)
59.95 × (0.06 + 1)
59.95 × 1.06 = 63.55
The total cost of the flowers is $63.55
Question 3.
Monty takes a cab to work and pays a fare of $12.75. He tips the driver 20% and the tax rate is 8%. How much does he spend on the trip?
Answer:
Given,
Monty takes a cab to work and pays a fare of $12.75. He tips the driver 20% and the tax rate is 8%.
12.75 × (1 + 8% + 20%)
12.75 × (1 + 28%)
12.75 × (1 + 0.28)
12.75 × 1.28 = 16.32
Thus he spends $16.32 on the trip.
Question 4.
Mary Jo takes her son to get a haircut at the barbershop. The total cost of the haircut ¡s $12.60, including a 20% tip. How much was the haircut before the tip?
Answer:
Given,
Mary Jo takes her son to get a haircut at the barbershop.
The total cost of the haircut is $12.60, including a 20% tip.
x × (1 + 20%) = $12.60
x(1 + 0.2) = 12.60
1.2x = 12.60
x = 12.60 ÷ 1.2
x = 10.50
Therefore the cost of a haircut before the tip is $10.50
Question 5.
Derek and Jeannine buy a car for a total price, including tax, of $19,795. The price of the car was $18,500. What is the tax rate?
Answer:
Given,
Derek and Jeannine buy a car for a total price, including tax, of $19,795.
The price of the car was $18,500.
19,795 – 18,500 = 1295
Rate = 1295/18500 × 100%
Rate = 0.07 × 100% = 7%
Attend to Precision For Problems 6 and 7, find the total amount given the original price and tax or tip rate. Round to the nearest cent if necessary.
Question 6.
$123.28, 7.5%
________
Answer:
Original price = $123.28
tax = 7.5%
= 123.28 × 7.5%
= 123.28 × 7.5/100
= $9.246
Total amount = $123.28 + $9.25
= $132.53
Question 7.
$156.67, 6%
________
Answer:
Original price = $156.67
Tax = 6%
= 156.67 × 6%
= 156.67 × 6/100
= $9.40
Total amount = $156.67 + $9.40
= $166.07
For Problems 8 and 9, find the total amount given the original price, tax rate, and tip rate. Round to the nearest hundredth if necessary.
Question 8.
$90.34, 3.5%, 20%
________
Answer:
$90.34, 3.5%, 20%
The original price = $90.34
Tax rate = 90.34 × 20% = 90.34 × 20/100 = 18.068
The tip rate = 90.34 × 3.5% = 90.34 × 3.5/100 = 3.1619
Question 9.
$101.33, 6.7%, 18%
________
Answer:
$101.33, 6.7%, 18%
The original price = $101.33
Tax rate = 101.33 × 18% = 101.33 × 18/100 = $18.2394
The tip rate = 101.33 × 6.7% = 101.33 × 6.7/100 = $6.78911
For Problems 10 and 11, find the original price given the total amount and tax or tip rate.
Question 10.
$128,500, 5.5%
Answer:
Total price = $128,500
Tax rate = 5.5%
Original price = total price – tax rate
= 128500 × (1 – 5.5%)
= 128500 × 94.5/100 = 121432.50
Hence the original price is $121432.50
Question 11.
$307.32, 20%
Answer:
Total price = $307.32
Tax rate = 20%
Original price = total price – tax rate
= 307.32 × (100 – 20%)
= 307.32 × 80/100 = $245.856
Hence the original price is $245.856
Test Prep
Question 12.
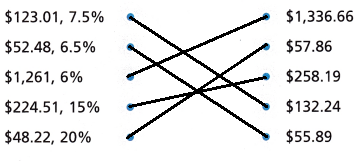
Match the amounts and tip or tax rates in the first column to the total costs in the second column.

Answer:
123.01 × (1 + 7.5%) = $132.24
52.48 × (1 + 6.5%) = 55.89
1261 × (1 + 6%) = 1336.66
224.51 × (1 + 15%) = 258.19
48.22 × (1 + 20%) = 57.86
Question 13.
Brett plays an acoustic guitar at an event for $500. At the end of the event, the sponsor tips him 20%. How much does Brett make at this event?
__________________
Answer:
Given,
Brett plays an acoustic guitar at an event for $500.
At the end of the event, the sponsor tips him 20%.
500 × 20%
500 × 20/100 = 100
Question 14.
Carmine buys a canoe priced at $478. He pays a total, including tax, of $509.07. What was the tax rate?
A. 6%
B. 6.5%
C. 7%
D. 7.5%
Answer:
Given,
Carmine buys a canoe priced at $478.
He pays a total, including tax, of $509.07.
(509.07 – 478) ÷ 478
31.07/478 = 0.065
0.065 × 100/100 = 6.5/100 = 6.5%
Thus option B is the correct answer.
Question 15.
Ana buys a toolbox, drill set, and socket set. She spends a total of $564.45 after tax, and the tax rate is 6%. What was the total price before tax?
A. $540.04
B. $537.50
C. $534.99
D. $532.50
Answer:
Given,
Ana buys a toolbox, drill set, and socket set.
She spends a total of $564.45 after tax, and the tax rate is 6%.
564.45 ÷ (1 + 6%)
564.45 ÷ (1 + 0.06)
564.45 ÷ (1.06)
564.45/1.06 = 532.5
Thus the total price before tax is $532.50
Option D is the correct answer.
Spiral Review
Question 16.
An 8-ounce cup of juice costs $1.20. A 12-ounce cup of the same juice costs $1.44. Can the relationship between cost and ounces of juice be described by a constant rate? Explain.
Answer:
Given,
An 8-ounce cup of juice costs $1.20.
A 12-ounce cup of the same juice costs $1.44.
1.2/8 = 0.15
1.44/12 = 0.12
0.15 ≠ 0.12
1.2/8 ≠ 1.44/12
Therefore the relationship between cost and ounces of juice can’t be described by a constant rate.
Question 17.
Last year, 320 students were members of Pine Hill Middle School clubs. This year, there was a 20% increase in memberships. How many students are members this year?
Answer:
Given,
Last year, 320 students were members of Pine Hill Middle School clubs.
This year, there was a 20% increase in memberships.
320 × (1 + 20%)
320 × (1 + 20/100)
320 × (1 + 0.2)
320 × 1.2 = 384
384 students are members this year.