We included HMH Into Math Grade 7 Answer Key PDF Module 15 Lesson 3 Use Theoretical Probability and Proportional Reasoning to Make Predictions to make students experts in learning maths.
HMH Into Math Grade 7 Module 15 Lesson 3 Answer Key Use Theoretical Probability and Proportional Reasoning to Make Predictions
I Can use theoretical probability to make predictions about real-world situations.
Step It Out
Question 1.
Sadie spins the spinner shown 80 times. Predict how many times she will spin a 2 or 3.
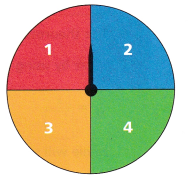
A. The theoretical probability of spinning a 2 or 3 is _________, or _________ %
Answer:
Given that,
Sadie spins the spinner 80 times.
She spins 2 of is
The theoretical probability of spinning a 2 or 3 is 40 or 80%.
B. Solve by using proportional reasoning.
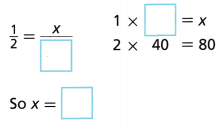
Sadie will spin a 2 or 3 about ____________ times.
Answer:
1/2 = x/40
1 × x = x
2 × 40 = 80
So, x = 40.
Sadie will spin 2 or 3 about 40 times.
C. Solve by multiplying the probability by the number of trials.
P(spinning 2 or 3) × number of trials
![]() % ×
% × ![]() =
= ![]()
Sadie will spin a 2 or 3 about ________ times.
Answer:
The probability of spinning 2 or 3 is 40.
The number of tries = 80
40% × 80 = 32.
Sadie will spin 2 or 3 about 32 times.
Question 2.
Bailey rolls a number cube 180 times. Predict how many times she will roll a 5 or 6.
A. The theoretical probability of rolling a 5 or 6 is ________, or ___________.
Answer:
Given that,
Bailey rolls a number cube = 180 times.
The theoretical probability of rolling a 5 or 6 is 60 or 180 times.
B. Solve by using proportional reasoning.
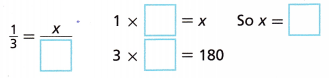
Bailey will roll a 5 or 6 about __________ times.
Answer:
1/3 = x/40
1 × x = x
3 × 60 = 180
So, x = 60
Bailey will roll a 5 or 6 about 60 times.
C. Solve by multiplying the probability by the number of trials.
P(spinning 5 or 6) × number of trials
![]() % ×
% × ![]() =
= ![]()
Bailey will roll a 2 or 3 about ___________ times.
Answer:
Given that,
The number of trials = 180
The probability of spinning 5 or 6 is 60
60% x 180 = 108
Bailey will roll a 2 or 3 about 108 times.
Question 3.
Jamie works at a dog shelter. The types, colors, and genders of dogs are shown. Predict how many times out of 90 Jamie will randomly pick a tan, male pug to walk. Assume an equal chance for her to select each dog.

A. Make a tree diagram or organized list to represent the sample space.
Answer:
B. The theoretical probability of selecting a tan, male pug is ____________.
Answer:
C. Solve by using proportional reasoning.
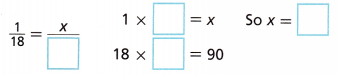
Jamie will select a tan, male pug about ___________ out of 90 times.
Answer:
D. Solve by multiplying the probability by the number of times she picks.
P(tan, male, pug) × number of times
![]() ×
× ![]() =
= ![]()
Jamie will select a tan, male pug about __________ out of 90 times.
Answer:
E. Predict how many times out of 90 Jamie will randomly select a tan pug or tan collie. Use the sample space to find the probability.
There are __________ tan pugs and tan collies in the sample space.
P(tan pug or tan collie) = 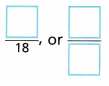
Solve by using proportional reasoning.
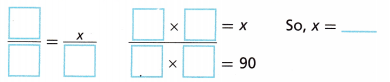
Jamie will select a tan pug or tan collie about _________ out of 90 times.
Answer:
Turn and Talk Describe an alternate solution method for Part E.
Answer:
Question 4.
Ezekiel randomly draws a card from the stack shown. Which is more likely: drawing a card that is NOT red or drawing a green card?
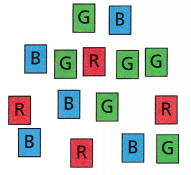
A. First find P(red). Then find P(not red).
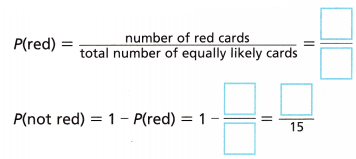
Answer:
Given that,
The number of red cards = 4.
The total number of cards = 15.
The formula for the probability of red = number of red cards/ total number of equally likely cards = 4/15.
The probability for not red = 1 – 4/15 = 11/15
B. Complete the inequality statement to compare P(not red) and P(green).

So drawing (not red / green) is more likely.
Answer:
The number of red cards = 6
The total number of cards = 15
The formula for the probability of red = number of red cards/ total number of equally likely cards = 6/15
The probability for not red = 1 – 4/15 = 11/15.
11/15 > 6/15
So, drawing green is more likely.
Question 5.
Isla is resetting her door code. The code is a 3-digit number made up of the digits O through 9. The digits can be repeated. Isla used a random number generator to select a code so all possible codes are equally likely. Would you predict that the door code 567 will be generated more than 5 out of 8,000 times?
A. First find the number of equally likely outcomes in the sample space.
Imagine drawing a tree diagram. There are 10 possible outcomes for the first digit, and each of those has 10 possible outcomes for the second digit, and each of those 10 more.
The sample space has 10 × 10 × 10 = ___________ equally likely outcomes.
Answer:
B. Find the probability of randomly generating the code 567, and use it to predict the number of times out of 8,000 you would expect code 567 to be generated.

I (would/would not) predict that the code 567 will be generated more than 5 out of 8,000 times.
Answer:
Check Understanding
Question 1.
A bag of marbles contains 5 red, 3 blue, and 12 yellow marbles. Predict the number of times Hazel will select a blue marble out of 500 trials.
Answer:
Given that,
The number of red marbles = 5
The number of blue marbles = 3
The number of yellow marbles = 12
The probability of the blue marble = number of blue marbles / total number of marbles = 3/20 = 0.15.
The blue marble out of 500 trials = 0.15 x 500 = 75 times.
Question 2.
Kai flips a coin and spins a 3-sector spinner labeled 1-3. Predict the number of times Kai will get the outcome (heads, 2) in 300 trials.
Answer:
Kai flips a coin and the outcome is headed then the probability of head = 1/2
Kai gets the outcome heads in 300 trials = 1/2 x 300 = 150 times.
Kai spins a 3-sector spinner get the outcome 2 is
The probability of 2 is = sector 2/number of sectors = 2/3
Kai gets an outcome 2 on the spinner is 2/3 x 300 = 200 times.
On Your Own
Question 3.
Construct Arguments Bryson selects a folder from a pile. The folder is blue. There are 8 blue folders, 9 yellow folders, and 3 orange folders left in the pile. He selects a second folder from the pile without looking. Is it likely that Bryson selects matching folders? Explain your reasoning.
Answer:
Model with Mathematics An eight-sided game piece has 8 congruent triangular faces. The faces are labeled 1-8. Nevaeh rolls the game piece 400 times. Use this information for Problems 4-7.

Question 4.
Write and solve a proportion to predict how many times the game piece will land on 7.
Answer:
Given that,
An eight-sided game piece has 8 congruent triangular faces.
Nevaeh rolls the game piece 400 times.
Probability of 7 = number of favourable outcomes/Total outcomes = 1/8
The probability of 7 for the 400 times = 1/8 x 400 = 50 times.
Question 5.
Write and solve a proportion to predict how many times the game piece will land on 3 or 5.
Answer:
Given that,
An eight-sided game piece has 8 congruent triangular faces.
Nevaeh rolls the game piece 400 times.
The game piece will land on 3 or 5. Then the number of outcomes is 2
Probability of 3 or 5 is = number of favorable outcomes/Total outcomes = 2/8
The probability of 3 or 5 for the 400 times = 2/8 x 400 = 100 times.
Question 6.
Write and evaluate an expression to predict how many times the game piece will land on an even number.
Answer:
An eight-sided game piece has 8 congruent triangular faces.
In those 8 congruent triangular faces, there are 4 even numbers. So, the number of outcomes is 4.
Nevaeh rolls the game piece 400 times.
The probability of a even number is = the number of favorable outcomes/Total outcomes = 4/8
The probability of 4 even numbers for the 400 times = 4/8 x 400 = 200 times.
Question 7.
Write and evaluate an expression to predict how many times the game piece will land on a number less than or equal to 3.
Answer:
Given that,
The game piece will land on a number less than or equal to 3 means the number of outcomes is 3.
Nevaeh rolls the game piece 400 times.
Probability of a number less than 3 or equal to 3 = number of favorable outcomes/Total outcomes = 4/8
The probability of a number less than 3 or equal to 3 for the 400 times = 3/8 x 400 = 150 times.
Liliana spins a spinner with equal-sized sections numbered 1 through 4. She spins the spinner a total of 300 times. Use this information for Problems 8-9.
Question 8.
Write and solve a proportion to predict the number of times Liliana can expect to spin a 3.
Answer:
Given that,
Liliana spins a spinner with 4 sections.
She spins the spinner a total of 300 times.
The number of times Liliana can expect to spin a 3 is
The number of outcomes to spin a 3 is 1
The probability of spin on 3 = number of favorable outcomes/ total number of outcomes = 1/4
The probability of spin on 3 for 300 times = 1/4 x 300 = 75 times.
Question 9.
Write and evaluate an expression to predict the number of times Liliana can expect to spin an even number.
Answer:
Given that,
In 4 sections there are 2 even numbers.
The number of outcomes is 2
The probability to spin on even numbers is = number of favorable outcomes/ total number of outcomes = 2/4
The probability of spin on even numbers for 300 times = 2/4 x 300 = 150 times.
Question 10.
Ezra is resetting the code on his safe. The code is a 3-digit number made up of the digits 0 through 5. The digits can be repeated. Ezra will randomly draw numbers from a hat to select a code, replacing the number after each draw. Is it likely that Ezra will randomly select the safe code 123 more than 10 times out of 4,320 random codes drawn from the hat? Solve using an expression. Explain your reasoning.

Answer:
Question 11.
Savannah is going to randomly select a block from a bag and return it to the bag 240 times. There are 3 colors (red, green, yellow) and two shapes (square and triangle). Explain how to find the sample space. Then predict how many times Savannah will select a red triangle. Solve using a proportion.
Answer:
Model with Mathematics Elliot rolls two number cubes 900 times. Their faces are labeled 1-6. Use this information for Problems 12-15.
Question 12.
Write and solve a proportion to predict the number of times Elliot can expect to roll a sum of 11.
Answer:
Given that,
Elliot rolls two number cubes 900 times.
1 die has 6 sides
2 dies = 6 x 6 = 36 sides.
To roll a sum of 11 the number of favorable outcomes is 2
The probability of sum of 11 = number of favourable outcomes/ total number of outcomes = 2/36 = 1/18
The probability of a sum of 11 for 300 times = 1/18 x 900 = 50 times.
Question 13.
Write and solve a proportion to predict the number of times Elliot can expect to roll two odd numbers.
Answer:
Question 14.
Write and evaluate an expression to predict the number of times Elliot can expect to roll one even number and one odd number.
Answer:
Question 15.
Write and evaluate an expression to predict the number of times Elliot can expect to roll the same number on both cubes.
Answer:
Question 16.
Penelope selects an earring from a jewelry box. The earring color is gold. The colors of the remaining earrings are: 11 gold, 16 silver, and 13 black. She randomly selects a second earring from the jewelry box. Is it likely that Penelope selects earrings of the same color? Explain your reasoning.
Answer:
Question 17.
Construct Arguments The security desk for an office building has visitor’s badges with codes consisting of one letter (A-Z) and 1 digit (0 through 9). A visitor can select a badge at random and badges are returned at the end of each day. Is it likely that the badge L7 is the first badge selected more than 5 times in 365 days? Explain your reasoning. (Hint: Imagine making a a rectangular array. There would be 26 × 10 different badge codes.)
Answer:
Model with Mathematics Ian is going to flip a coin and roll a number cube 3,000 times. Use this information for Problems 18-20.
Question 18.
Write and solve a proportion to predict the number of times the coin lands on tails and the number cube lands on 5.
Answer:
Given that,
Ian is going to flip a coin and roll a number cube 3,000 times.
The number of times the coin lands on tails = 1/2
The probability for the coin lands on tails for 3000 times = 1/2 x 3000 = 1500 times
The Number cube lands on 5 are
The cube has 6 sides. So, the probability of the cube lands on 5 is 1/6
The probability for the cube lands on 5 for 3000 times = 1/6 x 3000 = 500 times.
Question 19.
Write and evaluate an expression to predict the number of times the coin lands on heads and the number cube lands on an even number.
Answer:
The coin has two sides.
The number of times the coin lands on heads is
The probability of the coin lands on heads = 1/2.
The probability for the coin lands on heads for 3000 times = 1/2 x 3000 = 1500 times.
In a cube there are 6 sides, In these 6 sides 3 numbers are even
The number of favorable outcomes for the even numbers is 3.
The probability of the number cube landing on an even number is = number of favorable outcomes/Total number of outcomes = 3/6 = 1/2.
The probability of the number cube landing on an even number for 3000 times = 1/2 x 3000 = 1500 times.
Question 20.
Write and evaluate an expression to predict the number of times the coin lands on tails and the number cube lands on a number greater than 2.
Answer:
Ian is going to flip a coin and roll a number cube 3,000 times.
The number of times the coin lands on tails = 1/2
The probability for the coin lands on tails for 3000 times = 1/2 x 3000 = 1500 times
The Number cube lands on a number greater than 2.
The cube has 6 sides. The greater than 2 are 3, 4, 5, and 6. So, the number of favorable outcomes is 4.
The probability of the cube landing on a number greater than 2 is = number of favorable outcomes/total number of outcomes = 4/6 = 2/3
The probability for the cube land on greater than 2 is for 3000 times = 2/3 x 3000 = 2000 times.
Question 21.
A box had 12 red tiles, 15 blue tiles, and 23 purple tiles. LaTanisha randomly selects a tile without looking 2,000 times. Each time a tile is selected, it is replaced before the next selection. Predict the number of times LaTanisha selects a blue or red tile.
Answer:
Lesson 15.3 More Practice/Homework
Question 1.
Oliver selects a glove from his drawer. The glove is blue. There are 3 red gloves, 6 black gloves, and 11 blue gloves left in the drawer. He selects a second glove from the drawer without looking. Is it likely that Oliver selects a glove of the same color? Explain your reasoning.
Answer:
Question 2.
If you roll a number cube 20 times, about how many times do you expect to roll a number greater than 4?
Answer:
Greater than 4 is 5 and 6
The number of events occurs is 2
Roll a number cube 20 times.
The probability of greater than 4 is = number of times events occur/ total number of trials = 2/20 = 1/10.
In the theoretical reasoning
The probability of greater than 4 is = number of favorable outcomes/total number of possible outcomes = 1/6.
Use Structure Victoria spins the two spinners shown 500 times. Use this information for Problems 3-5.
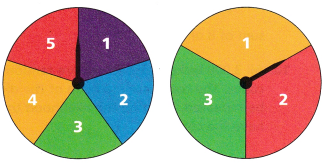
Question 3.
Solve a proportion to predict the number of times the sum is 4.
Answer:
Question 4.
Solve a proportion to predict the number of times the sum is 4, 5, or 6.
Answer:
Question 5.
Solve a percent equation to predict the number of times the sum is less than or equal to 3.
Answer:
Model with Mathematics There are 5 red, 18 green, and 17 blue pens in a bag. Leah selects a pen 800 times without looking. Before each selection, she replaces the pen in the bag. Use this information for Problems 6-7.
Question 6.
Write and evaluate an expression to predict the number of times Leah selects a pen that is red or green.
Answer:
Given that,
The total number of red pens in the bag = 5
The total number of green pens in the bag = 18
The total number of blue pens in the bag = 17
The total number of pens in the bag = 5 + 18 + 17 = 40
The total number of green and red pens = 5 + 18 = 23
The formula for the probability of green or red pens = number of green or red pens/ total number of green or red pens in the bag = 23/40
The probability of green or red pens for 800 times = 23/40 x 800 = 460 times.
Question 7.
Write and evaluate an expression to predict the number of times Leah selects a pen that is not red.
Answer:
Given that,
The total number of red pens = 5
The total number of pens in the bag = 5 + 18 + 17 = 40
The formula for the probability of red pens in the bag = number of red pens/ total number of pens in the bag = 5/40.
The probability for not red = 1 – 5/40 = 35/40 = 7/8
The probability for not red pens for 800 times = 7/8 x 800 = 700 times.
Test Prep
Question 8.
Leo has 10 red cards, 20 black cards, 20 yellow cards, and 25 white cards in a bag. He randomly selects a card 300 times. He replaces the card after each selection. Predict how often Leo will select a white card.
(A) about 12 times
(B) about 75 times
(C) about 100 times
(D) about 150 times
Answer:
Given that,
The number of red cards = 10
The number of black cards = 20
The number of yellow cards = 20
The number of white cards = 25.
Leo selects a card 300 times.
The Leo selects a white card = 300/25 = 12.
Option A is the correct answer.
Question 9.
Scarlet rolls a number cube labeled 1-6 and spins the spinner shown 2,100 times. Match the prediction to the correct event.

Answer:
Question 10.
All 3,000 lockers at a school are randomly assigned 3-digit combination codes. The codes are made up of the digits 0 through 9. The digits can be repeated. Describe the likelihood that fewer than 5 of the lockers will have the code 000.
Answer:
Given,
All 3,000 lockers at a school are randomly assigned 3-digit combination codes.
The codes are made up of the digits 0 through 9.
Analysis:
10 × 10 × 10 = 1000
We have 1000 situations in all.
P(The code is 000) = 1/1000
The school has 3000 lockers
3000 × 1/1000 = 3
3 is less than 5
3 < 5
So, fewer than 5 of the lockers will have the code 000.
Spiral Review
Question 11.
Levi rolled a number cube labeled 1-6. The number cube landed on 1 four times, 2 two times, 3 one time, 4 two times, 5 three times, and 6 six times. Which experimental probability is the same as the theoretical probability?
Answer:
Question 12.
Brianna rolls two number cubes labeled 1-6. What is the probability that Brianna rolls a sum of 5?
Answer:
Given that,
Brianna rolls two number cubes that are labelled as 1 – 6.
To get the sum of 5. The sample space is
n(s) = {(1,4), (4,1), (3,2), (2,3)}
The number of elements in n(s) = 4.
The number of possible outcomes is 6 x 6 = 36.
The formula for the probability P = The number of elements/number of possible outcomes.
P = 4/16 = 1/9.