We included HMH Into Math Grade 7 Answer Key PDF Module 15 Lesson 2 Find Theoretical Probability of Compound Events to make students experts in learning maths.
HMH Into Math Grade 7 Module 15 Lesson 2 Answer Key Find Theoretical Probability of Compound Events
I Can find the theoretical probability of a compound event.
Step It Out
Question 1.
Lucas spins the two spinners shown labeled 1 through 4. Spinning each number on one spinner is equally likely. He wants to find the probability that the sum of the two numbers he spins is 3.
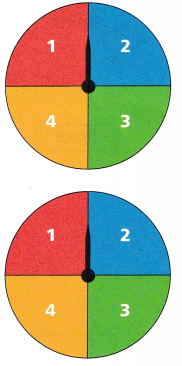
A. Lucas makes a table to represent the sample space of sums. Each entry in the table is the sum of the numbers in the corresponding row and column. Complete the remainder of the table.
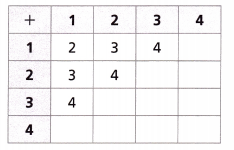
Answer:
Explanation:
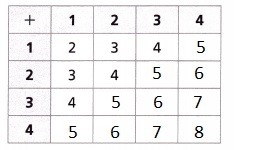
Lucas made a table to represent the sample space of sums. Each entry in the table is the sum of the numbers in the corresponding row and column. Completed the remainder of the table as shown above.
B. The table in Part A shows:
- There are _________ possible outcomes with a sum of 3.
- There are __________ equally likely outcomes in the sample space.
Answer:
There are 2 possible outcomes with a sum of 3, There are 5 equally likely outcomes in the sample space,
Explanation:
Using the data of table in Part A there are 2 possible outcomes with a sum of 3 one is 1 + 2 = 3 and other is 2 + 1 = 3. There are 5 equally likely outcomes in the same sample space they are 1. 3, 3, 2. 4, 4 , 4, 3. 5, 5, 5, 5, 4. 6, 6, 6, 5. 7, 7 respectively.
C. Find the theoretical probability of spinning a sum of 3.
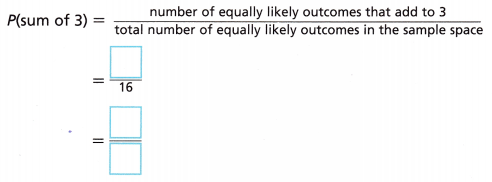
Answer:
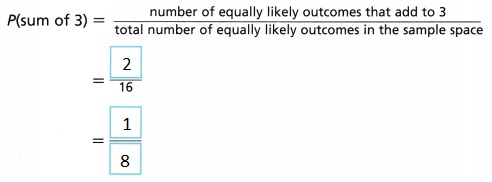
Explanation:
The theoretical probability of spinning a sum of 3 is p(sum of 3) = number of equally likely outcomes that add to 3/ total number of equally likely outcomes in the sample space = 2/16 = 1/8.
D. Determine another possible outcome in the sample space that has the same probability as that of spinning a sum of 3.
P (sum of 3) = P (___________)
Answer:
P (sum of 3) = 1/8,
Explanation:
Another possible outcome in the sample space that has the same probability as that of spinning a sum of 3 is number of equally likely outcomes that add to 3/ total number of equally likely outcomes in the sample space = 2/16 = 1/8.
Question 2.
Aria can choose one pair of shorts (black or white), one shirt (red, blue, or green), and one pair of shoes (brown or tan) as her outfit. Find the probability of choosing an outfit at random and getting white shorts, a blue shirt, and tan shoes.

A. Complete the tree diagram to represent the sample space.
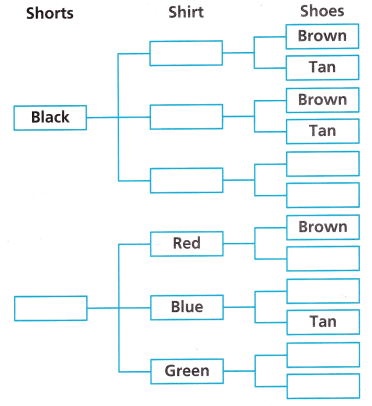
Answer:
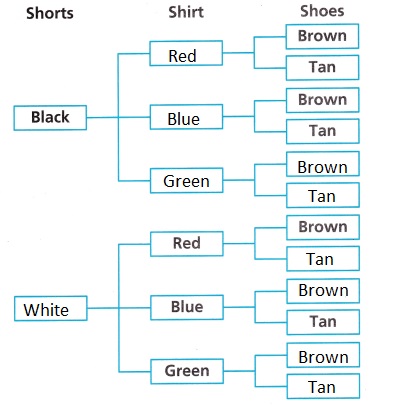
Explanation:
Completed the tree diagram to represent the sample space as shown above.
B. The tree diagram shows that there are _________ equally likely outcomes in the sample space.
Answer:
No, equally likely outcomes in the sample space,
Explanation:
The tree diagram shows that there are no equally likely outcomes in the sample space.
C. Find the probability P(white, blue, tan).
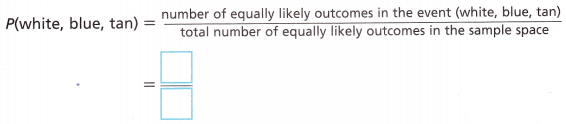
Answer:
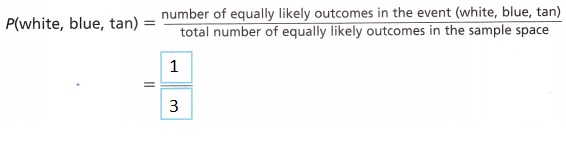
Explanation:
The probability P(white, blue, tan) = number of equally likely outcomes in the event(white, blue, tan)/ total number of equally likely outcomes in the sample space = 1/3.
D. Find the probability of selecting white shorts and a blue shirt when selecting clothes at random.
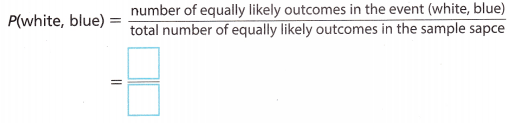
Answer:
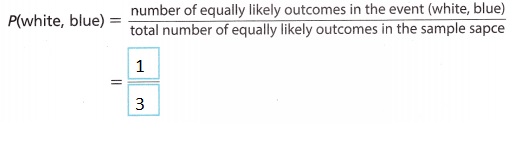
Explanation:
The probability of selecting white shorts and a blue shirt when selecting clothes at random is number of equally likely outcomes in the event(white, blue)/ total number of equally likely outcomes in the sample space = 1/3.
Question 3.
Ali draws cards from a hat that contains three cards labeled Winning Combination A, B, and C. He has an equal chance of drawing each card. He draws one card at a time, records the result, and replaces it before the next draw. Ali wins a prize for drawing the A-card 3 times in a row. What is the probability that he wins a prize?
A. Complete the organized lists to represent the sample space.
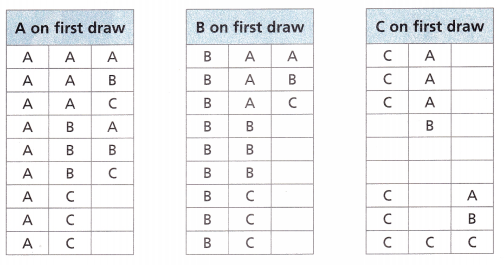
Answer:
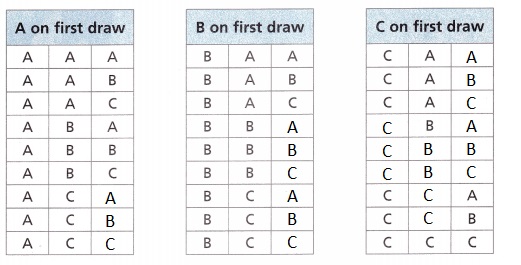
Explanation:
Given Ali draws cards from a hat that contains three cards labeled Winning Combination A, B, and C. He has an equal chance of drawing each card. He draws one card at a time, records the result, and replaces it before the next draw. Ali wins a prize for drawing the A-card 3 times in a row.
Completed the organized lists to represent the sample space as shown above.
B. The organized lists show that there are ____________ equally likely outcomes in the sample space.
Answer:
The organized lists show that there are no equally likely outcomes in the sample space.
C. Find the probability P(A, A, A). Write the probability as a fraction, decimal, and percent. Round to the nearest hundredth and whole percent.

The probability that Ah wins a prize is about ___________ %.
Answer:

The probability that Ah wins a prize is about 4%,
Explanation:
The probability P(A, A, A) is number of equally likely outcomes in the event(A,A,A)/ Tootal number of equally likely outcomes in the sample space = 1/27 or 0.0370 or 3.7% or 4%.
Turn and Talk How do you think you could use the organized lists to find the probability of drawing 2 or more A-cards in any order?
Answer:
By checking the organized list and by counting the probability of drawing 2 or more A-cards in any order,
Explanation:
Simply by checking the organized list and by counting the probability of drawing 2 or more A-cards in any order we get 1. A, A, A, 2. A, A, B, 3. A, A, C, 4. B, A, A, 5. C, A, A.
Check Understanding
Question 1.
What are some ways that you can represent the sample space of a compound event?
Answer:
The three most common ways to find a sample space are:
To list all the possible outcomes, Create a Tree- Diagram, Use a Venn diagram,
Explanation:
If an event has more than one possible outcome, the event is called a compound event. A sample space is the set of all possible outcomes for an experiment. When determining a sample space, we must be careful to include all possibilities. Therefore the three most common ways to find a sample space are: To list all the possible outcomes, Create a Tree- Diagram, Use a Venn diagram.
Question 2.
Mila spins two spinners. One spinner has two equal sections labeled 1 and 2. The other spinner has three equal sections labeled 1, 2, and 3. What is the probability that the sum of the two spins is 4?
Answer:
The probability that the sum of the two spins is 4 is 2,
Explanation:
Given Mila spins two spinners. One spinner has two equal sections labeled 1 and 2. The other spinner has three equal sections labeled 1, 2, and 3. The probability that the sum of the two spins is 4 is
one spinner – 1, 2, 1
other spinner – 1, 2, 3
(+) 4, 4 is 2.
On Your Own
Question 3.
Use Structure Wyatt rolls two number prisms in the shape of triangular prisms, labeled 1 to 3 as shown.

A. Complete the table to represent the sample space for the sum of these two number prisms.
Answer:
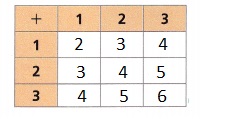
Explanation:
Completed the table to represent the sample space for the sum of these two number prisms as shown above.
B. What is the probability that Wyatt rolls a sum of 3?
Answer:
The probability that Wyatt rolls a sum of 3 is 2,
Explanation:
The probability that Wyatt rolls a sum of 3 is 1 + 2 = 3 and 2 + 1 = 3 so it is 2.
C. What event has the same probability as rolling a sum of 3? Explain.
Answer:
Event 1 + 2 = 3,
Explanation:
Event 1 + 2 = 3 has the same probability as rolling a sum of 3.
D. Name an event that is less likely than a sum of 3. Explain.
Answer:
Event 1 + 1 = 2,
Explanation:
Event 1 + 1 = 2 has less likely than a sum of 3.
E. Name an event that is more likely than a sum of 3. Explain.
Answer:
Event 1 + 3, Event 2 + 2, Event 2 + 3, Event 3 + 1, Event 3 + 2, Event 3 + 3,
Explanation:
Event 1 + 3 = 4, Event 2 + 2 = 4, Event 2 + 3 = 5, Event 3 + 1 = 4, Event 3 + 2 = 5, Event 3 +3 = 6 are more likely than a sum of 3.
Model with Mathematics Find each probability. Give your answer as a simplified fraction, a decimal to the nearest hundredth, and a percent to the nearest whole percent.
F. P(sum of 4)
Answer:
3,
Explanation:
The P(sum of 4) is Event 1 + 3 = 4, Event 2 + 2 = 4 and Event 3 + 1 = 4.
G. P(sum of 6)
Answer:
Event 3 + 3,
Explanation:
The P(sum of 6) is Event 3 + 3 = 6.
H. P(sum < 10)
Answer:
Event 1 + 1, Event 1 + 2, Event 1 + 3, Event 2 + 1, Event 2 + 2, Event 2 + 3, Event 3 + 1, Event 3 + 2, Event 3 + 3,
Explanation:
P(sum < 10) all these events have probability of sum less than 10 Event 1 + 1 = 2, Event 1 + 2 = 3, Event 1 + 3 = 4, Event 2 + 1 = 3, Event 2 + 2 = 4, Event 2 + 3 = 5, Event 3 + 1 = 4, Event 3 + 2 = 5, Event 3 + 3 = 6.
I. P(sum > 10)
Answer:
Zero,
Explanation:
There is no event where the probability of sum is greater than 10.
Question 4.
Use Structure Layla tosses three coins.

A. Complete the tree diagram to show the sample space for how the coins can land. H represent heads and T represents tails.
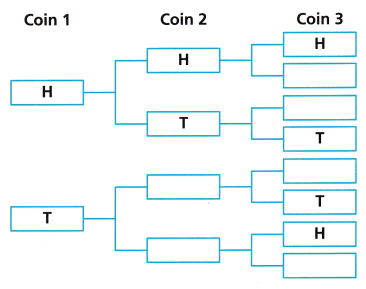
Answer:
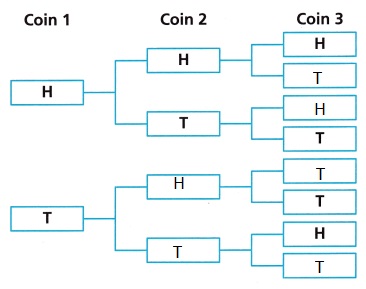
Explanation:
Completed the tree diagram to show the sample space for how the coins can land. H represent heads and T represents tails above.
B. What is the probability that exactly two coins land heads up? Write the probability as a fraction, decimal, and percent.
Answer:
2/8, 0.25, 25%,
Explanation:
The probability that exactly two coins land heads up is 1/8 and 1/8 so the probability as a fraction is 1/8 + 1/8 = 2/8 = 1/4 as decimal is 0.25 and percent is 0.25 X 100 = 25%.
C. What is the probability that exactly two coins land tails up? Compare this probability to the probability that exactly two coins land heads up.
Answer:
3/8 and 2/8 probability of tails up is more than heads up,
Explanation:
The probability that exactly two coins land tails up is 1/8 + 2/8 = 3/8, now comparing this probability to the probability that exactly two coins land heads up is 3/8 > 2/8.
D. What is the probability that exactly three coins land tails up? Write the probability as a fraction, decimal, and percent.
Answer:
1/8, 0.125, 12.5,
Explanation:
The probability that exactly three coins land tails up is 1/8, the probability as a fraction is 1/8 decimal, is 0.125 and percent is 12.5.
E. Name an event with the same probability as that of three tails? Explain.
Answer:
Event (T, T, T),
Explanation:
An event with the same probability as that of three tails is event (T, T, T).
F. Compare the theoretical probability of getting at least one head and the theoretical probability of getting at least two tails.
Answer:
The theoretical probability of getting at least one head is less than the theoretical probability of getting at least two tails,
Explanation:
The theoretical probability of getting at least one head is 1/8 and the theoretical probability of getting at least two tails is 3/8 now comparing the theoretical probability of getting at least one head is less than the theoretical probability of getting at least two tails is 1/8 < 3/8.
Question 5.
Use Structure Daniel is going to spin the spinner shown and roll a number cube.
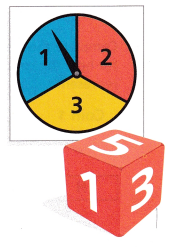
A. Make an organized list to show the sample space for spinning the spinner and rolling the number cube.
Answer:
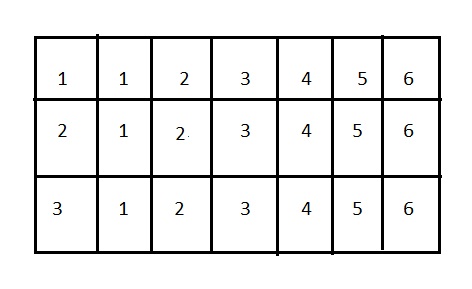
Explanation:
Made an organized list to show the sample space for spinning the spinner and rolling the number cube above.
B. What is the probability that Daniel gets a sum of 5?
Answer:
3/21 or 1/7,
Explanation:
The probability that Daniel gets a sum of 5 is 1 + 4, 2 + 3, 3 + 2 so it is 3/21 or 1/7.
C. What is the probability that Daniel gets a sum of 3?
Answer:
2/21,
Explanation:
The probability that Daniel gets a sum of 3 is 1 + 2, 2 + 1 is 2/21.
D. Compare the probability of getting a sum of 5 and getting a sum of 3.
Answer:
The probability of getting a sum of 5 is more likely than getting a sum of 3,
Explanation:
The probability of getting a sum of 5 and getting a sum of 3 is the probability that Daniel gets a sum of 5 is 1 + 4, 2 + 3, 3 + 2 so it is 3/21 and the probability that Daniel gets a sum of 3 is 1 + 2, 2 + 1 is 2/21 so comparing 3/21 is more likely than 2/21 means sum of 5 is more likely than getting a sum of 3.
E. Open-Ended Give an example of an event that is more likely than getting a sum of 8. Explain your reasoning.
Answer:
Event 2 + 6 or Event 3 + 5,
Explanation:
An event that is more likely than getting a sum of 8 is event 2 + 6 or event 3 + 5.
F. Open-Ended Give an example of an event that is as equally likely as getting a sum of 6. Explain your reasoning.
Answer:
Event 1 + 5 or Event 2 + 4 or Event 3 + 3,
Explanation:
Event 1 + 5 or Event 2 + 4 or Event 3 + 3 are examples of an event that is as equally likely as getting a sum of 6.
Question 6.
Reason How is finding the theoretical probability of a compound event similar to finding the theoretical probability of a simple event?
Answer:
Compound Probability describes the chances of more than one separate event occurring, for example flipping heads on a coin and pulling a 7 from a standard deck of cards,
Simple probability expresses the probability of one event occurring and is often visually expressed using coins, dice, marbles or spinner.
Number of favorable outcomes over the number of total outcomes.
Explanation:
Compound event consists of two or more simple events. To find the probability of a compound event, we write a ratio of the number of ways the compound event can happen to the total number of equally likely possible outcomes.
The probability of simple events is finding the probability of a single event occurring. When finding the probability of an event occurring, we will use the formula: number of favorable outcomes over the number of total outcomes. After calculating this probability.
Lesson 15.2 More Practice/Homework
Question 1.
Use Structure Christian has a red box with tiles numbered from 1 to 5 and a green box with tiles numbered from 1 to 3. He draws a tile from each box, and then finds the sum.

A. Make a table to represent the sample space for drawing a particular sum from the numbers in the two boxes.
Answer:
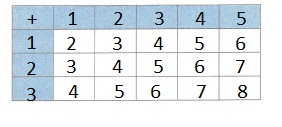
Explanation:
Made a table to represent the sample space for drawing a particular sum from the numbers in the two boxes as shown above.
B. What is the probability of drawing a sum of 7?
Answer:
2/15,
Explanation:
The probability of drawing a sum of 7 is 2/15.
C. Name an event that is more likely than drawing a sum of 7.
Answer:
Event 2 + 5 or Event 3 + 4,
Explanation:
An event that is more likely than drawing a sum of 7 is Event 2 + 5 or Event 3 + 4.
Question 2.
Use Structure Lucy can choose one sandwich (ham or turkey), one side (apples or grapes), and one drink (milk or water). Lucy has an equally likely chance of choosing any combination.
A. Make a tree diagram to find the Sandwich Side sample space.
Answer:
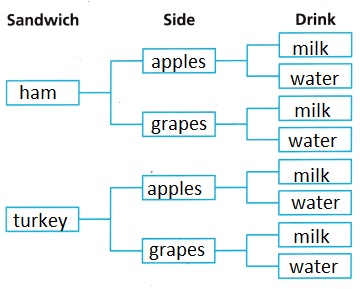
Explanation:
Made a tree diagram to find the Sandwich Side sample space as sown above.
B. What is the probability Lucy picks a ham sandwich and grapes?
Answer:
1/2,
Explanation:
The probability Lucy picks a ham sandwich and grapes is out of two sides it is one so it is 1/2.
C. What is the probability Lucy chooses milk with a turkey sandwich and apples?
Answer:
1/8,
Explanation:
The probability Lucy chooses milk with a turkey sandwich and apples is 1/8.
D. Reason Name an event that is equally as likely as choosing ham and apples.
Answer:
Event (ham, apples, milk) or Event (ham, apples, water),
Explanation:
An event that is equally as likely as choosing ham and apples is Event (ham, apples, milk) or Event (ham, apples, water).
Question 3.
Attend to Precision How many different possible outcomes are there for the experiment described here?
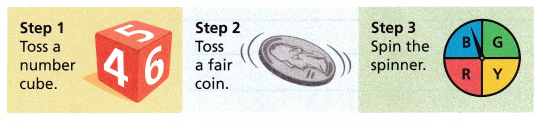
There are ___________ different possible outcomes.
Answer:
There are 1/6, 1/2 and 1/4 different possible outcomes,
Explanation:
Different possible outcomes are there for the experiment described are
step 1 : tossing a number cube it is 1/6,
step 2 : tossing a fair coin it is 1/2,
step 3 : spinning the spinner it is 1/4 .
Test Prep
Question 4.
Emma is going to flip a coin, resulting in H for heads or T for tails, and spin the spinner shown. Which list correctly represents the sample space?
(A) H, T, 1,2,3,4, 5, 6
(B) H-1, H-2, H-3, H-4, H-5, H-6
(C) H-1, H-2, H-3, H-4, H-5, H-6, T-1, T-2, T-3, T-4, T-5, T-6
(D) H-T-1, H-T-2, H-T-3, H-T-4, H-T-5, H-T-6
Answer:
(C) H-1, H-2, H-3, H-4, H-5, H-6, T-1, T-2, T-3, T-4, T-5, T-6,
Explanation:
Given Emma is going to flip a coin, resulting in H for heads or T for tails, and spin the spinner shown. the list correctly represents the sample space is (C) H-1, H-2, H-3, H-4, H-5, H-6, T-1, T-2, T-3, T-4, T-5, T-6.
Question 5.
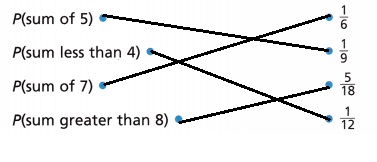
Luna rolls two number cubes labeled 1-6. Match the probability to the correct event.

Answer:
Explanation:
Given Luna rolls two number cubes labeled 1-6. Matching the probability to the correct event as
P(sum of 5) is 4/36 = 1/9,
P(sum less than 4) is 1/12,
P(sum of 7) is 1/6,
P(sum greater than 8) is 5/18 above.
Question 6.
Carson can choose one vehicle (car or truck), one color (blue, red, or silver), and one type of transmission (standard or automatic). How many possible outcomes are there?
Answer:
1/12,
Explanation:
Given Carson can choose one vehicle (car or truck), one color (blue, red, or silver), and one type of transmission (standard or automatic). Number of possible outcomes are there are
1. car, blue, standard, 2. car, blue, automatic, 3. car, red, standard, 4. car, red, automatic, 5. car, silver, standard, 6. car, silver, automatic, 7. truck, blue, standard, 8. truck, blue, automatic, 9. truck, red, standard, 10. truck, red, automatic, 11. truck, silver, standard, 12. truck, silver, automatic.
Spiral Review
Question 7.
Aaliyah spins the spinner shown. What is the theoretical probability that the spinner will land on an even number?

Answer:
4/9,
Explanation:
Given Aaliyah spins the spinner shown. The theoretical probability that the spinner will land on an even number is out of 9 we have even numbers are 2,4,6,8 so it is 4/9.
Question 8.
Tell whether the following relationship is a proportional relationship. Explain why or why not. If it is, identify the unit rate.

Answer:
Yes proportional relationship, Unit rate is 40,
Explanation:
Given a relationship we check it is proportional or not as
1. 120/ 3 = 40, 2. 200/5 = 40, 3. 320/8 = 40, 4. 400/10 = 40 so it is clear that for 1 minute words typed are 40 therefore ii is proportional and the unit rate is 40.