We included HMH Into Math Grade 7 Answer Key PDF Module 15 Lesson 1 Find Theoretical Probability of Simple Events to make students experts in learning maths.
HMH Into Math Grade 7 Module 15 Lesson 1 Answer Key Find Theoretical Probability of Simple Events
I Can find the theoretical probability of a simple event.
Spark Your Learning
Dominic wants to play a balloon dart game at the county fair. He can play Game 1 or Game 2. If he pops a blue balloon with a dart, he wins a prize. Which game should Dominic play if he wants a better chance of winning a prize? Assume that Dominic gets one throw, and it will hit a balloon in either game.

Answer:
The total number of balloons in the game 1 = 12
In the game 1 the number of blue balloons = 4
The probability of the blue balloons in the game 1 = 4/12 = 1/3 = 33%
The total number of balloons in the game 2 = 8
In the game 2 the number of blue balloons = 2
The probability of the blue balloons in the game 2 = 2/8 = 1/4 = 25%
Game 1 is the better choice for Dominic to win a prize. Because game 1 has more blue balloons then game 2.
Dominic gets one throw, and it will hit a balloon in either game but there are more chances in game 1.
Turn and Talk Explain what changes could be made to Game 1 so that Dominic has the same chance of winning a prize when playing either game.
Answer:
Reduce 1 blue balloon in the game 1 then Dominic has the same chance of winning a prize when playing either game.
The total number of balloons in the game 1 = 12
In the game 1 the number of blue balloons = 3
The probability of the blue balloons in the game 1 = 3/12 = 1/4 = 25%
The total number of balloons in the game 2 = 8
In the game 2 the number of blue balloons = 2
The probability of the blue balloons in the game 2 = 2/8 = 1/4 = 25%
Build Understanding
Question 1.
Clara is playing a game where she chooses to spin one of the spinners shown. If the spinner lands on a section labeled “A,” she wins a pair of headphones. Which spinner will give her the best chance of winning?
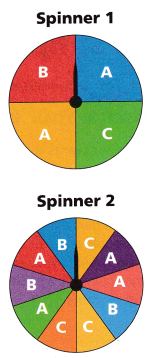
A. Total number of sections for each spinner:
Spinner 1 has a total of ___________ sections of the same area.
Spinner 2 has a total of ___________ sections of the same area.
Answer:
Spinner 1 has a total of 4 sections of the same area.
Spinner 2 has a total of 10 sections of the same area.
B. Number of sections labeled “A” for each spinner:
Spinner 1 has ___________ sections labeled “A”.
Spinner 2 has ___________ sections labeled “A”.
Answer:
Spinner 1 has 2 sections labeled “A”
Spinner 2 has 4 sections labeled “A”
C. What is the ratio of sections labeled “A” to total number of sections for each spinner?

Answer:
The total number of sections labeled “A” in the spinner 1 = 2
The total number of sections in the spinner 1 = 4
The ratio of sections labeled “A” to the total number of sections for spinner 1 = 2/4 = 1/4.
The total number of sections labeled “A” in the spinner 2 = 4
The total number of sections in the spinner 2 = 10
The ratio of sections labeled “A” to the total number of sections for spinner 2 = 4/10 = 2/5.
D. How can you make the ratios in Part C easier to compare?
Answer:
By using the theoretical probability for the sections labeled “A” is the easier way to find the ratios in part C.
E. What is the ratio of sections labeled “A” to total number of sections for each spinner, written as fractions with a common denominator?

Answer:
Spinner 1 has 20 sections. It means 4 = 20
The spinner 2 has 20 sections. It means 10 = 20
Spinner 1 has 2 sections labeled “A”
Spinner 2 has 4 sections labeled “A”
The ratio of sections labeled “A” to the total number of sections in spinner 1 = 10/20 = 1/2.
The ratio of sections labeled “A” to the total number of sections in spinner 2 = 8/20 = 2/5.
F. Which spinner should Clara spin to give her the best chance of winning a pair of headphones? Explain.
Answer:
The spinner 1 should Clara spin to give her the best chance of winning a pair of headphones. Because the probability of spinner 1 labeled A = 2/4 = 1/2.
There are more chances to get the headphones by spinning the spinner 1.
G. Which spinner should Clara spin to give her the best chance of landing on “C”? Explain.
Answer:
Spinner 2 should spin Clara to give her the best chance of landing on “C” because the number of possible ways in the spinner 1 to land on C is 1/4.
The number of possible ways in the spinner 2 landing on C is 3/10.
The best choice is the spinner 2.
Turn and Talk Describe another way to compare the ratios in Part C.
Answer:
Step It Out
If the outcomes of an experiment are equally likely, you can find the theoretical probability of an event without performing the experiment.
![]()
Connect to Vocabulary
If all possible outcomes are equally likely, the theoretical probability of an event is the ratio of the number of possible outcomes in the event to the total number of possible outcomes in the sample space.
When a probability is given as a fraction, it is usually written in the simplest form.
Question 2.
Lindsay is going to draw one tile from the bag shown without looking. The tiles are the same size and cannot be told apart by touch, so each tile has an equal chance of being chosen. What is the theoretical probability that she selects a red tile?
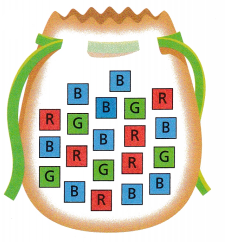
A. Identify the sample space.
5 (red / blue / green) tiles
6 (red / blue / green) tiles
9 (red / blue / green) tiles
Answer:
The total number of tiles = 20
The total number of red tiles = 5
Probability of red tiles = number of red tiles/total number of tiles = 5/20 = 1/4.
Therefore the probability of red tile is 1/4.
The sample space is 5(red/blue/green) tiles.
B. Find the total number of equally likely possible outcomes in the sample space by adding.

There are ___________ equally likely outcomes in the sample space.
Answer:
Given that,
Green tiles +red tiles + blue tiles = total number of tiles
5 + 6 + 9 = 20
There are 20 equally likely outcomes in the sample space.
C. Identify the total number of possible outcomes included in the event “select a red tile.” Is each possible outcome equally likely?
There are ___________ red tiles in the bag, so there are possible outcomes included in this event. Each of these possible outcomes (is / is not) equally likely.
Answer:
There are 5 red tiles in the bag, so there are possible outcomes included in this event. Each of these possible outcomes is equally likely.
D. Find the theoretical probability that Lindsay will select a red tile. Then, write the ratio in simplest form.

Answer:
Given that,
The total number of tiles = 20
The total number of red tiles = 5
Probability of red tile = number of red tiles/total number of tiles = 5/20 = 1/4.
Therefore the probability of a red tile is 1/4.
E. Probability can be written as a fraction, decimal, or percent. Write the theoretical probability that Lindsay draws a red tile from the bag as a fraction, a decimal, and a percent.
Answer:
Given that,
The total number of tiles = 20
The total number of red tiles = 5
Probability of red tile = number of red tiles/total number of tiles = 5/20 = 1/4.
The probability of red tiles in the fraction is 1/4.
The probability of red tiles in decimal = 0.25
The probability of red tiles in percent = 25%
Question 3.
Miguel is deciding if he should do his chores or homework first. To help him decide, he flips a coin.

A. Miguel flips the coin once. Find the theoretical probability of the coin landing on heads and the theoretical probability of the coin landing on tails. Write each as a decimal.
P(Heads) = ![]()
P(Tails) = ![]()
Answer:
The coin has two sides; one is the head and the other is the tail.
The theoretical probability of the coin landing on heads = 1/2.
The theoretical probability of the coin landing on tails = 1/2.
B. Predict the number of times the coin will land on heads and tails out of 20 flips using the theoretical probability.
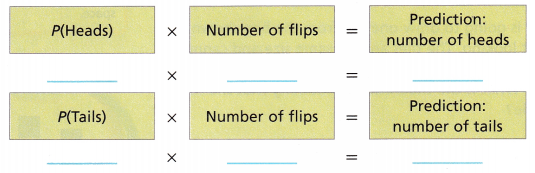
Answer:
P(heads) = 1/2
P(tails) = 1/2.
The total number of flips = 20
Prediction: number of heads = 1/2 x 20 = 10
Prediction: number of heads = 1/2 x 20 = 10
C. Flip a coin 20 times. Record the outcomes in the frequency column. Then give the experimental probability to the nearest percent.

Answer:
Flip a coin = 20 times
The coin has 2 sides.
The frequency of a coin landing on the head = 20/2 = 10
The frequency of a coin landing on the tail = 20/2 = 10
The experimental probability of a coin landing on heads = 1/10 = 10%
The experimental probability of a coin landing on the tail = 1/10 = 10%

D. Compare the theoretical and experimental probabilities of the coin landing on heads and tails. Are the probabilities equal? Why isn’t experimental probability always the same as theoretical probability?
Answer:
The theoretical and experimental probabilities of the coin landing on heads and tails are the same. The theoretical probability of the event is the same but the experimental probability of an event is different.
Check Understanding
Question 1.
Eric’s coach said he could spin a spinner with 4 equal sections labeled 1-4, or roll a number cube labeled 1-6. If Eric gets a 1, he does not have to run a sprint. If Eric does not want to run a sprint, which should he pick? Explain.
Answer:
Given that,
The spinner with 4 sections
The die with 6 sections.
Eric gets a 1he does not have to run a sprint. If Eric does not want to run a sprint
The probability of the spinner getting 1 = 1/4 = 25%
The probability of the die getting 1 = 1/6 =16%
Eric has more chances of choosing of getting 1 in the spinner.
Question 2.
Pam tossed a coin 50 times and found the probability of getting heads was 45%. Was this a theoretical or experimental probability? Explain.
Answer:
On Your Own
Question 3.
Use Structure Amara has the choice to select one card from Pile 1 or Pile 2 without looking. If she selects a yellow card, she wins the game. Which pile should Amara pick from to give her a better chance of winning? Explain your reasoning.
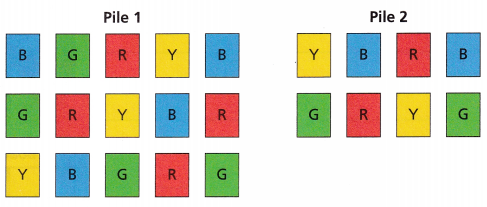
Answer:
The total number of cards in the Pile 1 = 15
The total number of yellow cards in the pile 1 = 3
The total number of Cards in the pile 2 = 8
The total number of yellow cards in the pile 2 = 2
The probability of yellow card in the pile 1 = 3/15 = 1/5 = 20%
The probability of yellow card in the pile 2 = 2/8 = 1/4 = 25%
Amara picks from to give her a better chance of winning in Pile 2. Because the probability of Pile 2 is greater than Pile 1. So, there are more chances to get a yellow card.
Question 4.
Reason The table shows the results of rolling a number cube 50 times. Compare the experimental probability and theoretical probability of rolling a 5. Give a possible reason why the probabilities are different.

Answer:
The formula for the experimental probability = number of times an event occurs/total number of trials.
The experimental probability of rolling a 5 = 7/50
The formula for the theoretical probability = number of favorable outcomes/total number of possible outcomes.
The theoretical probability of rolling a 5 = 1/6
The experimental and theoretical probability is different. Because the experimental probability is based on the actual results of the experiment and the theoretical probability is based on the number of possible outcomes on the assumptions.
For Problems 5-8, use the gift boxes shown. Find the theoretical probability of randomly selecting each gift box. Write the probability as a fraction in simplest form.

Question 5.
yellow box: ![]()
Answer:
The formula for the theoretical probability = number of favorable outcomes/total number of possible outcomes.
The total number of possible outcomes = number of boxes = 8
The number of favorable outcomes for the yellow box = number of yellow boxes = 1
The theoretical probability for the yellow box = number of favorable outcomes/total number of possible outcomes = 1/8.
Therefore yellow box = 1/8.
Question 6.
purple box: ![]()
Answer:
The formula for the theoretical probability = number of favorable outcomes/total number of possible outcomes.
The total number of possible outcomes = number of boxes = 8
The number of favorable outcomes for the purple box = number of purple boxes = 2
The theoretical probability for the purple box = number of favorable outcomes/total number of possible outcomes = 2/8 = 1/4.
Therefore purple box = 1/4.
Question 7.
blue box: ![]()
Answer:
The formula for the theoretical probability = number of favorable outcomes/total number of possible outcomes.
The total number of possible outcomes = number of boxes = 8
The number of favorable outcomes for the blue box = number of blue boxes = 1
The theoretical probability for the blue box = number of favorable outcomes/total number of possible outcomes = 3/8.
Therefore blue box = 3/8.
Question 8.
green box: ![]()
Answer:
The formula for the theoretical probability = number of favorable outcomes/total number of possible outcomes.
The total number of possible outcomes = number of boxes = 8
The number of favorable outcomes for the green box = number of green boxes = 1
The theoretical probability for the green box = number of favorable outcomes/total number of possible outcomes = 2/8 = 1/4.
Therefore green box = 1/4.
Question 9.
A bag contains 5 red balls, 8 white balls, and 7 black balls. What is the theoretical probability of randomly selecting a black ball from the bag?
Answer:
Given that,
The total number of red balls = 5
The total number of white balls = 8
The total number of black balls = 7
The formula for the theoretical probability = number of favorable outcomes/total number of possible outcomes.
The total number of possible outcomes = number of balls = 5 + 8 + 7 = 20
The number of favourable outcomes for the black ball = number of black balls = 5
The theoretical probability for the black ball from the bag = number of favourable outcomes/total number of possible outcomes = 5/20 = 1/4.
Question 10.
Chase can spin a spinner centered on Board 1 or Board 2. He wants the spinner to land on a section labeled “R.” Which board should he choose? Explain.
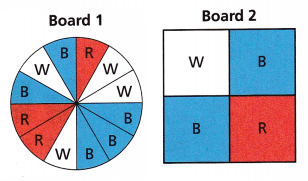
Answer:
The total number of sections in the Board 1 = 12
The Total number of R in the Board 1 = 3
The total number of sections in the Board 2 = 4
The total number of R in the Board 2 = 1
The probability of R in the Board 1 = 3/12 = 25%
The probability of R in the Board 2 = 1/4 = 25%
He can choose any board from Board 1 and Board 2. Because both boards have the same probability of 25.
Question 11.
Edith spun a spinner with 5 equal sections labeled 1-5. The spinner landed on 1 five times, on 2 three times, on 3 four times, on 4 three times, and on 5 five times. For which number is the experimental probability the same as its theoretical probability? Explain.
Answer:
Use Structure For Problems 12-13, use the flowers shown. Find the theoretical probability of selecting the color listed. Write the probability as a fraction in simplest form, a decimal, and a percent.

Question 12.
orange flower
Answer:
The formula for the theoretical probability = number of favorable outcomes/total number of possible outcomes.
The total number of possible outcomes = number of flowers = 10
The number of favorable outcomes for the orange flower = number of orange flowers = 4
The theoretical probability for the orange flowers = number of favorable outcomes/total number of possible outcomes = 4/10 = 2/5.
Therefore the theoretical probability of an orange flower = 2/5 or 0.4 or 40%
Question 13.
purple flower
Answer:
The formula for the theoretical probability = number of favorable outcomes/total number of possible outcomes.
The total number of possible outcomes = number of flowers = 10
The number of favorable outcomes for the purple flower = number of purple flowers = 6
The theoretical probability for the purple flowers = number of favorable outcomes/total number of possible outcomes = 6/10 = 3/5.
Therefore the theoretical probability of a purple flower = 3/5 or 0.6 or 60%
I’m in a Learning Mindset!
Was finding theoretical probabilities of simple events an appropriate challenge for me?
Answer:
Lesson 15.1 More Practice/Homework
Without looking, Luke picks necklace beads from a bag of 52 beads. Half the beads are rough. The other half are smooth. There are 13 red beads, 13 blue beads, 13 green beads, and 13 black beads. Use this information for Problems 1-5. Write each probability as a fraction in simplest form.
Question 1.
What is the theoretical probability of selecting a smooth bead?
Answer:
Given that,
The total number of beads = 52
The total number of rough beads = 52/2 = 26
The total number of smooth beads = 26
The total number of red beads = 13
The total number of blue beads = 13
The total number of green beads = 13
The total number of black beads = 13.
The theoretical probability for the smooth beads = number of smooth beads/total number of beads = 26/52 = 1/2.
Therefore the theoretical probability for the smooth beads = 1/2.
Question 2.
What is the theoretical probability of selecting a blue bead?
Answer:
Given that,
The total number of beads = 52
The total number of rough beads = 52/2 = 26
The total number of smooth beads = 26
The total number of red beads = 13
The total number of blue beads = 13
The total number of green beads = 13
The total number of black beads = 13.
The theoretical probability for the blue beads = number of blue beads/total number of beads = 13/52 = 1/4.
Therefore the theoretical probability for the blue beads = 1/4.
Question 3.
What is the theoretical probability of selecting a rough bead?
Answer:
Given that,
The total number of beads = 52
The total number of rough beads = 52/2 = 26
The total number of smooth beads = 26
The total number of red beads = 13
The total number of blue beads = 13
The total number of green beads = 13
The total number of black beads = 13.
The theoretical probability for the rough beads = number of rough beads/total number of beads = 26/52 = 1/2.
Therefore the theoretical probability for the rough beads = 1/2.
Question 4.
What is the theoretical probability of not selecting a red bead?
Answer:
Given that,
The total number of beads = 52
The total number of rough beads = 52/2 = 26
The total number of smooth beads = 26
The total number of red beads = 13
The total number of blue beads = 13
The total number of green beads = 13
The total number of black beads = 13.
The theoretical probability for the red beads = number of red beads/total number of beads = 13/52 = 1/4.
The theoretical probability for not selecting red beads = 1 – 1/4 = 3/2.
Therefore, the theoretical probability for the not red beads = 3/2
Question 5.
Reason One hundred times, Luke picks one bead then puts it back into the bag. The results are shown. What are the experimental probability and theoretical probability of picking a black bead? Name a possible reason why the probabilities are not the same.

Answer:
The formula for the experimental probability = number of times an event occurs/total number of trials.
The experimental probability of black bead = 20/100
The formula for the theoretical probability = number of favorable outcomes/total number of possible outcomes.
The theoretical probability of heads = 1/4.
The experimental and theoretical probability is not the same. Because the experimental probability is based on the actual results of the experiment and the theoretical probability is based on the number of possible outcomes on the assumptions.
Question 6.
Math on the Spot Find the probability of the event. Write your answer as a fraction, as a decimal, and as a percent.
A. draw one of the 4 L’s from a bag of 100 letter tiles
Answer:
Given that,
Draw one of the 4 L’s.
The total number of letters in the bag = 100
The probability of the event = 4/100 = 0.04
B. roll a number less than 4 on a number cube
Answer:
The numbers less than 4 are 1 or 2 or 3.
The total number of sides in the cube is 6
The probability of the event is 1/6.
Test Prep
Question 7.
Brice can win a game by selecting a letter tile with the letter B from a bag. He wants to choose a bag that will give him the best chance of winning. Which statement is correct?
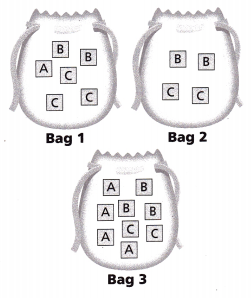
(A) Brice has the best chance only with Bag 1.
(B) Brice has the best chance only with Bag 2.
(C) Brice has the best chance only with Bag 3.
(D) Brice has the best chance with either Bag 1 or Bag 3.
Answer:
Question 8.
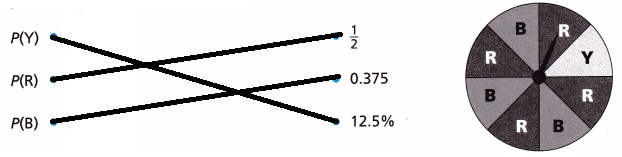
Use the spinner to match the theoretical probability to the correct event.

Answer:
The total number of sections in the spinner = 8
The total number of Y = 1
The total number of R = 4
The total number of B = 3
The probability of p(Y) = 1/8 = 1.25%
The probability of p(R) = 4/8 = 1/2.
The probability of p(B) = 3/8 = 0.375
Question 9.
The table shows the results of flipping a coin 10 times. How do the theoretical and experimental probabilities of the coin landing on heads compare?

Answer:
The formula for the experimental probability = number of times an event occurs/total number of trials.
The experimental probability of heads = 3/10
The formula for the theoretical probability = number of favorable outcomes/total number of possible outcomes.
The theoretical probability of heads = 1/2.
Spiral Review
Question 10.
A soccer team made 2 goals out of 32 attempts in a game. What is the experimental probability that the team made a goal on any given shot? Write the probability as a decimal.
Answer:
Given that,
The number of goals that the team made = 2
The number of attempts in a game = 32
The formula for the experimental probability = number of times an event occurs/total number of trials.
The experimental probability that the team made a goal on any given shot = The number of goals/number of outcomes = 2/32 = 1/16 = 0.0625
Question 11.
The experimental probability that Jason makes a free throw is 72%. If Jason shoots 50 free throws, about how many can you expect him to make? Explain.
Answer:
Given that,
The experimental probability that Jason makes a free throw is 72%.
The Jason shoots free throws = 50
Jason expects him to make = 72% x 50 = 36.